面向未知地形的四足机器人足端轨迹优化
柴 琦杨 杰
(青岛大学机电工程学院,青岛 266071)
不同于轮式或者履带式的传统机器人,足式机器人能够短暂的将腿抬离地面从而越过一些非连续性的障碍,可以在一些传统机器人难以到达的地方运动[1]。目前,一些机构正致力于研发性能优异的四足机器人。如,2004年美国波士顿动力公司研制了大型四足机器人Bigdog,展示了对于斜坡山地、松软雪地、光滑冰面等复杂地形的适应能力[2];Spot在Bigdog的技术基础上将液压驱动替换为电机驱动,配合机械臂,可以完成开门及上下楼梯等动作[3];麻省理工大学的MIT Cheetah3能够在没有视觉传感器的情况下攀爬楼梯[4];ANYbotics公司的ANYmal使用了集成的关节模块,降低功耗的同时提升了运动性能[5];国内宇树科技的Go1、云深处科技的“绝影”也在复杂环境的运动控制等方面展现出较好的性能[6]。随着四足机器人运动性能的提升,对四足机器人适应各种工作环境的要求也随之出现,机器人如何在未知环境中进行探索和移动成为研究热点。根据地形计算出四足机器人机身稳定角,以此实现机器人稳定行走,但增加了稳定角的求解难度[7];基于工作空间的中枢模式发生器(CPG)方法能够模仿动物在受到侧向冲击后的姿态调整,这种方法依赖机器人控制系统的快速性[8];虚拟模型方法可以对机器人的多个自由度进行解耦合控制,但是模型参数难以精确估计,导致仿真和实物测试差别较大[9];穷举法能够分析机器人的24种行走步态,针对不同的地形选择最合适的步态,但是此方法鲁棒性不强[10];利用传感器获取足端接触点的地形来调整机器人姿态的方法,不足之处在于只能探测接触过的地形,仍然要依赖机器人控制系统的快速性[11]。以上研究始终依靠四足机器人的快速反应和调整来适应未知地形对机器人的冲击,不能从根本上减小对机器人的冲击。为此,本文提出一种面向未知地形的四足机器人轨迹优化方法,将不同地形下的理想足端轨迹分段融合,得到适应多种地形的足端轨迹。
1 四足机器人受力分析
研究本体为斯坦福的四足机器人Doggo。Doggo采用并联式腿部结构,每条腿具有两个自由度,两个电机控制一条腿绕肩部转动,改变腿的等效角度和等效长度[12]。如图1所示,从足端到肩部的连线为并联腿的有效长度L0,L0与Z轴负向的夹角为φ,机器人腿部两个电机分别施加力矩τ1和τ2,足端与地面接触点的等效力为F,地面对足端的支撑力为N,地面对足端的摩擦力为f。地面与水平面之间的夹角为η

图1 支撑相足端受力分析

由式(1)可以得到足端的支撑力N

2 四足机器人轨迹规划
四足机器人常采用Trot(小跑)步态和Walk(行走)步态。Trot步态的过程如图2所示,首先左后腿HL和右前腿FR 一起迈出,半个迈步周期T之后,右后腿HR 和左前腿FL 再一起迈出。Walk步态按照FL-HR-FR-HL的顺序逐次迈步。
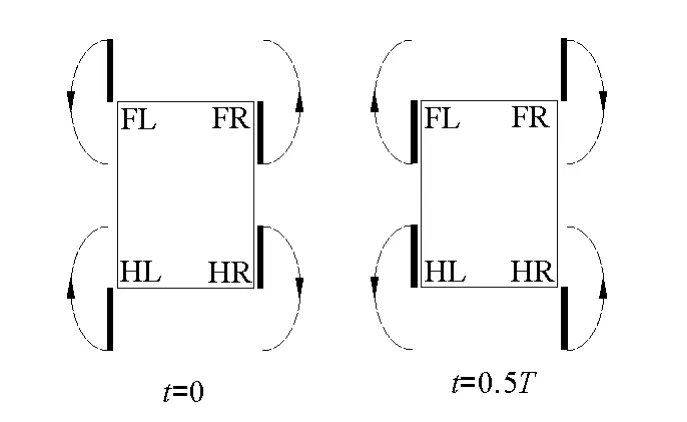
图2 四足机器人Trot步态迈步顺序图
2.1 足端轨迹规划及约束
如图3所示,机器人足端轨迹分为两部分:摆动相①,机器人足端处在悬空状态;支撑相②,足端与水平地面接触,支撑机器人做平行于地面的运动。四足机器人足端轨迹常采用摆线轨迹,摆线轨迹在摆动相①与支撑相②交替的位置速度和加速度都为零。从水平地面向上坡面过渡时,摆动相还未结束,足端速度未降到零便与上坡面接触,引起冲击;从水平地面向下坡面过渡时,支撑相方向与坡面方向不一样,也易引起冲击。
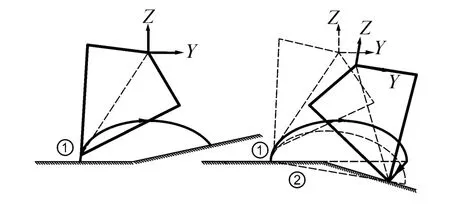
图3 摆线轨迹在上坡面和下坡面的运动情况
在坡面上为了实现摆动相①和支撑相②交替时速度和加速度为零,采用如图4所示方法,将支撑相足端轨迹调整到与坡面平行。为了减小机器人的足端在上坡面和下坡面所受的冲击,对图4中3种情况下的足端轨迹进行拟合,如图5所示,支撑相被分为向上坡面支撑相,水平支撑相和向下坡面支撑相3段,并得到机器人腿部轨迹在Y轴和Z轴上的约束。

图4 摆线轨迹在上坡面和下坡面的运动情况
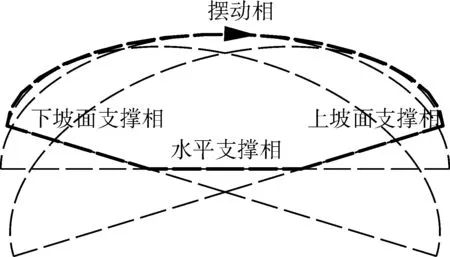
图5 分段摆线轨迹
Y方向位置约束

在此条件下,Y方向速度约束和加速度约束均为0。
Z方向位置约束

在此条件下,Z方向速度约束和加速度约束均为0。
2.2 足端轨迹函数
对式(3)、式(4)求解,得到足端轨迹方程
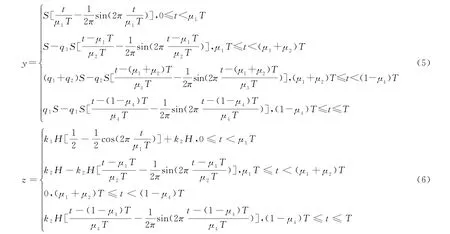
其中,μ1,μ2,μ3,μ4分别为摆动相、向上坡面支撑相、水平支撑相和向下坡面支撑相在迈步周期T中的占比,k1,k2分别为摆动相和支撑相在Z方向移动距离占迈步高度H的比例,q1,q2,q3分别为向上坡面支撑相、水平支撑相和向下坡面支撑相在Y轴方向上移动距离占迈步总长S的比例。
3 机器人实物测试
为了验证足端轨迹优化的有效性,由Doggo完成实验验证。如图6所示,Doggo由8个无刷电机驱动,躯干装有惯性测量元件BNO080 IMU。

图6 斯坦福Doggo机器人外观
机器人的腿部结构参数见表1,机器人足端轨迹参数见表2。测试地形:水平地面,水平地面向上坡面过渡和向下坡面过渡3种;测试步态:Trot和Walk,记录机器人分别采用摆线轨迹和分段摆线轨迹在行进过程中俯仰角pitch和横滚角roll的变化,以及每条腿两个电机的交轴电流之和表征足端力矩。

表1 四足机器人腿部结构参数
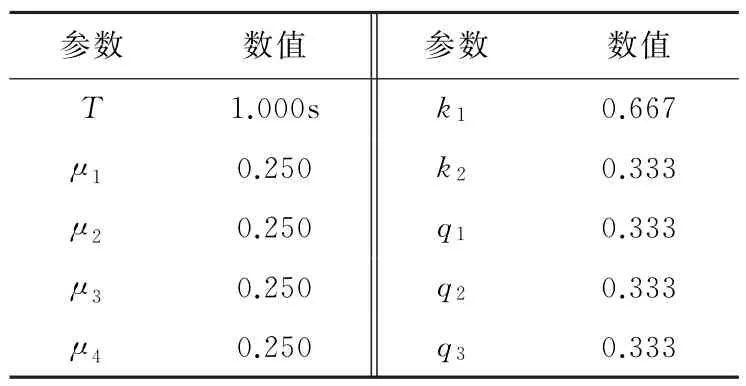
表2 机器人足端轨迹参数
3.1 面向平坦地形的行走测试
Doggo在水平地面上分别使用Trot和Walk步态启动并行走一段距离,记录机器人躯干的pitch俯仰角和roll横滚角的角度变化。由图7可知,Trot步态下采用分段摆线轨迹,行进过程中pitch角和roll角的幅值减小,运动稳定性提高。由图8可知,在Walk步态下采用分段摆线轨迹,机器人行走过程中pitch角幅值减小,但roll角幅值未减小,运动稳定性改善程度不如Trot步态。
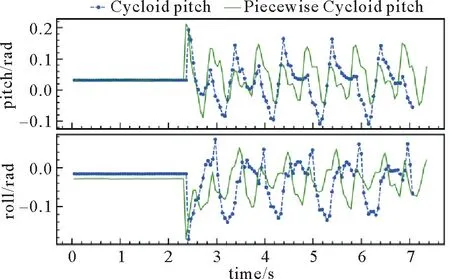
图7 Trot步态下机器人在水平地面pitch和roll角

图8 Walk步态下机器人在水平地面pitch和roll角
如图9和图10所示,采用分段摆线轨迹,Trot步态和Walk步态下在水平地面上运动时机器人足端力矩减小,但Walk步态的足端力矩幅值比Trot的大。
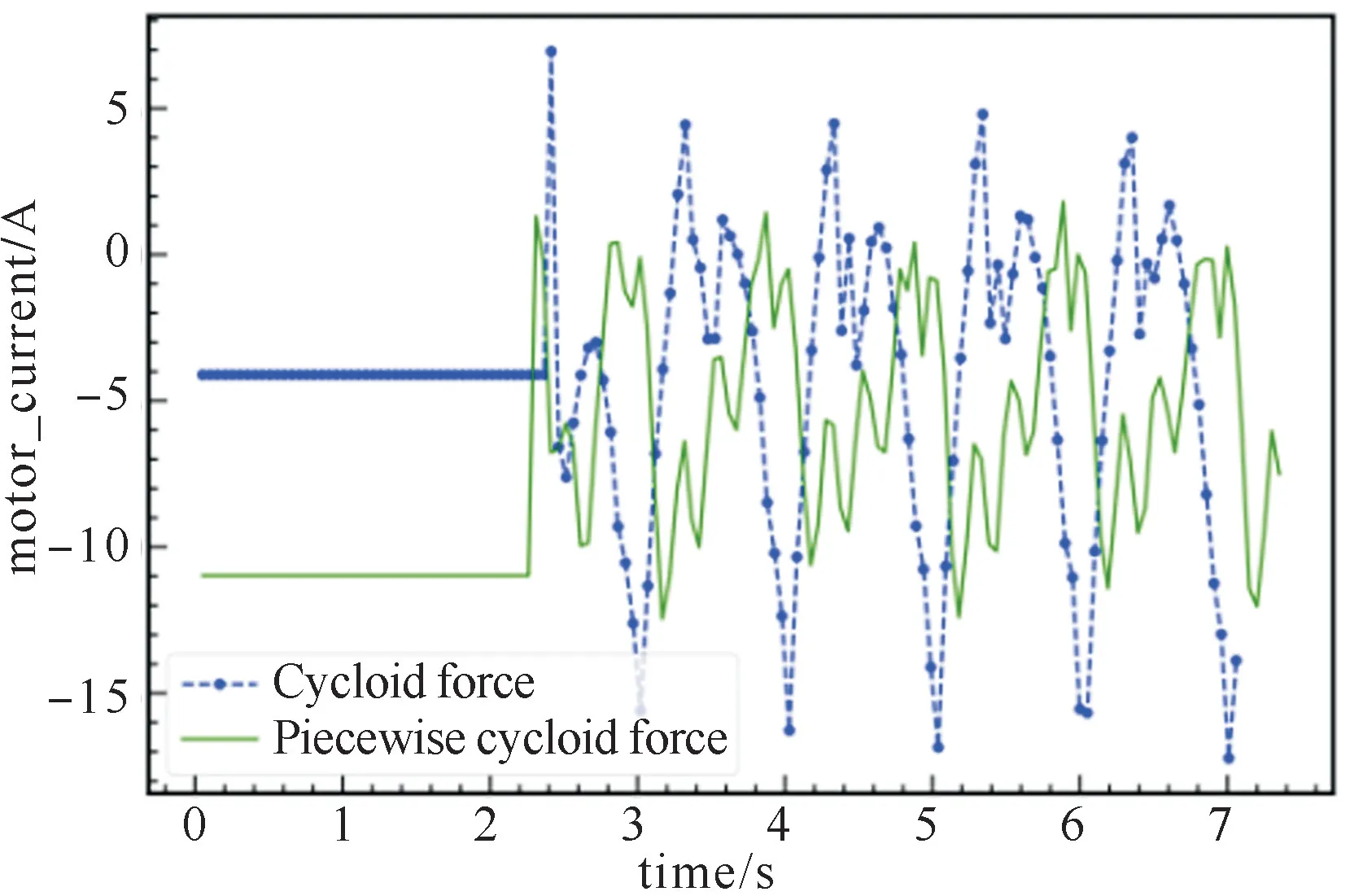
图9 Trot步态下机器人在水平地面的足端力矩
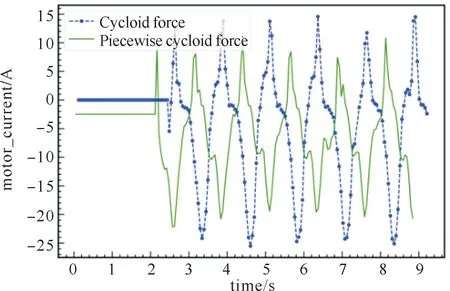
图10 Walk步态下机器人在水平地面的足端力矩
3.2 上坡面地形的行走测试
Doggo从水平地面启动走到上坡面,记录机器人的pitch和roll角度变化。由图11和图12可知,采用Trot步态上坡时,分段摆线轨迹没有对机器人的pitch和roll角幅值产生改善的效果,采用Walk步态上坡时,分段摆线轨迹减小了pitch角和roll角的幅值,如图13所示。
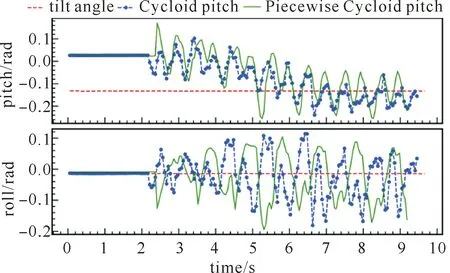
图11 Trot步态下机器人在7.6°上坡面pitch和roll角
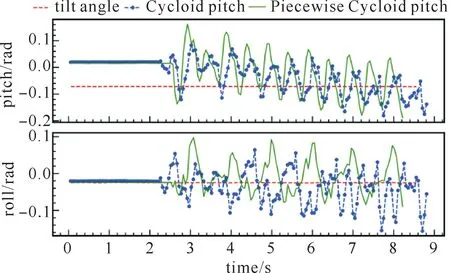
图12 Trot步态下机器人在4.0°上坡面pitch和roll角
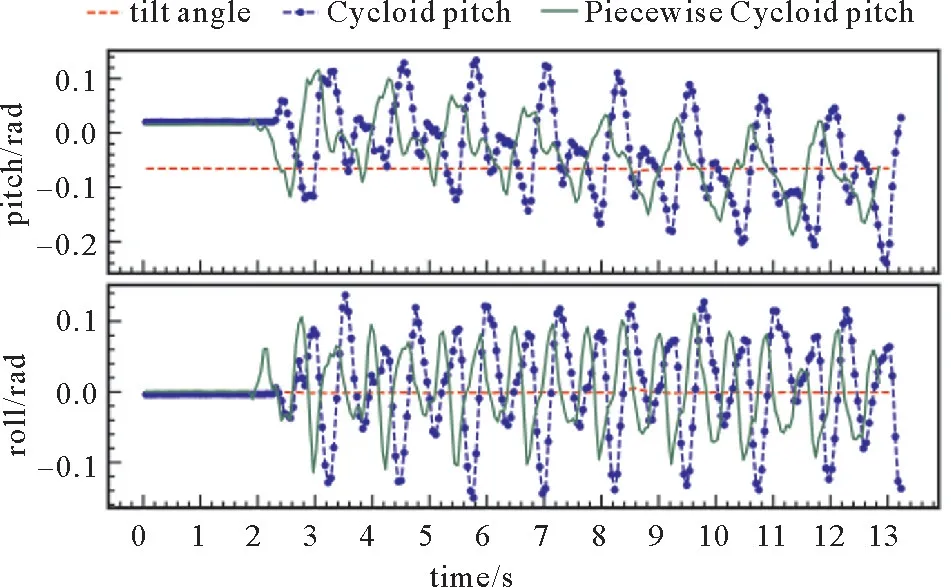
图13 Walk步态下机器人在3.8°上坡面pitch和roll角
两种步态下,Doggo足端力矩在行进过程中的变化情况见图14和图15。采用分段摆线轨迹,Trot步态和Walk步态下,足端力矩的幅值均减小。Trot步态在4°上坡面的足端力矩幅值比7.6°上坡面的足端力矩小,Walk步态的足端力矩幅值比Trot步态的足端力矩大。上坡时,随着坡度增大,四足机器人足端力矩增大。Walk步态由于支撑相的三条腿足端速度不一致,产生了额外的力矩,3.8°坡度下足端力矩比4.0°坡度下Trot步态的足端力矩大。

图14 Trot步态下机器人在4.0°和7.6°上坡面的足端力矩

图15 Walk步态下机器人在3.8°上坡面的足端力矩
3.3 下坡面地形的行走测试
Doggo从水平地面启动走到下坡面的过程中,记录pitch和roll角度变化情况。由图16可知,采用分段摆线轨迹,Trot步态下坡时,机器人的roll角幅值未减小。由图17可知,pitch角以更小的幅值向斜面角度靠拢,运动稳定性得到改善。由图18可知,采用Walk步态下坡时,在分段摆线轨迹下,pitch角的幅值均减小,运动稳定性改善程度不如Trot步态。

图16 Trot步态机器人在5.3°下坡面pitch和roll角
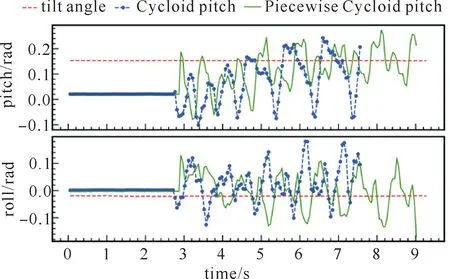
图17 Trot步态机器人在8.7°下坡面pitch和roll角
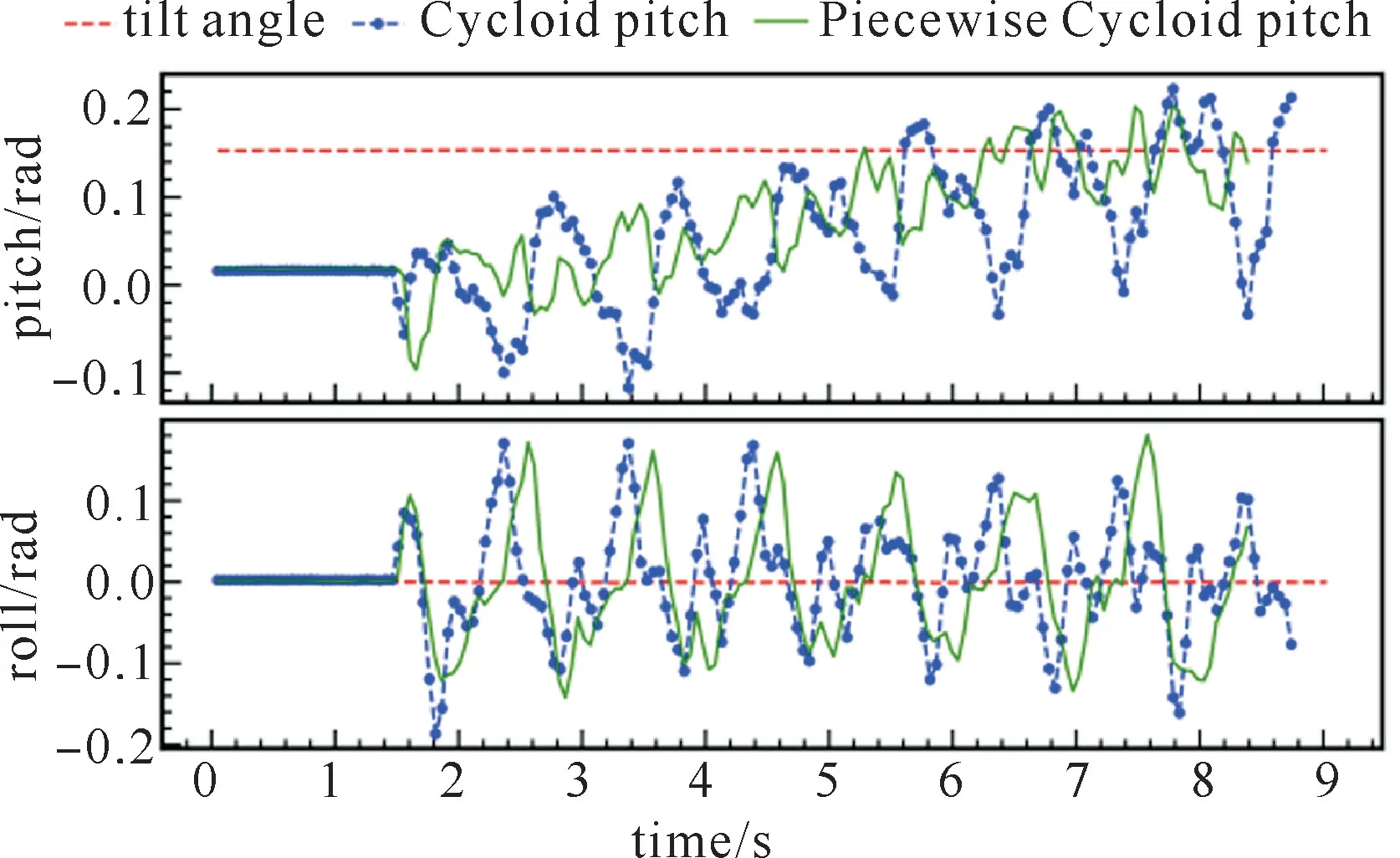
图18 Walk步态机器人在8.7°下坡面pitch和roll角
采用分段摆线轨迹后,机器人采用Trot步态和Walk步态下坡时足端力矩幅值均减小,如图19、20所示。Trot步态5.3°上坡面的足端力矩幅值比8.7°上坡面的足端力矩小,Walk步态的足端力矩幅值大于Trot步态的足端力矩。下坡时,随着坡度增大,四足机器人足端力矩增大。相同坡度下Walk步态由于支撑相的三条腿足端速度不一致,产生了额外的力矩,足端力矩比Trot步态大。
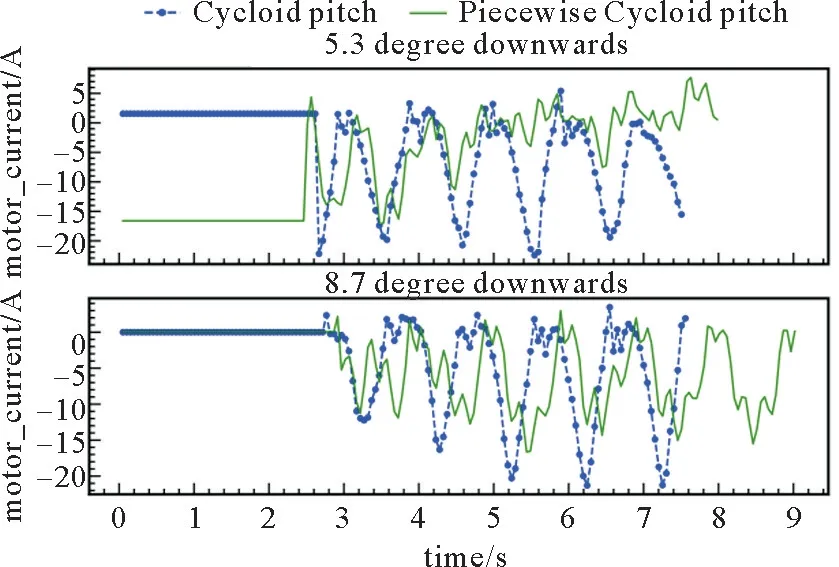
图19 Trot步态下机器人在5.3°和8.7°下坡面足端力矩
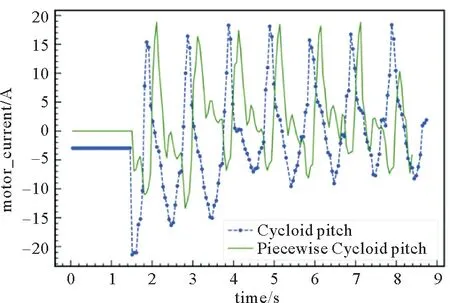
图20 Walk步态下机器人在8.7°下坡面足端力矩
4 结论
四足机器人常采用快速调整的方法减弱地面冲击对机器人平衡的影响,本文提出的优化算法对三种地形下的理想足端轨迹进行分段融合,能够直接减少足端的地面冲击,提高稳定性。但是分段后轨迹的复杂程度提高,给机器人引入了额外的不稳定性;而且固定的轨迹不能对所有地形都保持较高的契合度。如果能够结合快速调整的优势,则对未知地形将有更好的适应性。

