回归定义 灵活解题——以椭圆的定义为例

包正峰 (江苏省梅村高级中学 214112)

椭圆的定义最初是从一种形象直观的操作来引导学生认识椭圆的,随着对椭圆的逐步理解,学生对定义就会有新的认识.本文从不同角度的题型展开,帮助学生深度理解椭圆的定义,实现知识的有效迁移．

1 借助椭圆定义简化运算过程

数学概念高度凝结着数学家的思维,是数学地认识事物的思想精华,是数学家智慧的结晶,蕴涵了最丰富的创新教育素材．

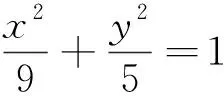
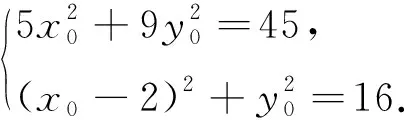
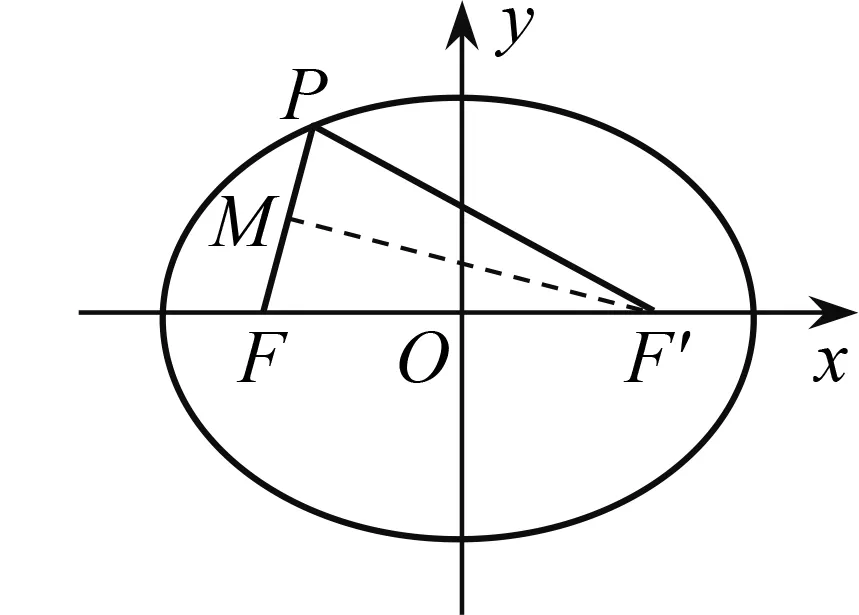
图1

在理解椭圆的定义时,不但要清楚椭圆定义的文字表述,还要注意其代数表征．在深入理解定义后,便可选择合理的运算思路,缩简运算过程．利用椭圆的定义解答此题,就会发现“柳暗花明又一村”．

2 利用椭圆定义提升空间想象能力

波利亚认为“回到定义上去是一项重要的思维活动”[1],并将这一重要的思维活动列在解题的显著位置加以阐述．椭圆的定义体现了椭圆的本质属性,是椭圆中最活跃的元素．运用椭圆的定义解题是一种最直接、最本质的方法,有时可以收到立竿见影之效．

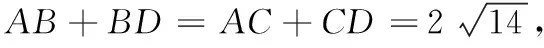
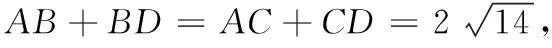
图2

把椭圆的定义从平面延伸到空间,考查学生对数学基本概念的深度理解．本题以椭圆定义为方向,让人耳目一新．理解定义的丰富内涵,是学生应经历的重要过程．

3 运用椭圆定义优化向量运算方法

椭圆的定义与平面向量的结合,可以组成美妙绝伦的数学问题．这类问题对数学核心素养的要求较高,既要有强大的向量运算能力、数学推理作支撑,又要有几何直观统领全局．

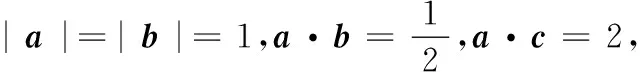
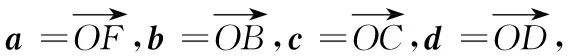
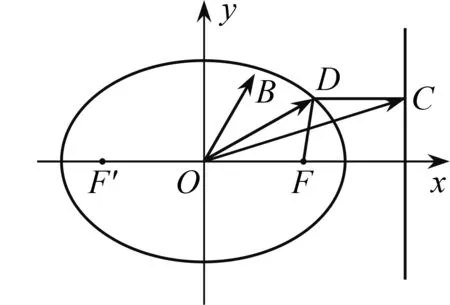
图3

解析几何是沟通代数与几何的桥梁,是培养学生数形结合意识的重要素材．而解析几何中的椭圆性质与结论众多,题型灵活多变,且题目计算繁琐,其中椭圆的定义又是解析几何教学的重点,是曲线方程、几何性质及其应用的基础.因此在求解椭圆有关问题时,必须重视椭圆的定义在解题中的应用．只有正确对待定义、认真学好定义、恰当合理地回归定义,才能够提高学生的解题能力,帮助学生形成良好的数学思维习惯．