一道直线过定点试题的探究与拓展

汤 琴 (江苏省姜堰中学 225500)

在一次测试中,我们遇到一道直线过定点的问题,题目看上去并不难,但是学生做下来的情况并不好.从学生的答题过程来看,方法偏繁、运算量大,以及对未知变量的范围控制不准确,导致出现各种错误．解决这道解析几何题的基本思路是运用解析法解决问题,这也是大多数学生选择的方法．在通性通法比较繁的情况下,我们希望学生能够认真分析条件,从多个角度思考问题,选择更加优化的解法解决问题．

1 试题

如图1,平面直角坐标系内,O为坐标原点,点A在x轴正半轴上,点B在第一象限内,∠AOB=60°．

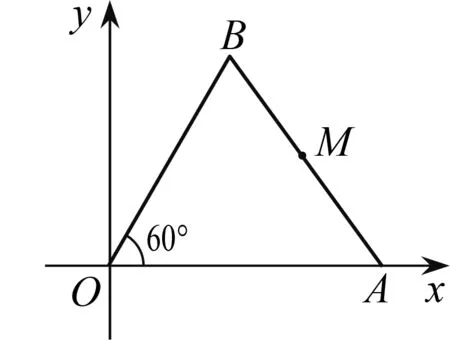
图1

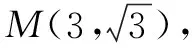
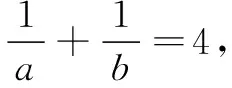
2 解法

先考虑第(1)题．

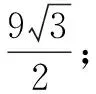
评价常规做法容易想到,但是运算量大,比较繁琐,耗时长．

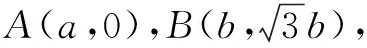
评价向量是沟通代数和几何的桥梁,这个方法灵活建立了a,b间的关系,简化了运算,很棒!

在实际解题过程中,设线和设点是解析几何中最常用的两种设法,因此大部分学生选择了解法1或者解法2,但在这些学生中只有不到一半最终得到了正确的结果．这暴露了部分学生的运算能力存在问题．

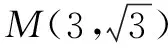
图2

评价对平面图形进行分割,运用相似建立变量间的关系,引导学生对新出现的两个变量的关系进行研究,激活学生思维．

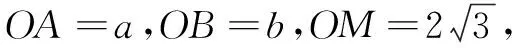
评价妙!善于观察图形的位置关系,直观想象能力较强.借助等面积法建立变量之间的关系,是一种非常有创新的想法．

下面考虑第(2)题．

评价常规方法,根据题意写出两个点的坐标,表示出直线方程,求出直线过定点．

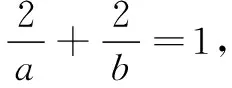
评价关注问题间的关联,找到突破口,运用向量中的共线解决问题．

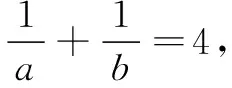
3 拓展

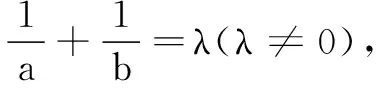
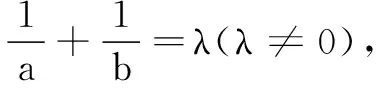
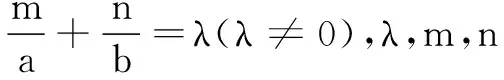
4 启示

从这道题的解答过程可以看出,学生的思维层次大概分为三层:第一层次,在直角坐标系中很容易想到的是设点或者设直线方程,运用解析法解决问题;第二层次,观察到题目中有三角形,有边长,有角度,会联想到解三角形的方法,联想到向量的三点共线;第三层次,对研究过程中的思想方法进行迁移,拓展出其他结论．显然,第一个层次是大多数学生都能想到的,第二层次则体现了学生对知识的融会贯通,第三层次体现了学生的自主学习迁移的能力．

数学解题过程是一个思维过程,是一个把知识与问题联系起来思考、分析、探索的过程[1]．在数学教学过程中,我们要教给学生如何思考问题,如何将问题深化,如何挖掘数学问题的本质．