初中数学实验常态化实施的三个着力点*

许 彬 (江苏省苏州中学园区校 215021)

数学实验是以“做”为支架的教学方式,学生通过“做”数学,出色达成知识、能力及素养目标．江苏省自2001年在义务教育初中数学教科书中设置“数学实验室”栏目起,省中小学教学研究室就开启了初中数学实验的理论研究与实践探索．多年来,经过大批名特优教师、科研人员、高校教授等的不懈论证及系统实践检验,目前已经形成了较为完善的数学实验理论体系和课程资源,这些都为初中数学实验常态化提供了实施保障．初中数学教师只有将数学实验推向常态化,才能体现出教与学方式转变带来的最优效益,只有找准数学实验常态化实施的着力点,才能高质量地实现数学学科立德树人的育人价值．

1 立足点:精准掌握初中数学实验手册内容,常态化实施的资源保证

为了指导教师开展数学实验教学,帮助初中生做数学实验,2014年经江苏省中小学教材审定委员会审查通过了《义务教育教科书·数学实验手册》(下称《手册》):一方面将教科书中的数学内容直观化、具体化、可操作化,方便师生在课堂教学过程中使用;另一方面根据知识学习需求,系统地开发和设计了部分数学实验,并提供实验所需材料,如图形纸片、透明纸、方格纸等,方便实验教学实施．《手册》为师生提供了系统的数学实验资源,是数学实验常态化的实施保障,所以教师要精准掌握《手册》内容．

《手册》共5册,合计82个实验主题.七年级侧重于“游戏、调查、制作”,八年级侧重于“调查、制作、设计”,九年级侧重于“制作、设计、课题研究”．常态化实施数学实验的有效做法就是要整合教材内容与《手册》的实验资源,将实验有效地融入到课堂教学中去．《手册》中的实验资源可分为“片段型”(或“融入型”)和“专题型”两类．片段型实验可作为课堂的某个教学环节,如教学情境、观察猜想、结论验证等;专题型实验一般会有明确的主题和完整的实验过程,往往作为一个教时．

从数学实验目的看,可以分为:实物验证型、实物理解型、实物探究型、计算机探究型、计算机验证型、计算机理解型．例如,抢“十七”游戏(实物探究型)、打印纸中的数学(实物理解型)、折叠与轴对称(实物验证型)、一次函数图象(计算机探究型)、模拟体彩开奖(计算机理解型)、垂线段最短(计算机验证型)．

《手册》中的数学实验内容均对应指向学生的关键能力或素养,如“键盘中字母排列的奥秘”指向数据分析观念,“数格点,算面积”指向符号意识、推理能力,“探究无盖纸盒的最大容积”指向模型思想,“找重心”指向运算能力,“折纸与特殊角的三角函数”指向几何直观,“剪纸与中心对称图案”指向空间观念,“打印纸中的数学”指向数感、运算能力,“翻牌游戏”指向推理能力、应用意识．数学实验使学生真正成为学习活动的主人,通过操作实践,经历实验过程,挖掘实验活动的内隐性知识,学会数学化思考,很好地落实了课标的基本理念．

82个数学实验主题对应“数与代数”“图形与几何”“统计与概率”领域情况如表1所示．

表1 数学实验在各个领域的分布设置情况

《手册》是学生学习的辅助用书,具有实践性、适应性,作为重要的教学资源,具有目标性、科学性,给数学学习提供了观察现象、动手实践、分析思考的途径,是引导学生发现、分析、思考、理解、掌握、解决数学问题的重要文本资源．它改变了教师“教”和学生“学”的方式,充分理解和掌握其内容并准确把握每个数学实验目标是使用者的首要任务．

2 生长点:精心构建数学实验常态化教学范式,常态化实施的教学路径

数学实验教学是推动做数学常态化实施的最有力手段．它以数学问题为出发点,以获得数学结论为目标,从直观现象出发去发现和猜想,给出验证和理论证明,是学生亲历数学知识建构的实践活动．

数学实验教学过程是在教师的指导下设计 研究步骤,通过对工具的操作,发现规律,提出猜想,对数学结果进行验证或证明．根据数学实验任务及实施途径,构建出验证型、理解型和探究型 这三种数学实验教学范式,具体教学实施流程如 图1～3所示．

图1 验证型数学实验教学流程

图2 理解型数学实验教学流程

图3 探索型数学实验教学流程

案例1实验主题:“做”菱形．

教学目标:通过剪、叠、折的方法制作菱形,深度理解菱形的判定方法．

实验工具:剪刀、等宽矩形纸片若干张,任意三角形纸片1张,毛边纸1张．

教学设计:

·剪菱形

(1)猜猜老师手中的四边形纸片是菱形吗?如何验证?

(2)给你一张矩形纸片,你能剪出一个菱形吗?请向同学展示你的剪法并说明为什么是菱形.

·叠菱形

(1)取出两张等宽的矩形纸片,将其非重合地叠在一起,观察重叠部分是什么特殊四边形,证明你的猜想．

(2)转动其中一张纸片,观察重叠部分的面积何时最小何时最大,你有什么发现?

·折菱形

(1)利用一张矩形纸片能折出菱形吗?交流你的折法并证明．

(2)用三角形纸片能折出菱形吗?展示你的折法并予以说理证明．

(3)用毛边纸能折出菱形吗?请展示折法并给出证明．

评析波利亚指出:“抽象的道理很重要,但是要用一切办法使它们看得见、摸得着．”如何判定一个四边形是菱形?教材通常以文字来表征,即呈现定义或定理,多数学生仅停留于感性了解,数学实验教学能够以做实验的方式引领学生深入理解知识．“剪菱形”中的“猜”就是让学生根据纸片特征结合菱形定义作出判定,“剪”是将定义判定法用于实践活动,把抽象的文字表述落实到“做”之中．“叠菱形”需要运用菱形的定义、面积以及与矩形之间关系等知识,使学生对菱形的理解立体化．“折菱形”目的是理解菱形的判定定理,学生需要根据手中纸片的不同形状、不同条件,灵活选择判定定理,怎样折?为什么这样折?具象的实验活动唤起学生操作和说理的热情．本实验教学过程具有层次性、开放性,能够满足学生动手动脑做数学的逻辑需求和心理需求,充分体现了学生的主体性．在做菱形的实验中,学生对菱形判定方法的理解从表象到实质、从操作到说理、从合情推理到演绎论证,积累了数学活动经验,情感、态度、价值观得到体验与获得．

3 发展点:精确提升核心素养实现立德树人,常态化实施的育人价值

初中数学实验课程是国家课程的补充和辅助课程,对国家课程的学习起到有效的促进作用,承载着良好的学科育人功能．初中数学实验紧扣《义务教育数学课程标准(2022年版)》主旨,以常态化实施的方式精确有效地提升学生的数学核心素养,形成数学学习能力,使他们会用数学的眼光观察世界、会用数学思维思考世界、会用数学语言表达世界[1]．

案例2实验主题:打印纸中的数学．

实验目的:通过对A4打印纸长与宽比值的猜测、计算、折叠等实验活动,探索A4打印纸长与宽的比值,感受无理数的存在性．

实验准备:A4打印纸、A3纸、刻度尺、计算器．

实验过程:

活动1 猜一猜,算一算．

(1)呈现A4纸,并提问:你打算研究A4纸的哪方面的问题?你能猜出A4纸的长与宽之比是多少吗?

(2)度量:利用刻度尺度量A4纸的长与宽,计算长与宽的比值,结果精确到0.01．

活动2 折一折,证一证．

(1)按如图4 (1)(2)的方式折叠A4纸,你能得到什么样的结论?

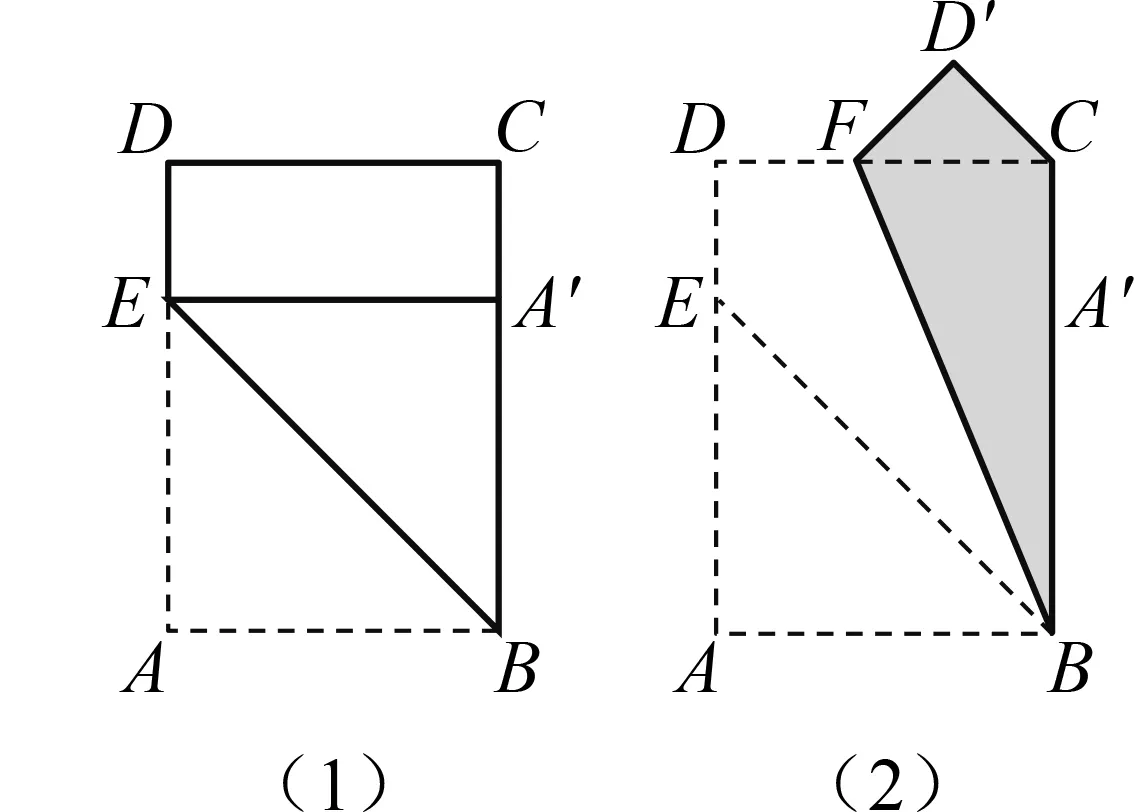
图4

(2)在折叠的基础上,根据折痕计算A4纸的长与宽之比．

(3)如图5(1) (2),将A4纸的∠ABC,∠DCB对折,折痕交于点O,再翻折AB与OB重合,计算边BC与AB的比值．

图5

活动3 思一思,想一想．

(1)请研究:A3纸的长与宽之比是多少?A3纸与A4纸的关系是什么?

(2)如何制作A5纸呢?你的根据是什么?

(3)怎样制作A2纸、A1纸、A0纸?思考:字母A后缀数字与纸张大小或者裁剪次数是何种关系?你知道A0纸的面积是多少吗?

(4)联想:为什么电脑显示器设计成16∶9呢?猜想电影幕布的尺寸,并说说你的思考．

活动4 拓展与迁移．

生活中除了A型纸还有B型、K型纸,请探究其长与宽之比,并写出过程．

评析数学实验的育人价值就是帮助学生形成和发展核心素养,通过学科学习逐步形成“正确的价值观、必备品格和关键能力”[2]．本案中,学生对A4打印纸的研究从“目测”到“度量”再到“折叠”最后到“说理证明”,数学思维从低级走向高级,认知也从感性上升至理性.数学实验带领学生亲历知识生成,感受无理数的真实存在性．学生能将A4纸的研究经验迁移到对整个A系列纸的研究,研究策略得到升华.这样做不仅训练了学生的数学思维,还提高了数学实践能力,学生在数学实验活动中获得知识,数学抽象、逻辑推理、数学建模等核心素养得到有效提升．既然A型纸的长宽之间具有某种性质,那么生活中的K型、B型纸呢?拓展活动将知识、经验、方法、思维的要求推向了更高层次,很好地培养了学生的应用意识和创新能力．数学实验让学生享受到完整的数学学习过程,能培养学生勇于探索的精神以及求真务实的学习态度,对学会学习产生深远的影响．

初中数学实验常态化实施让学生动手“做”数学、动脑“思”数学,在数学实验中发现问题、验证(证伪或证实)知识、形成数学能力.积累基本活动经验,学生经历知识“怎么来?”“是什么?” “到哪里去?”的完整过程.在这一过程中,数学实验承载着促进认知、激发情感、启迪智慧、塑造品格的功能,对提高数学学习兴趣,发展学生数学核心素养,实现从学科教学走向学科育人,有直接推动作用．