数学文化中的建筑蓝图——与建筑有关的高考试题赏析

沈丹丹 (江苏省无锡市东北塘中学 214191)

安恺凯 (江苏省天一中学 214101)

建筑是根据美感和功能的需求,对土地、材料、结构通过精密的数学计算进行设计的．当人们徜徉在人类建筑的长廊中流连忘返、被震撼的时候,应该知道这些建筑与数学的发展密不可分．新高考重视体现数学的科学价值、应用价值、文化价值和审美价值.建筑作为屹立着的“凝固的数学”,作为抽象的数学在现实中形象化的典型,逐渐成为新高考命题的热门情境载体．下面结合近几年高考与联考中的数学文化题赏析之．

1 举架结构——建模来解举步比

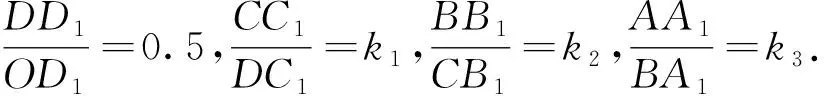
A．0.75 B．0.8 C．0.85 D．0.9

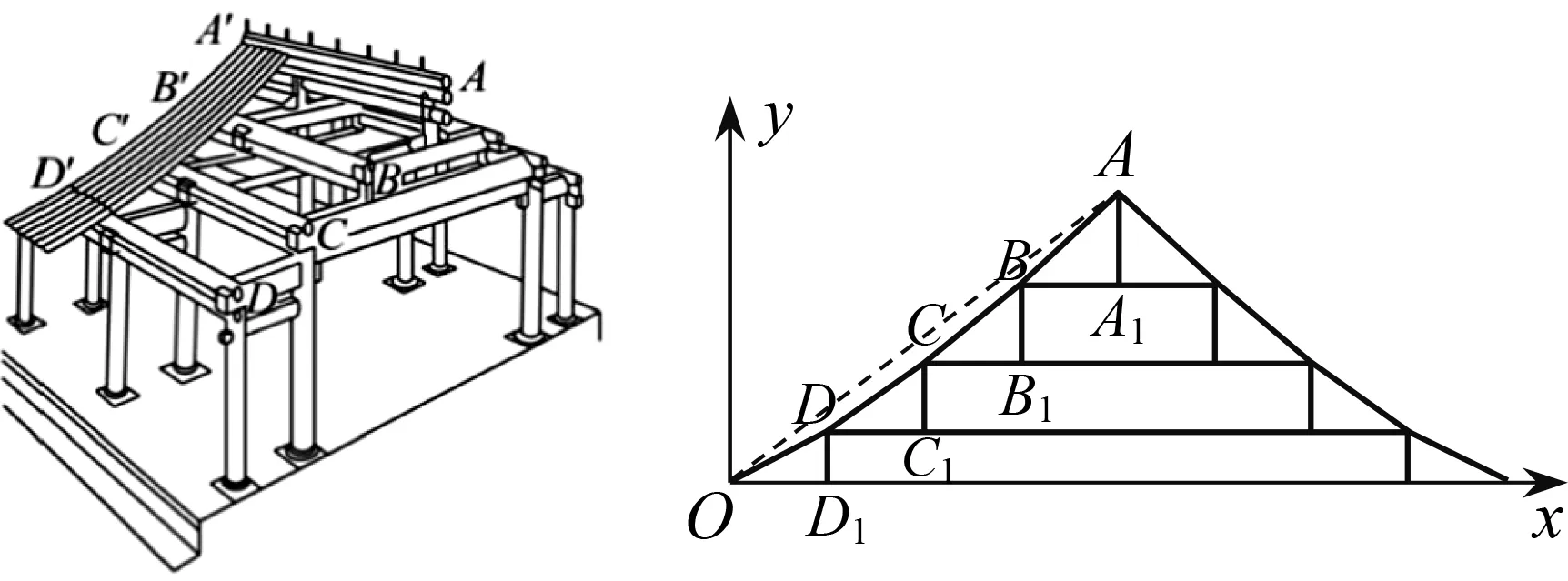
图1 图2

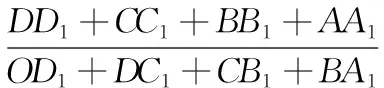
背景赏析举架结构是中国古代建筑确定屋顶曲面曲度的方法,这种建筑在梁架层叠加高时,用举架方法使屋顶的坡度越往上越陡,从而呈凹曲面,以利于屋面排水和檐下采光,形成中国古代建筑独有的风貌．本题将举架结构图抽象得到数学几何图形,考查学生的阅读理解能力和数学建模能力．中国古代建筑独树一帜,其成果在世界建筑史上具有重要地位,试题设置相关情境对引导学生关注我国古代优秀成果、增强民族自信心具有积极的教育意义．

2 著名斜塔——三角函数话倾斜

例2(2022年台湾地区学测B考科第19题)瘦长的塔因为年代久远,塔身容易倾斜(图3)．在图4中,以粗黑线条代表塔身,而塔身的长度称为塔高,塔身与铅直虚线的夹角θ称为该塔的倾斜度(0≤θ<90°),又塔顶至铅直虚线的距离称为该塔的偏移距离．

图3 图4

(1)中国虎丘塔、护珠塔与意大利的比萨斜塔是三座著名斜塔,它们的塔高分别为48,19与57(公尺),偏移距离分别为2.3,2.3与4(公尺),塔的倾斜度分别记为θ1,θ2与θ3,试比较θ1,θ2与θ3三数的大小关系．

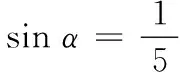
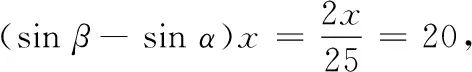
背景赏析意大利的比萨斜塔是世界斜塔中最知名的一座,而在中国很多地方也有斜塔．上海天马山山顶的护珠塔,建于北宋元丰二年,早于比萨斜塔94年建造.从题中可以看出护珠塔的倾斜度甚至超过比萨斜塔．苏州的虎丘塔建造的年代则更加久远,建于五代后周显德六年,至今已有一千多年,同时也比护珠塔更加高大雄伟,成为苏州古城的标志.宋代文人苏东坡曾说过:“到苏州而不游虎丘,乃憾事也．”本题从数学的视角对不同地域、不同时期的建筑进行对比研究,彰显出建筑艺术超越时间、空间、文化的审美趋同．

3 北京天坛——数列性质环中藏

例3(2020年新课标II卷(理科)第4题)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )．

图5

A．3 699块 B．3 474块

C．3 402块 D．3 339块

背景赏析圜丘坛为露天三层圆形,象征天．中国古人把一、三、五、七、九单数称为“阳数”,又叫“天数”,而九则是阳数之极．因此,圜丘的层数、台面的直径、墁砌的石块、四周的栏板均用天数,表示天体至高至大．圜丘最高一层台面直径是九丈,名“一九”;中间一层十五丈,名“三五”;最下一层二十一丈,名“三七”．站在台面中央的天心石上高呼,回音很大,好似一呼百应．据声学专家揭秘,从发音到声波再回到圆心石的时间仅为0.07秒,说话者根本无法分清它是原音还是回声,所以有一呼百应的感觉．圜丘坛是中国古人的宇宙哲学观通过数学知识蕴含在建筑中的典范,同时也反映出中国古人在数学、声学、建筑学上的非凡智慧．

4 十字歇山——立体几何巧组合

例4(2022年天津高考卷第8题)如图6,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120°,腰为3的等腰三角形,则该几何体的体积为( )．

A．23 B．24 C．26 D．27

图6

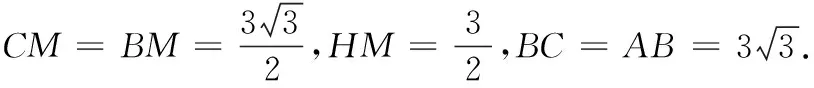
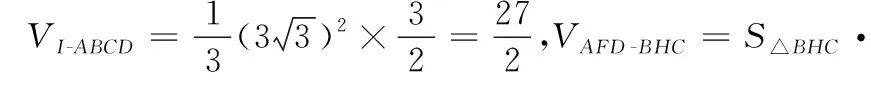
背景赏析中国古建筑屋顶的几何形态千变万化、瑰丽多姿,不同几何体的相互组合、穿插,又会形成不同的屋顶形式．十字歇山顶是由两个歇山顶呈90°垂直相交而成,从空中看屋顶平面像一个十字形,形成的四个山面都是歇山式,四个山花朝外,建筑立面从而更加丰富,造型也更加美观.目前留存的比较有代表性的便是题中图6左图中的北京故宫的角楼．建筑设计要运用结构理论,体现出技术与艺术的完美结合,而结构理论的运用,需要借助于大量的数学模型与几何知识,正如本题中的十字歇山顶．

5 大兴机场——欧拉公式道曲率

图7

(1)求四棱锥的总曲率;

(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数．

解析 (1)因为四棱锥有5个顶点,5个面,其中四个侧面是三角形,一个底面是四边形,所以四棱锥的总曲率为5×2π-4π-2π=4π．

背景赏析在传统建筑行业,几乎所有的作品都是横梁、立柱、平墙、方窗,泾渭分明．换言之,几乎所有的建筑表面都是平直的．大兴国际机场在建筑结构上却有很多光滑的曲线,仰望穹顶,航站楼屋顶的钢架结构,被两簇彼此垂直的曲线结构剖分,和谐优雅,流畅灵动．如此优美的形态在几何学中对应着一个非常深刻的数学几何概念——黎曼叶状结构．数学的发展让建筑大师的伟大构想得以实现,在建筑中更能窥见数学应用的奥妙玄机．

上述几例阐明了建筑作为人类栖居与活动的主要场所,从古代的石木结构,到现在的高科技建筑,都蕴含着许多数学奥秘．期待随着数学的不断发展,建筑在数学的启发下能有更多的表现形式,为世界创造出更多令人叹为观止的美．