(1+1)维Maxwell-Chern-Simons-Higgs系统解的整体存在性
周羽, 金艳
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
1990年,Lee等[1]提出了如下Maxwell-Chern-Simons-Higgs(MCSH)自对偶模型:
(1)

1 降维系统
设(1+2)维MCSH系统(式(1))与变量x2无关.于是将式(1)中的符号A2替换为B可得如下(1+1)维MCSH系统:
(2)
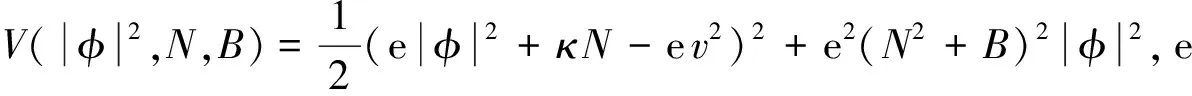
在以下研究中,本文用重复指标表示求和记号,用C表示各种常量(研究系统解的局部性质时可假设T≤1,由此此时可用C代替光滑函数C(T)),用AB表示估计A≤CB,用Hs≡Hs(R)表示Sobolev空间Ws,2(R),并记L2(R)≡H0.定义通常意义下的规范场强和协变导数分别为:
(3)
定义通常意义下的规范变换为:
φ→φ′=e-ieχφ,Aμ→A′μ=Aμ+∂μχ,Dμ→D′μ= ∂μ-ieA′μ,
(4)
其中χ:R1+2→R是光滑函数.根据酉群定义知e-ieχ∈U(1)={e-iα|α∈R}.将式(4)代入式(2)计算可知,拉格朗日密度(2)在规范变换下保持不变.利用变分法对式(1)进行计算得与其对应的Euler-Lagrange方程为:
(5)
(6)

(7)

(8)
(9)
根据式(5)—(9)构造的(1+1)维MCSH系统所对应的守恒能量函数为:
(10)
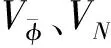
1)非拓扑边界条件:(φ,N,Aμ,B)→(0,ev2/κ,0,0), |x|→∞.


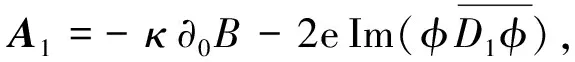

(11)

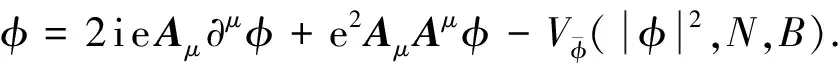
上述柯西问题对应的初始数据为:
(12)
上述柯西问题应满足的约束方程为:
(13)
2 主要结果及其证明
2.1 预备知识
为便于计算,本文取Chern-Simons耦合常数κ= 1.

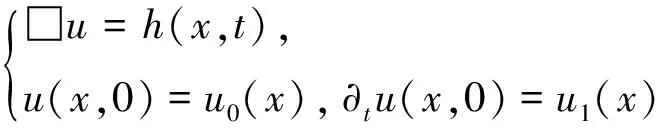
2.2 解的整体存在性及其证明
定理1设初始数据(12)的存在空间为φ0∈H2,φ1∈H1,a0μ∈H2,a1μ∈H1,b0∈H2,b1∈H1,n0∈H2,n1∈H1,且该初始数据满足约束条件(13),则系统(11)—(12)存在唯一的整体解,且该解满足φ,Aμ,B,N∈C([0,∞),H2(R))∩C1([0,∞),H1(R)).
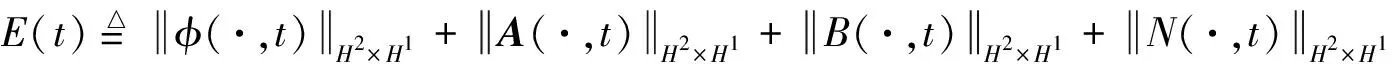



由上式进一步可得∂μφ的L2-范数估计为:


用协变导数算符D1作用于式(9)的两端可得:
(14)

由上式可得DμD1φ的L2-范数估计为:
3 系统所对应的能量函数守恒的验证
为验证能量函数E(t)关于时间是守恒的,本文对E(t)关于t求偏导数后再结合式(6)—(9)进行计算得:


