一类时间-空间分数阶Klein-Gordon方程的孤立波解

陆求赐, 王学彬, 张宋传, 徐瑞标

( 1.武夷学院 人文与教师教育学院, 福建 武夷山 354300;2.武夷学院 数学与计算机学院, 福建 武夷山 354300 )

0 引言

由于分数阶Klein-Gordon偏微分方程在流体力学、电学、信号处理、系统辨识以及经济学等领域有着广泛的应用[1-2],因此寻求分数阶Klein-Gordon方程的解具有重要意义.本文考虑如下一类时间-空间分数阶Klein-Gordon方程的孤立波解:

(1)

其中x∈Rn,n∈Z+,t>0, 0<α≤1,d,e∈R为参数.

式(1)是一类重要的分数阶偏微分方程(薛定谔方程的一种相对论形式),最初是由瑞典理论物理学家O.Klein和德国物理学家W.Gordon分别独立推导得出的[3].在式(1)中当α=1时,式(1)为整数阶Klein-Gordon方程[4].目前,已经有很多学者借助不同的求解方法对方程(1)或与其相关的整数阶及时间分数阶Klein-Gordon方程进行了研究,并得到了丰富的精确行波解.这些研究采用的主要方法有椭圆方程辅助方法[4-5]、修正简单方程法[6]、首次积分法[7]、G′/G展开法[8]、同伦摄动方法[9]、Jacobi谱配置方法[10]、平面动力系统分支理论方法[11]等.但目前大部分学者研究的多为时间分数阶Klein-Gordon方程[7-11],而对于时间-空间分数阶Klein-Gordon方程研究得较少:郭琳等利用修正的黎曼-刘维尔导数及其性质以及一般椭圆方程(作为辅助方程)给出了方程(1)的部分精确解[5];M.Kaplan等利用一种修正的简单方程法求得了方程(1)的诸多行波解[6].本文针对文献[5]缺少图形支撑和文献[6]存在解法较为繁琐的问题,利用保形分数阶导数的性质和1/G展开法[12-13]对方程(1)进行求解,得到了较为丰富的孤立波解和扭曲波解.

1 1/G展开法求解分数阶方程的应用

1.1 预备知识

求解分数阶方程的方法通常是将其化为整数阶方程后再求解.由于传统的Riemann-Liouville分数阶导数定义[5]和Caputo[9]分数阶导数定义均带有积分形式,而保形分数阶导数的定义不带有积分形式(应用更为方便),因此本文采用保形分数阶导数将方程(1)变换为整数阶微分方程后再进行求解.保形分数阶导数的定义[11]为:

(2)

其中f:(0,∞)→R,t>0.

当α= 1时,保形分数阶导数为一阶导数.一般情况下,当0<α≤1且f(t)为含变量t的单项式分数阶函数时,保形分数阶导数的表达式为:

(3)

(4)

利用中值定理可证明式(4)成立,即:

1.2 G′/G展开法及其求解步骤

G′/G展开法[14]是一种借助辅助函数求解方程孤立波解的方法,其不仅具有求解步骤清晰的优点,而且得到的解的种类和数量较多.为了进一步提高G′/G展开法的应用,近年来一些学者对其进行了改进,如提出了修正的G′/G展开法[15]、扩展的G′/G展开法[16]和1/G展开法[12-13]等.由于1/G展开法在求解非线性偏微分方程时具有求解步骤简洁以及求解效果相对更好的优点,因此本文采用该方法来求解时间-空间分数阶Klein-Gordon方程(1)的解.

考虑如下具有变量x=(x1,x2,…,xl,t)的非线性分数阶偏微分方程:

(5)

(6)

其中m1,m2,…,ml∈R为任意常数,c为波速.根据式(6)可将式(5)变换为如下常微分方程:

F1(φ,φ′ξ,φ″ξξ,…)= 0,

(7)

其中φ′ξ、φ″ξξ等分别表示对共同变量ξ的求导.设方程(7)的解为1/G(ξ)的有限次幂级数,即:

(8)

其中:系数ai(i= 0,1,2,…,n)为待定常数,且an≠0,正整数n由平衡式(7)中含最高阶偏导数的项和具支配地位的非线性项的次数来确定;G(ξ)由方程(9)来确定.

G′(ξ)+λG(ξ)+1= 0,

(9)

其中λ是常数(λ≠0).

将式(8)代入式(7)后利用式(9)将式子左边化为1/G(ξ)的多项式形式,再通过合并[1/G(ξ)]i的同类项(i= 1,2,…,n)和令1/G(ξ)的各次幂项的系数为0即可得a0,a1,a2,…,an,c,λ的代数方程组.解该代数方程组后,将其结果代入式(8)中即可得到用1/G(ξ)表示的方程(5)行波解的一般形式.

2 方程(1)的孤立波解

(10)

通过平衡式(10)中的最高阶导数项φ″ξξ和最高阶非线性项φ2的次数可知,式(8)中的n= 2.由此可知方程(10)的解等价于方程(1)的解,即:

(11)

于是再由式(9)可得:

(12)

(13)

(14)

(15)

(16)

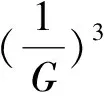
(17)

(18)

由于a2≠0,λ≠0,因此通过求解由式(14)—(18)联立的方程组可得如下几组解:

(19)

(20)

(21)

(22)

其中:解(19)、(20)需d与c2-m2为同号且都不为0,解(21)、(22)需d与c2-m2为异号且都不为0.

将解(19)代入式(11)后再结合式(9)可得方程(1)的解为:

(23)

(24)

由于双曲正切、双曲余切函数是奇函数,因此将解(20)代入式(11)后再结合式(9)可得到与式(23)、(24)分别相同的方程(1)的2个解.将解(21)代入式(11)后再结合式(9)可得到方程(1)的如下2个解:

(25)

(26)

类似于上述方法,将解(22)代入式(11)后再结合式(9)可得到方程(1)的如下2个解:

(27)

(28)

注1在解(23)、(24)中,x、t是变量,参数d、e、c、m为非0的任意常数,d与c2-m2为同号;在解(25)—(28)中,参数d、e、c、m为非0的任意常数,d与c2-m2为异号;0<α≤1.

3 解的相图分析

由上述求解方程(1)的过程可知,本文利用1/G展开法得到了8个孤立波解.但由于双曲正切、双曲余切函数是奇函数,因此使得其中的2个解(通过奇偶变换后所得的解)与式(23)、(24)所表示的解相同,所以在结果中只显示了6个解.将本文所得的解与文献[5-11]中的解进行对比可知,其结果是不同的.为了验证本文所得解的有效性,本文给出了解的相图.由于解(23)、(25)的图形类似于解(27)的图形,解(24)、(26)的图形类似于解(28)的图形,因此本文在此仅给出解(27)和(28)的图形(见图1和图2).

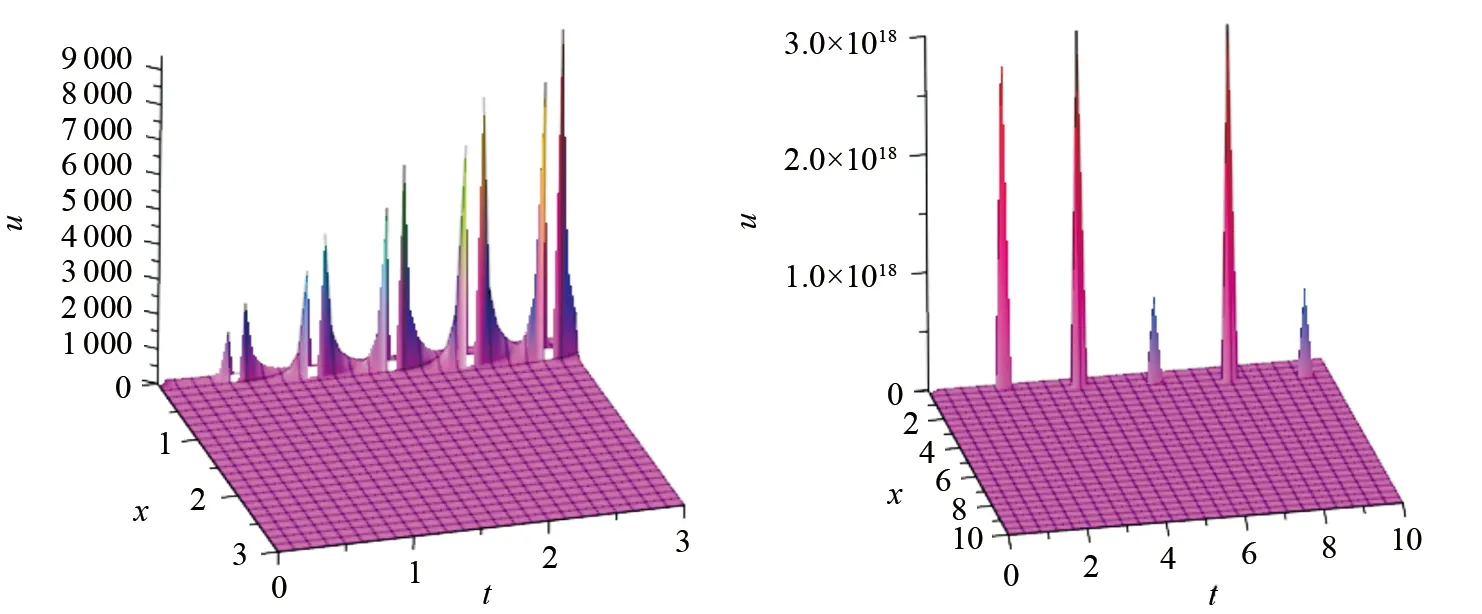
(a) x∈(-3,3), t∈(0,3) (b) x∈(-10,10), t∈(0,10)图1 参数d=8、e=4、c= 1、m=3、α= 1/2时解(27)在不同区间下的三维图像

(a) x∈(0,3), t∈(0,3) (b) x∈(0,30), t∈(0,30)图2 参数d=8、e=4、c= 1、m=3、α= 1/2时解(28)在不同区间下的三维图像

由图1(孤立波图)可以看出,图中的“孤立子”数量随变量区间的增大而减少,其原因是当区间变大时许多小的“孤立子”在高大的“孤立子”的衬托下不易显现(但当区间缩小和图形放大时,“孤立子”会明显显现).由图2(扭曲波图)可以看出,扭曲波并未随变量区间的增大而发生明显的变化(除图形“变陡”外),其原因是扭曲波在传播时具有较好的稳定性.

4 结论

本文利用1/G展开法和保形分数阶导数的定义对一类时间-空间分数阶Klein-Gordon方程进行了求解,并得到了该方程的一些精确行波解(包含孤立波解和扭曲波解).利用Maple软件对部分解的不同大小区间的三维图进行分析及数值模拟表明,所求得的这些解都是有效的.本文研究表明,1/G展开法是一种较为有效的求解非线性偏微分方程的方法,它可以求得方程的孤立波解和扭曲波解等行波解.