一类具有隔离项的时滞分数阶SIQ传染病模型的稳定性分析

王娜

( 山西工商学院 计算机信息工程学院, 太原 030006 )

0 引言

很多传染病(如霍乱、伤寒、流感、肺结核、艾滋病、鼠疫等)会严重危害人类的健康,因此做好预防工作具有重要意义.目前,已有许多国内外学者利用分数阶微积分建立了传染病模型,并对模型的稳定性和分岔等动力学特性进行了研究.例如:Mousa Mohamed等[1]建立了一个关于儿童疾病(麻疹、腮腺炎、水痘等)的分数阶“易感-感染-恢复”SIR模型,并定性考察了该模型的动力特性.Karaji等[2]建立了一个分数阶乙型肝炎流行模型,并利用分数阶Barbalat引理研究了该模型的全局动力学.Miao等[3]在分数阶SIRS传染病模型中引入了两种不同的耦合控制器,并利用不动点定理研究了Julia集的复杂性和不规则性.Wang等[4]提出了一类带有饱和方程的时滞分数阶SIR传染病模型,并在任意时滞下分析了模型的稳定性与分支情况.在上述研究的基础上,为了进一步探讨引入时滞对分数阶传染病模型的动力学特性的影响,本文建立了一类具有隔离项的时滞分数阶SIQ传染病模型,并研究了其动力学性质.

1 预备知识

定义1[5]连续函数f:(0,+∞)→R的α(α>0)阶Caputo分数阶导数为:

引理1[6]Caputo分数阶导数的Laplace变换为:

引理2[7]已知时滞分数阶系统:

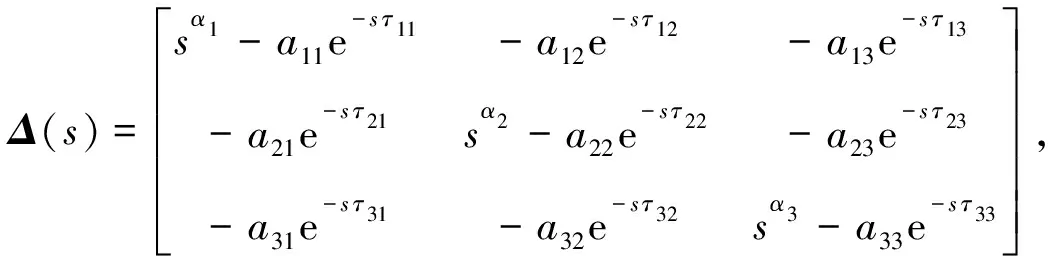
引理3[8](Routh-Hurwitz判据)已知一元多项式方程λn+a1λn-1+a2λn-2+…+an-1λ+an= 0,其所有的根均具有负实部的充要条件是:

2 具有隔离项的时滞分数阶SIQ传染病模型的建立

文献[9]的作者建立了如下一类具有隔离项的常微分SIQS的传染病数学模型:

(1)

其中:S(t)、I(t)、Q(t)分别为t时刻人群中的易感染者、感染者、隔离者人数;N(t)为t时刻人群总人数,N(t)=S(t)+I(t)+Q(t);A为感染者人群对易感人群的感染率;β为易感人群与感染者的有效接触率;d、η1、η2分别为人群的自然死亡率、染病人群的死亡率、隔离人群的死亡率;δ为染病人群的隔离率;r为染病人群的恢复率;ε为隔离人群的恢复率.

本文建立如下一类具有隔离项的时滞分数阶SIQ传染病模型:

(2)

(3)

将系统(3)进行Laplace变换可得:

(4)

式(4)中L[S(t)]、L[I(t)]、L[Q(t)]分别为S(t)、I(t)、Q(t)的Laplace变换.对式(4)进行化简可得:

(5)

其中:Δ(s)为系统(2)的特征矩阵,det(Δ(s))= 0为系统(2)的特征方程.另外,式(5)中的Δ(s)、v1(s)、v2(s)、v3(s)分别可表示为:

v3(s)=sα3Q(0).

3 解的稳定性及其Hopf分岔行为

3.1 系统(2)的平衡点及其基本再生数的计算

(6)

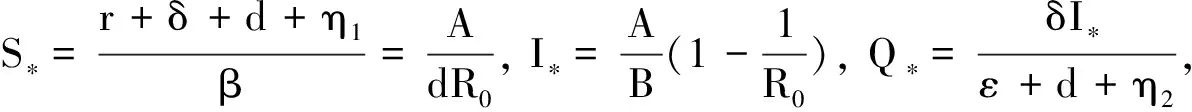
3.2 主要结论及其证明

3.2.1系统(2)在无病平衡点E0处的稳定性

定理1对于所有τ≥0,当R0<1时,系统(2)在无病平衡点E0处为局部渐近稳定;当R0>1时,系统在无病平衡点E0处为不稳定.

(7)

下面分τ= 0和τ>0两种情况讨论系统(2)在无病平衡点处的稳定性.

(i)当τ= 0时,设λi=sαi,i= 1,2,3,则式(7)可化简为:

(8)

(ii)当τ>0时,式(7)可化简为:

(9)

设λi=sαi,i= 1,3,则式(9)的2个特征值分别为λ1=-d<0,λ3=-(ε+d+η2)<0.由于式(9)的左边第2个因子包含时滞τ,故应考虑如下方程的根:

(10)

令s= iω(ω>0),并将其代入式(10)中可得:

(11)

分离式(11)中的实部和虚部可得:

(12)

将式(12)中的2个方程分别进行平方、求和并化简后可得:

(13)

当R0<1时,由根与系数的关系可知方程(13)没有正实根.由此可知,式(9)的特征值实部均为负.于是再由引理2可知,系统(2)在无病平衡点E0处是局部渐近稳定的.当R0>1时,由根与系数的关系可知方程(13)有正实根,系统(2)在无病平衡点E0处的特征值不满足Re[s]<0,故由引理2可知系统(2)在无病平衡点E0处是不稳定的.

3.2.2系统(2)在地方病平衡点E*处的稳定性

系统(2)在地方病平衡点E*=(S*,I*,Q*)处的特征方程为:

(14)

整理式(14)可得:

f1(s)+f2(s)e-sτ= 0.

(15)

其中:f1(s)=sα1+α2+α3+a1sα1+α2+a2sα1+α3+a3sα2+α3+a4sα1+a5sα2+a6sα3+a7,f2(s)=- (b1sα1+α3+b2sα3+b3sα1+b4),a1= (ε+d+η2),a2=r+δ+d+η1,a3=βI*+d,a4= (ε+d+η2)(r+δ+d+η1),a5= (βI*+d)(ε+d+η2),a6= (βI*+d)(r+δ+d+η1),a7= (βI*+d)(ε+d+η2)(r+δ+d+η1),b1=βS*,b2=βrI*+βdS*,b3=βS*(ε+d+η2),b4=(βrI*+βdS*)(ε+d+η2).

由注1可知,当R0>1时,地方病平衡点(E*=(S*,I*,Q*))中的S*>0,I*>0;因此,ai(i= 1,2,3,4,5,6,7)和bj(j= 1,2,3,4)均为正数.

定理2假设系统(2)的分数阶α1=α2=α3=α∈(0,1].当时滞τ= 0,R0>1,a1+a2+a3-b1>0, (a1+a2+a3-b1)(a4+a5+a6-b2-b3)-(a7-b4)>0时,系统(2)在地方病平衡点E*处是局部渐近稳定的.

证明当时滞τ= 0时,化简式(15)可得f1(s)+f2(s)= 0,即:

sα1+α2+α3+a1sα1+α2+a2sα1+α3+a3sα2+α3+a4sα1+a5sα2+a6sα3+a7-

b1sα1+α3-b2sα3-b3sα1-b4= 0.

(16)

由于α1=α2=α3=α∈(0,1],因此方程(16)可简化为:

s3α+(a1+a2+a3-b1)s2α+(a4+a5+a6-b2-b3)sα+a7-b4= 0.

(17)

令sα=λ,于是方程(17)可简化为:λ3+p1λ2+p2λ+p3= 0,其中p1=a1+a2+a3-b1,p2=a4+a5+a6-b2-b3,p3=a7-b4.根据定理2中的已知条件可得:

H1=p1=a1+a2+a3-b1>0,

H2=p1p2-p3=(a1+a2+a3-b1)(a4+a5+a6-b2-b3)-(a7-b4)>0.

再由引理3中的Routh-Hurwitz判据知,系统(2)在地方病平衡点E*处的特征方程的根均具有负实部.因此由引理2知,当时滞τ= 0且系统(2)的分数阶α1=α2=α3=α∈(0,1]时,系统(2)在地方病平衡点E*处是局部渐近稳定的.

3.2.3系统(2)在地方病平衡点E*处的Hopf分岔行为

1)当τ<τ0时,系统(2)在地方病平衡点E*处是局部渐近稳定的;

2)当τ>τ0时,系统(2)在地方病平衡点E*处是不稳定的.

证明当时滞τ>0,且系统(2)的分数阶α1=α2=α3=α∈(0,1]时,式(15)可化简为:

s3α+(a1+a2+a3)s2α+(a4+a5+a6)sα+a7-[b1s2α+(b2+b3)sα+b4]e-sτ= 0.

(18)

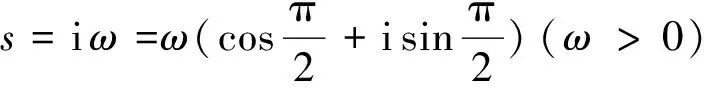
T1+iT2-[cos(ωτ)-isin(ωτ)](T3+iT4)= 0,

(19)

其中:

(20)

(21)

(22)

(23)

分离方程(19)的实部和虚部可得:

(24)

再由式(20)可得:

(25)

于是由cos2(τω)+ sin2(τω)= 1可得关于ω的方程:

(26)

4 结论

本文建立了一类具有隔离项的时滞分数阶SIQ传染病模型,并利用分数阶系统稳定性的相关理论研究了当时滞τ≥0时,系统(2)在无病平衡点E0处的稳定情况,同时给出了其局部渐进稳定的充分条件.以时滞为参数,利用Hopf分岔理论对系统(2)在地方病平衡点E*处所发生的Hopf分岔行为进行计算并分析表明:当τ<τ0(临界阈值)时,系统(2)在地方病平衡点E*处是局部渐近稳定的;当τ>τ0时,系统(2)在地方病平衡点E*处是不稳定的.本文结果可为研究具有隔离项的时滞分数阶传染病系统的动力学特性提供参考.