扩展的Jacobi椭圆函数展开法在求解Chen-Lee-Liu方程精确解中的应用
赵雁楠
( 山西工商学院 计算机信息工程学院, 太原 030000 )
0 引言
由于非线性发展方程可用来描述自然界的许多复杂现象,因此近年来许多学者对求解其精确解进行了研究.目前,求解非线性发展方程精确解的方法主要有齐次平衡法[1]、双曲函数法[2]、反散射方法[3]、sine-cosine方法[4]、Backlund方法[5]、Darboux变换法[6]、Jacobi椭圆函数展开法和扩展的Jacobi椭圆函数展开法[7-11]等.
Chen-Lee-Liu(CLL)方程(方程(1))又被称作DNLSE-Ⅱ方程,它可用于描述光脉冲在介质中的传播现象.近年来,许多学者对CLL方程进行了求解.例如:文献[12]的作者通过F展开法得到了方程(1)的包络孤立波解和包络正弦波解;文献[13]的作者通过扩展的tanh展开法得到了方程(1)的多种光孤子解,如暗孤子解、奇异孤子解、暗奇异孤子解、奇异周期波解等;文献[14]的作者利用奇数阶Darboux变换法得到了方程(1)的精确周期波解和怪波解;文献[15]的作者利用Jacobi椭圆函数展开法获得了方程(1)的一些新的孤立波解;文献[16]的作者利用扩展的直接代数法得到了方程(1)的一些新解,如暗、亮、组合暗-亮、组合亮奇异和周期奇异孤子解等.为了获得更多的CLL方程的精确解,本文将利用扩展的Jacobi椭圆函数展开法研究CLL方程的精确解.
iqt+αqxx+iβqq*qx= 0.
(1)
其中:q(x,t)为光孤子的分布函数,q*为q(x,t)的共轭函数,α为群速度的色散系数,β为非线性系数,且α和β均为实常数.
1 扩展的Jacobi椭圆函数展开法
扩展的Jacobi椭圆函数展开法的一般计算步骤为:
第1步 将非线性偏微分方程转化为非线性常微分方程,即将PDE化为ODE.考虑如下非线性偏微分方程PDE:
F(φ,φ2,φx,φt,φxx,…)= 0.
(2)
为构造方程(2)的Jacobi椭圆函数解的形式,本文引入如下变换:
φ(x,t)=Φ(ξ),ξ=ax-ct.
(3)
将式(3)代入方程(2)可得非线性常微分方程ODE为:
L(Φ(ξ),Φ2(ξ),Φ′(ξ),Φ″(ξ),…)= 0,
(4)
其中a和c为实常数.
第2步 设定解的形式.假设方程(4)的解可展开为Jacobi椭圆函数的有限级,即:
(5)
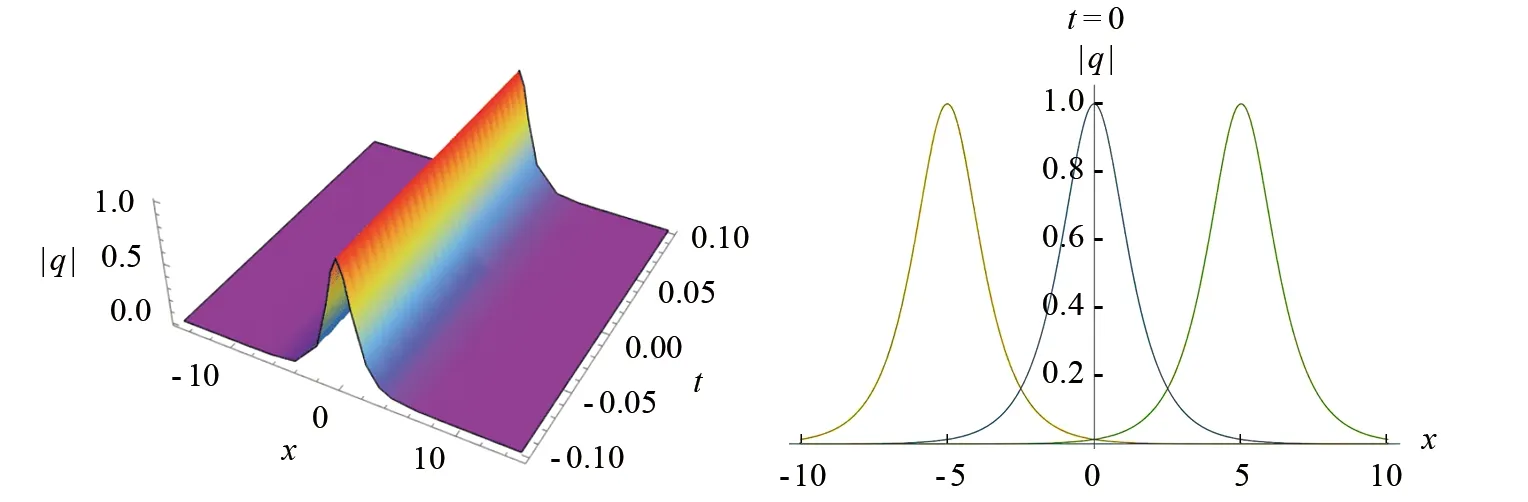
其中:Y(ξ)有3种情况,分别为Y(ξ)=sn(ξ,m),Y(ξ)=cn(ξ,m),Y(ξ)=dn(ξ,m)(0 第3步 确定M值.利用方程(4)中非线性项的最高阶数和导数项的最高阶数来求得M值.非线性项和导数项的最高阶数为: (6) 第4步 求解待定系数bj(j=-M,…,M).将式(5)代入方程(4)可得关于Jacobi椭圆函数Y(ξ)的方程.化简该方程后令Y(ξ)的各次幂系数为零可得到一个关于bj(j=-M,…,M)的方程组,由此再借助Mathematica软件求解该方程组即可求得bj(j=-M,…,M)值. 第5步 确定方程(1)的周期解.将在第4步中求得的bj(j=-M,…,M)代入式(5)即可求得方程(1)的新周期解. 注记1为了便于应用扩展的Jacobi椭圆函数展开法,本文给出如下3种关系式[17]: 1)恒等形式:sn2(ξ,m)+cn2(ξ,m)= 1,dn2(ξ,m)+m2sn2(ξ,m)= 1,m2cn2(ξ,m)+1-m2=dn2(ξ,m),cn2(ξ,m)+(1-m2)sn2(ξ,m)=dn2(ξ,m). 2)导数形式:sn′(ξ,m)=cn(ξ,m)dn(ξ,m),cn′(ξ,m)=-sn(ξ,m)dn(ξ,m),dn′(ξ,m)=-m2sn(ξ,m)cn(ξ,m). 3)极限形式:m→1,sn(ξ,m)→tanhξ,cn(ξ,m)→sechξ,dn(ξ,m)→sechξ;m→0,sn(ξ,m)→sinξ,cn(ξ,m)→cosξ,dn(ξ,m)→1. 假定方程(1)解的形式为: q(x,t)=Q(ξ)eiφ,ξ=μ(x-ct),φ=ax-wt, (7) 其中μ、c、a、w为实常数.将式(7)代入方程(1)可得: 由上式可得ODE的实数和虚数部分分别为: αμ2Q″+(w-αa2)Q-βaQ3= 0, (8) (c-2αa-βQ2)μQ′= 0, (9) 其中“′”表示Q对ξ的导数. 根据齐次平衡法[17]平衡式(8)中的Q″和Q3可得Jacobi椭圆函数的有限级数M= 1,于是方程(1)的解可设为: Q(ξ)=b-1Y-1(ξ)+b0+b1Y(ξ). (10) 将式(10)代入方程(8)可得关于Jacobi椭圆函数Y(ξ)的方程,再利用注记1化简该方程后令Y(ξ)的各次幂系数为零可得到一个关于bj(j=-1,0,1)的方程组,由此再借助Mathematica软件求解该方程组即可求得bj(j=-1,0,1)值. 情形1 当取Y(ξ)=sn(ξ,m)时,借助Mathematica软件可得到式(7)、(10)中b-1、b0、b1、w的值: exp[i(ax-α(a2+μ2+6mμ2+m2μ2)t)]. (11) exp[i(ax-α(a2+μ2-6mμ2+m2μ2)t)]. (12) (13) (14) 情形2 当取Y(ξ)=cn(ξ,m)时,借助Mathematica软件可得到式(7)、(10)中b-1、b0、b1、w的值: (15) (16) (18) 情形3 当取Y(ξ)=dn(ξ,m)时,借助Mathematica软件可得到式(7)、(10)中b-1、b0、b1、w的值: (19) (20) (22) 1)当m→1时,由Jacobi椭圆函数的定义可知sn(ξ,m)→tanhξ,cn(ξ,m)→sechξ,dn(ξ,m)→sechξ,且有如下情形: 情形1 当sn(ξ,m)→tanhξ时,方程(11)、(12)、(13)、(14)可化简为如下形式: exp[i(ax-α(a2+8μ2)t)]. (23) exp[i(ax-α(a2-4μ2)t)]. (24) (25) (26) 情形2 当cn(ξ,m)→sechξ时,方程(15)、(16)、(18)可化简为如下形式: (27) 情形3 当dn(ξ,m)→sechξ时,方程(19)、(20)、(22)可化简为如下形式: (28) 2)当m→0时,由Jacobi椭圆函数的定义可知sn(ξ,m)→sinξ,cn(ξ,m)→cosξ,且有如下情形: 情形1 当sn(ξ,m)→sinξ时,方程(11)、(12)、(13)可化简为如下形式: (29) 情形2 当cn(ξ,m)→cosξ时,方程(15)、(16)、(17)可化简为如下形式: (30) 为了更加直观地描述CLL方程的孤波解,本文通过选取特定的参数给出了CLL方程解(26)、(27)、(29)、(30)的孤波图,如图1—图4所示.从图1和图2中的3D图可以看出,当取相同的参数和退化形式(α= 2,β= 2,a= 2,c= 0.1,μ= 1),而Y(ξ)取不同的函数时,CLL方程的孤波方向发生了改变;从图2和图3中的3D图可以看出,当取相同的参数(α= 2,β= 2,a= 2,c= 0.1,μ= 1),而取不同的退化形式和Y(ξ)函数时,CLL方程的孤波形状发生了显著变化.从图1—图4中的2D图可以看出,孤立波的振幅不随时间的变化而发生变化,但其空间位置发生了变化.这表明光孤子在传播中不随时间而改变其形状、大小和方向,即其具有很好的稳定性. 图1 式(26)的3D和2D孤波图(α=2,β=2,a=2,c=0.1,μ=1,m=1) 图2 式(27)的3D和2D孤波图(α=2,β=2,a=2,c=0.1,μ=1,m=1) 图3 式(29)的3D和2D孤波图(α=2,β=2,a=2,c=0.1,μ=1,m=0) 图4 式(30)的3D和2D孤波图(α=2,β=1,a=4,c=0.6,μ=0.01,m=0)
2 扩展的Jacobi椭圆函数展开法在CLL方程中的应用
2.1 CLL方程的周期波解
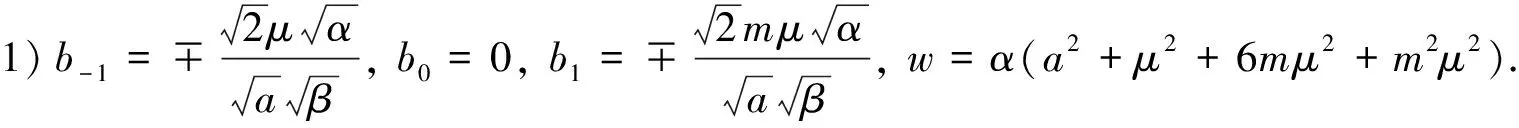


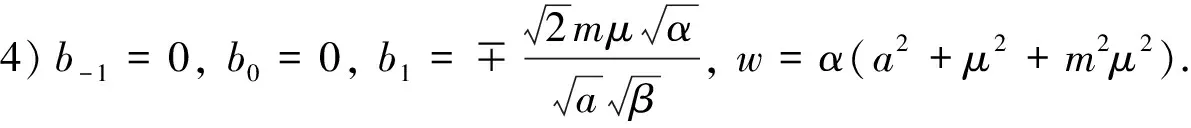

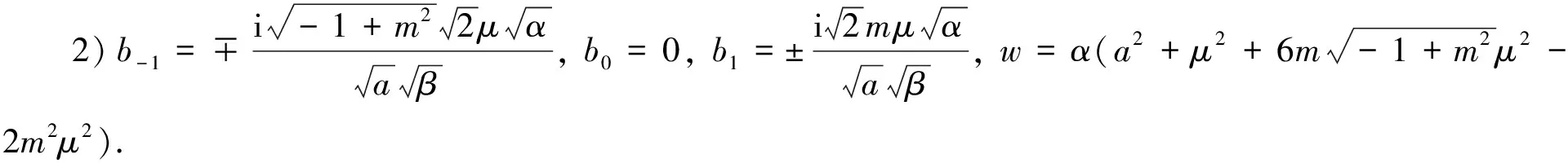






2.2 周期波解的退化形式