无界区域上一类带有权函数的半线性椭圆方程解的存在性
2023-05-17 05:18韩亮谢君辉
延边大学学报(自然科学版) 2023年1期
韩亮, 谢君辉
( 湖北民族大学 数学与统计学院, 湖北 恩施 445000 )
0 引言
本文研究如下无界区域上的一类带有权函数的半线性椭圆方程:
(1)

当问题(1)中的Ω不包含原点时,问题(1)是带权函数的半线性椭圆方程.文献[11]的作者用变分原理和山路引理讨论了如下无界区域上的半线性椭圆方程解的存在性:
(2)

(3)
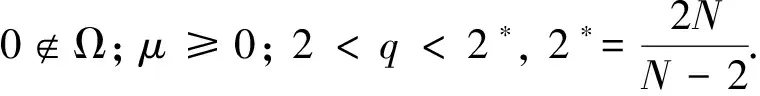
当问题(1)中的Ω为包含原点的区域时(系数有奇性),称问题(1)是带有Hardy项的半线性椭圆方程的边值问题.文献[13]的作者研究了如下无界区域上的一类带Hardy项且具有临界指数的半线性椭圆方程非平凡解的存在性:
(4)
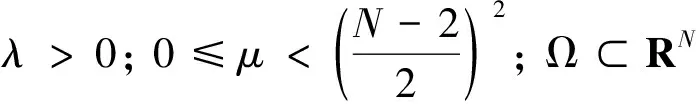
(5)
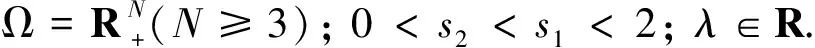
1 预备知识
对任意的u∈H(Ω),问题(1)所对应的能量泛函为:
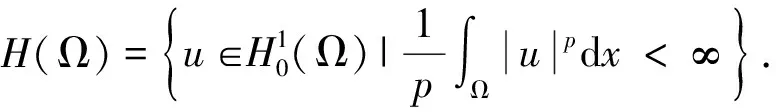

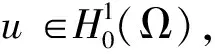
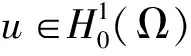


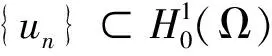
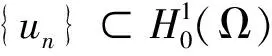
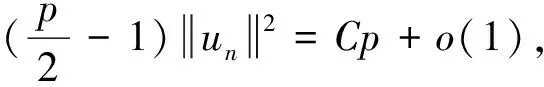

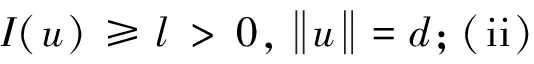
引理5[16](偶泛函临界点定理)设E是一个无限维的Banach空间,偶泛函I∈C1(E,R)满足PS条件和以下条件:
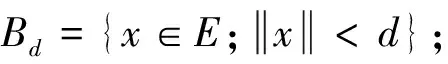
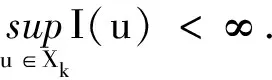
Γm={K⊂E;K关于0是紧对称的且∀h∈Γ1,ψ(K∩h(∂B1))≥m}.

1)当0 2)若对某个m∈{1,2,…,k}有bm=bm+1成立,则对于每个bm,泛函I有无穷多个临界点.2 主要结果及其证明
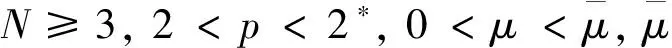

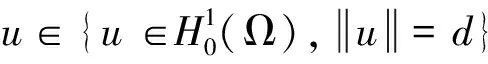

猜你喜欢
科学技术创新(2022年33期)2022-11-12
海洋通报(2022年4期)2022-10-10
数学物理学报(2022年5期)2022-10-09
数学物理学报(2021年4期)2021-08-30
传感器与微系统(2019年8期)2019-08-15
数学物理学报(2018年1期)2018-03-26
政工学刊(2017年2期)2017-02-20
中央民族大学学报(自然科学版)(2015年3期)2015-06-11
中北大学学报(自然科学版)(2015年3期)2015-03-11
数学物理学报(2014年3期)2014-03-11

