基于PCA-GRNN模型的新能源汽车月度销售量预测研究

谢萍萍

( 黎明职业大学 智能制造工程学院, 福建 泉州 362000 )

0 引言

近年来随着石油能源危机和生态环境压力的进一步加大,新能源汽车已逐步代替传统汽车,并呈快速发展趋势,如2019年我国新能源车的销售量为120.6万辆,2020年为136.7万辆,2021年为352.1万辆.目前,预测销售量通常采用时间序列模型[1]、回归分析模型[2]、灰色模型[3]等方法,但时间序列模型和回归分析模型对解决多元非线性问题具有局限性,而灰色神经网络则存在易陷入局部极小和收敛速度慢等问题.研究显示,组合模型可以更好地挖掘数据的内部特征,提高预测的精度.例如:O.Kitapc等[4]利用多元回归和神经网络分析法对土耳其的汽车销售量进行了预测;周彦福等[5]利用果蝇算法优化灰色神经网络模型后对新能源汽车的月度销售量进行了预测.广义回归神经网络(general regression neural network,GRNN)是一种建立在数理统计基础上的径向基函数网络,由于它能够较好地解决非线性问题以及提高少量数据或者数据不稳定时的预测效果,因而受到学者们的关注[6].目前,使用GRNN预测销售量的相关研究较少.梁达强[7]和王红卫等[8]利用GRNN分别对木浆和灯具的销售量进行了预测,但其研究均将所选的影响因子直接作为预测模型的输入变量(未对影响因子进行降维),因此其计算速度和预测精度存在不足.为此,本文将主成分分析(principal component analysis,PCA)方法与GRNN方法相结合,提出了一种PCA-GRNN预测模型,并对我国新能源汽车的月度销售量进行了预测.

1 相关理论介绍

1.1 主成分分析

PCA是一种多变量统计分析方法,该方法将原来的多个变量化为少数几个主成分,以此实现降维并用以特征提取和数据压缩.PCA的基本模型为:

(1)

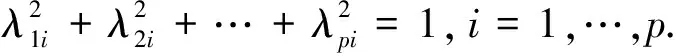
1.2 广义回归神经网络

图1 广义回归神经网络结构

1.3 误差分析方法

2 数据建模及其分析

2.1 影响因子指标的选取

影响新能源汽车月度销售量的因素较多,本文根据文献[11-13]的研究结果选取动力电池月份装车量X1(GW·h)、充电基础设施X2(万台)、电池级碳酸锂平均价格X3(万元/t)、交通和通信类居民消费价格指数X4(上年同月=100)、全国城镇调查失业率X5(%)、汽车制造业工业生产者出厂价格指数X6(上年同月=100)等6个影响因子作为构建新能源汽车月度销售量Y(万辆)预测模型的因子指标,各年份及其月份的数据见表1.表1中的数据来源于国家统计局、中国汽车工业协会以及网络公开资料.

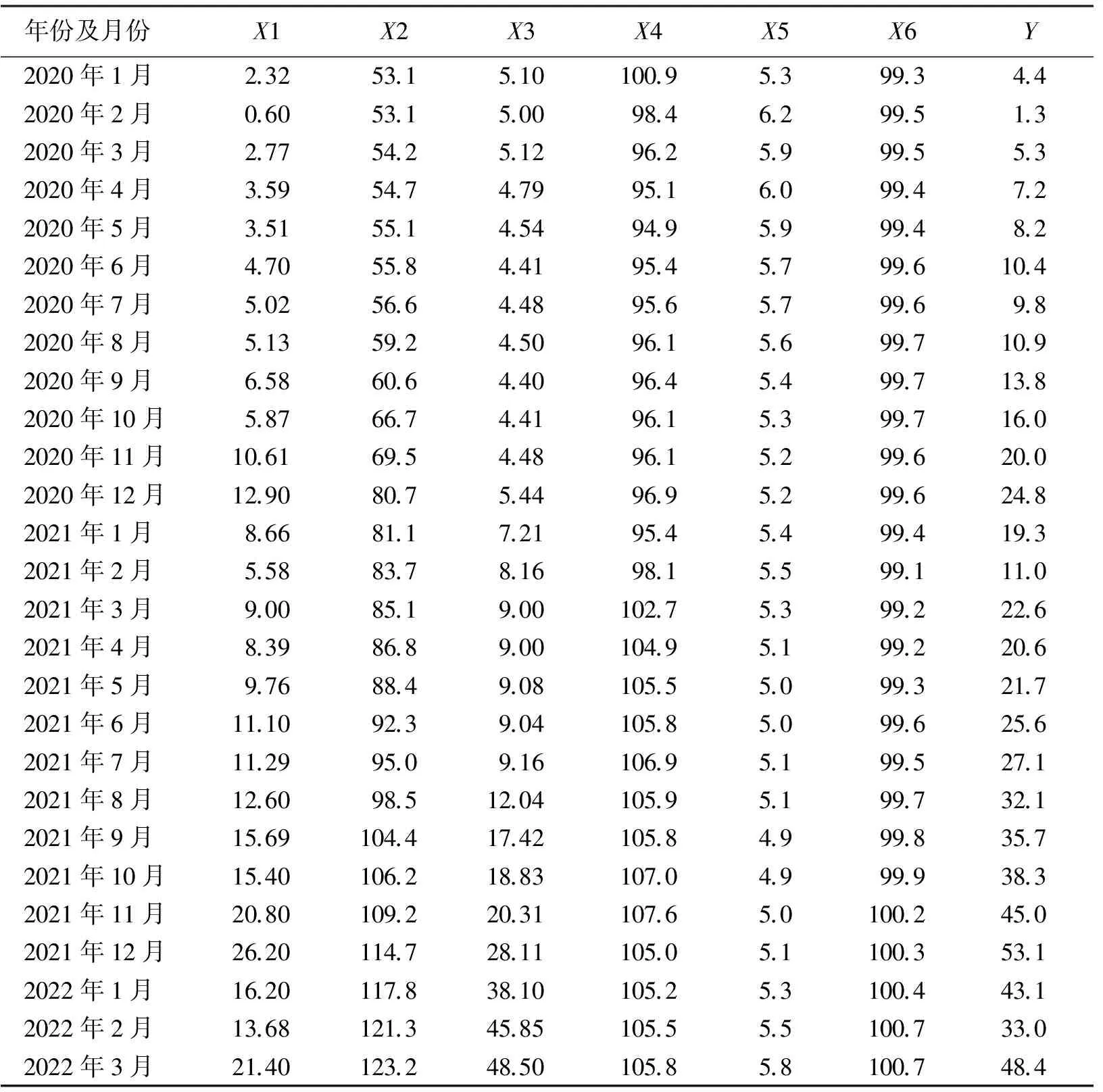
表1 影响新能源汽车月度销售量的因子指标及其数值

2.2 影响因子的主成分分析

采用SPSS软件对因子指标进行主成分分析,其分析主要包括:因子相关系数矩阵、KMO和Bartlett’s球形检验、因子总方差的解释.

1)因子相关系数矩阵.表2为新能源汽车销售量影响因子的相关性矩阵.由表中的相关系数可知,各个影响因子之间的相关性较强,因此需利用主成分分析法对其进行降维来消除各影响因子间的相关性,以减少预测模型的输入变量.

表2 因子的相关性矩阵

2) KMO和Bartlett’s球形检验.经检验,KMO检验的结果为0.685,这表明所选因子适用于主成分分析;Bartlett’s球形检验的显著性结果为p=0 (小于0.001),该结果进一步表明所选因子适用于主成分分析.

3)因子总方差的解释.表3为新能源汽车销售量影响因子的总方差解释表.由表3可知,成分1和成分2的方差解释率累计为89.625%(成分1的方差解释率为71.615%,成分2的方差解释率为18.011%),表明这两个成分包含了6个影响因子的大部分信息,可以作为主成分分析的条件.

表3 因子总方差的解释

2.3 PCA-GRNN模型的建立与预测分析

2.3.1PCA-GRNN模型的建立

建模时首先根据表1中的影响因子数据在SPSS软件中计算出主成分1和主成分2,然后在Matlab软件中调用Matlab神经网络工具箱中的GRNN神经网络函数建立GRNN神经网络预测模型.按上述建立的预测模型如图2所示.

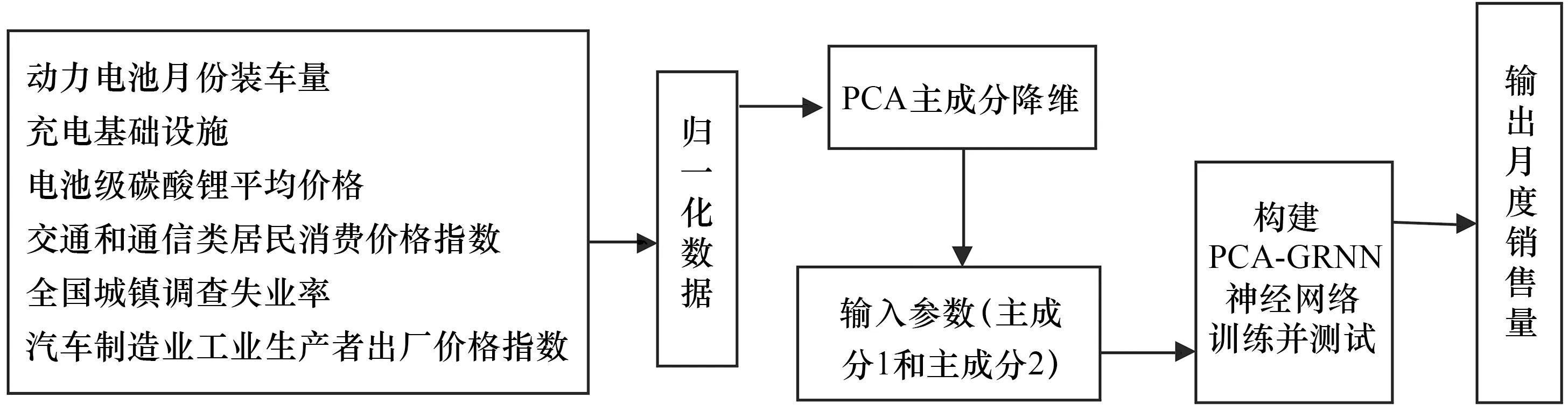
图2 PCA-GRNN模型的结构

2.3.2预测方法与结果分析

预测时,将表1中的2020—2021年的24个月度数据作为模型训练数据,并将其随机分为24组;在每个组内,将前23个月度数据作为训练样本,将最后的1个月的月度数据作为测试样本.计算时,模型的分布密度值取0.1～1.0(采用试验法获得)[14].

为检验PCA-GRNN模型的有效性,将PCA-GRNN模型与PCA-BP、PCA-Elman模型进行了对比.PCA-BP模型和PCA-Elman模型是通过调用Matlab软件中的BP和Elman神经网络函数建立的,其中输入层为主成分1和主成分2,输出层为月度销售量,隐含层的节点数为2.PCA-BP模型中的隐含层的激活函数分别为tansig函数和purelin函数,输出层函数为trainlm函数;PCA-Elman模型中的隐含层的激活函数分别为tansig函数和purelin函数,输出层函数为traingdm函数.3个模型均采用相同的月度数据进行学习训练.3个模型完成训练后,以2022年1—3月的样本数据对其进行预测和性能对比.图3为3个模型的预测结果.由图可以看出,3个模型预测的销量趋势基本一致,即总体呈现稳步增长趋势.

图3 3种模型预测新能源汽车月度销售量的预测值与实际值的对比

图4为3种模型预测的新能源汽车月度销售量的相对误差 (预测数据的月份为2020年1月—2021年12月).由图4可见,3个模型预测的相对误差除2020年2月和2021年12月超过10%外,其余月份均在10%以内.2020年2月出现预测值相对误差较大的主要原因是销售受到了新冠疫情的影响(销售量仅达到1.3万辆);2021年12月出现预测值相对误差较大的主要原因是销售受到了新能源汽车财政补贴政策调整预期的影响(销售量达到53.1万辆).经计算,PCA-GRNN、PCA-BP和PCA-Elman模型预测的新能源汽车月度销售量的平均相对误差分别为5.34%、6.78%和6.42%.该结果表明,PCA-GRNN模型的预测效果优于PCA-BP和PCA-Elman模型.

表4为3种模型对2022年1—3月的新能源汽车月度销售量的预测结果.由表4可知,PCA-GRNN、PCA-BP和PCA-Elman模型预测的平均相对误差分别为4.00%、4.77%和4.29%,该结果进一步表明PCA-GRNN模型的预测效果优于PCA-BP和PCA-Elman模型.

图4 3种模型预测新能源汽车月度销售量的相对误差

表4 3种模型对2022年1—3月新能源汽车销售量的预测结果

3 结论

利用本文提出的PCA-GRNN模型对2022年1—3月的新能源汽车月度销售量进行预测显示,其平均相对误差为4.00%,低于PCA-BP和PCA-Elman模型预测的平均相对误差(分别为4.77%和4.29%),因此本文提出的预测模型具有一定的实用价值.由于影响销售的因素较多,因此在今后的研究中笔者将增加其他因素(如财政补贴标准和汽车芯片产能等指标)以及采用遗传算法等来进一步提高本文模型的适用性.