关联平面内四个点的一个恒等式及其空间类比

重庆市长寿龙溪中学(401249) 吴波

1 圆内接四边形中的一个恒等式

在文献[1]中我们将杨学枝老师在文献[2]中得到的关于圆内接四边形的一个恒等式变形为如下等价形式:

定理1[1]如图1,凸四边形ABCD有外接圆,P为空间中任意一点,则:|PA|2S∆BCD+|PC|2S∆ABD=|PB|2S∆ACD+|PD|2S∆ABC.

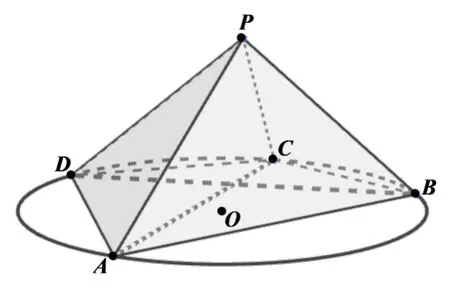
图1

文献[1]中的证明依赖于用行列式表述的四点共圆的充要条件.本文中我们给出这个行列式的几何意义,由此可以得到关联平面内四个点的一个恒等式,这个恒等式给出了定理1 的一个推广.最后我们还将此恒等式类比到空间——即得到关联空间中五个点的一个恒等式.

约定本文中提到的面积均为有向面积,体积也为有向体积,并遵从通常的符号规则.

2 预备定理

先介绍几个引理:

引理1在平面直角坐标系中,

引理2对∆ABC所在平面内任意一点O,有如下恒等式成立:S∆ABC=S∆OAB+S∆OBC+S∆OCA.

引理3在空间直角坐标系中,

引理1 至引理3 是几何中的常见结论,证略.

引理4[3]在平面直角坐标系中,∆ABC外接圆方程为:

引理5在空间直角坐标系中,四面体ABCD外接球方程为:.

简证此方程显然是表示一个球.又,由行列式性质知:此球显然经过此四面体的四个顶点.而空间不共面的四个点唯一确定一个球.因此,这个方程就是四面体ABCD外接球方程.证毕.

3 一个行列式的几何意义

先给出下面这个与圆方程有关的代数式的几何意义.

定理2若实数d,e,f满足d2+e2>f,记f(x,y)=x2+y2+2dx+2ey+f.在平面直角坐标系中,f(x,y)=0表示一个圆,将其圆心(−d,−e)记作K,半径记作r,则f(xp,yp)=|PK|2−r2,即f(xp,yp)的几何意义是点P关于⊙K的幂.

证明配方可知:

所以f(xP,yP)=(xP+d)2+(yP+e)2−r2=|PK|2−r2.证毕.

定理3在平面直角坐标系中,∆ABC外接圆半径为R,点D到∆ABC外心的距离为d,则:

即上式左侧这个行列式的几何意义是:点D关于∆ABC外接圆的幂的2S∆ABC倍.

证法一容易验证:定理3 中行列式的值对平面直角坐标系具有平移不变性.因此我们不妨设∆ABC的外心为原点O,在此坐标系下有:所以

上面最后一步用到了引理1.证毕.

证法二将定理3 中行列式与引理4 中行列式对照可知:定理3 中行列式是将点D的坐标(xD,yD)代入引理4 中∆ABC外接圆方程中左边那个行列式所得.又,展开易知:引理4 中∆ABC外接圆方程中“x2+y2”的系数为(用到引理1).而定理2 中f(x,y)的“x2+y2”的系数为1,将其扩大2S∆ABC倍即知定理3 的结论成立.证毕.

4 关联平面内四个点的一个恒等式

由定理3 我们可以证明:

定理4如图2,平面内有四点A1,A2,A3,A4(其中任三点不共线),对1,2,3,4 的任一排列i,j,k,l,将过点Aj,Ak,Al的圆记作⊙Oi(圆心即为⊙Oi),其半径为Ri,|OiAi|=di,则

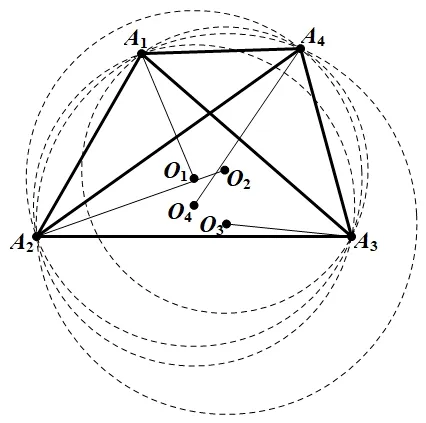
图2

证明对A1,A2,A3｜,A4应用定理3 有:

而这两个行列式的值显然互为相反数,因此

类似地,还有另两外两个也与它们相等.证毕.

由定理3 我们还可得:

定理5A1,A2,A3,A4,P是平面内五点,∆A1A2A3外接圆半径为R,A4到∆A1A2A3外心的距离为d.则.

证明以P为原点建立平面直角坐标系,设Ai(xi,yi)(i=1,2,3,4),则对A1,A2,A3,A4应用定理3 可得:

将此行列式按第一列展开并结合引理1 可知(注意有向面积中的字母有顺序):

上式两边同时改变符号即得定理5 中的结论.证毕.

说明改变定理4 中连等式的符号就可以与定理5 中等式连等起来,因此可以视为一个恒等式.

将定理5 中的A4改写为Q,并将定理5 中的恒等式移项变形,可得定理5 的如下等价形式:

推论1∆A1A2A3外接圆半径为R,点P,Q是∆A1A2A3所在平面内任意两点,Q到∆A1A2A3外心的距离为d,则.

当P,Q重合时可得文献[4]中的定理5:

推论2[4]∆A1A2A3外接圆半径为R,点P是∆A1A2A3所在平面内任意一点,P到∆A1A2A3外心的距离为d,则.

此外,当A1,A2,A3,,A4四点共圆时,d=R,由定理5 可得:

推论3平面内A1,A2,A3,,A4四点共圆,对平面内任意一点P,有.

对比推论3 与定理1,两个结论在形式上完全一致! 但推论3 的改进之处在于:利用有向面积表述之后,只要求四点共圆,对四点的顺序不作要求.但定理1 中的点P是空间中的任意点,这让我们想到:推论3,甚至于定理5 中的点P是否也可以推广为空间中的任意点呢? 经过探讨,确实如此!即有:

定理6如图3,A1,A2,A3,,A4是平面内四点,P是空间中任意点.∆A1A2A3外接圆半径为R,A4到∆A1A2A3外心的距离为d.则

证明当点P也在该平面内时,定理5 已经表明结论成立.当点P在该平面外时,如图3,设P到平面的距离为h,P在平面内的正投影为O,则

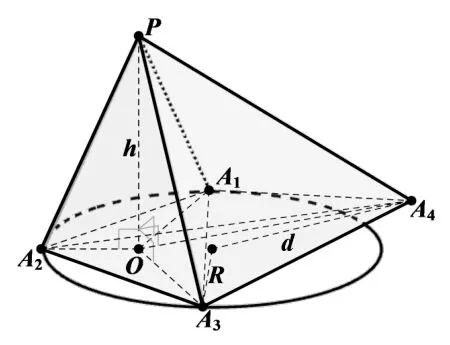
图3

|PAi|2=h2+|OAi|2(i=1,2,3,4).代入定理6 中待证恒等式的左边得:

因O在平面内,对O应用定理5 可知:上式前四项之和等于.

这正好与定理6 中待证恒等式的右边抵消! 因此只需证最后一项等于0 即可.而它显然等价于下式:如图3,当四边形A1A2A3A4是凸四边形时,很容易看出上式左右两边其实都等于四边形A1A2A3A4的有向面积,因此左右显然相等.但如果四边形A1A2A3A4是凹的或者边与边有交点的四边形,上式就不那么明显了.此时由引理2 知:

同理,定理5 推论1 推论3 的点P都可以推广到空间中的任意点,因此定理6 是定理1 的一个非常一般的推广.

5 关联空间中五个点的一个恒等式

我们看到平面内的引理1 与引理4 可分别类似于空间中的引理3 与引理5.如果定理2 定理3 在空间中的类比也成立,那么定理4 定理5 就自然可以类比到空间中.可以证明:这些类比都是成立的!

本小节中我们将这些类比结果罗列如下,而具体证明留给读者.

定理7若实数d,e,f,g满足d2+e2+f2>g,记f(x,y,z)=x2+y2+z2+2dx+2ey+2fz+g.在空间直角坐标系中,f(x,y,z)=0 表示一个球,将其球心(−d,−e,−f)记作K,半径记作r,则f(xp,yp,zp)=|PK|2−r2,即f(xp,yp,,zp)的几何意义是点P关于球K的幂.

定理8在空间直角坐标系中,四面体ABCD外接球半径为R,点E到四面体ABCD外心的距离为d,则

即上式左侧这个行列式的几何意义是:点E 关于四面体ABCD外接球的幂的6V四面体ABCD倍.

定理9空间中有五点A1,A2,A3,A4,A5(其中任四点不共面),对1,2,3,4,5 的任一排列i,j,k,l,m,将过点Aj,Ak,Al,Am的球记作球Oi(球心即为Oi),其半径为Ri,|OiAi|=di,则

定理10A1,A2,A3,A4,A5,P是空间中任意六点,四面体A1A2A3A4外接球半径为R,A5到四面体A1A2A3A4外心的距离为d.则

将定理10 中的A5改写为Q,并将定理10 中的恒等式移项变形,可得定理10 的如下等价形式:

推论1四面体A1A2A3A4外接球半径为R,点P,Q是空间中任意两点.Q到四面体A1A2A3A4外心的距离为d,则当P,Q重合时可得:

推论2四面体A1A2A3A4外接球半径为R,点P是空间中任意一点.P到四面体A1A2A3A4外心的距离为d,则

当A1,A2,A3,A4,A5五点共球时,d=R,由定理10 可得:

推论3[7]空间中A1,A2,A3,A4,A5五点共球,对空间中任意一点P有

本文结果也可以看作是行列式应用的一个例子,行列式的更多应用可参见文献[6-7].

顺便指出:文献[7]中命题2 中的体积恒等式恰好搞反了符号! 应更正如下:

命题[7]O是空间中任意一点,则