对两道抛物线高考题的一点思考*
广东省中山市中山纪念中学(528454) 谢林涛
一、真题与解答
题目1(2018年高考浙江卷)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
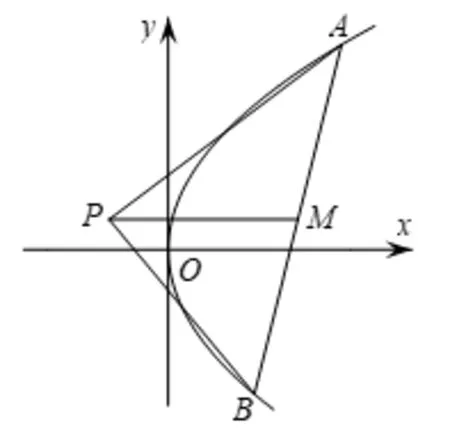
(Ⅰ)设AB中点为M,证明:PM垂直于y轴;
(Ⅱ)若P是半椭圆上的动点,求∆PAB面积的取值范围.
题目2(2021年高考乙卷理科)已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1 上点的距离的最小值为4.
(1)求p;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求∆PAB面积的最大值.
题目1 的解答(I)的方法1.设PA,PB的中点分别为D,E,设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),则两式相减得(y1+y2)(y1−y2)=4(x1−x2),所以直线AB的斜率.同理可得直线DE的斜率,因为AB//DE,所以kAB=kDE,因此y1+y2=y3+y4,所以AB中点M的纵坐标与DE中点M′的纵坐标相同,即MM′垂直于y轴,又P,M,M′三点共线,所以PM垂直于y轴.
(I)的方法2.设P(x0,y0),A(x1,y1),B(x2,y2),因为点A及PA的中点都在抛物线上,所以,再代入后式整理得因为点B及PB的中点都在抛物线上,同理可得所以y1,y2为方程的两个根,由韦达定理所以点M的纵坐标与点P的纵坐标相同,即PM垂直于y轴.
(II)由(I)可知
题目2 的解答(1)p=2(过程从略).(2)设P(x0,y0),A(x1,y1),B(x2,y2),易得切线PA的方程为y−y1=,将代入得同理切线PB的方程为又P(x0,y0)既在切线PA上,也在切线PB上,所以这说明A(x1,y1),B(x2,y2)两点都在直线上,即直线为直线AB,将其与x2=4y联立,整理得x2−2x0x+4y0=0,所以点P到直线AB的距离于是∆PAB面积在M:x2+(y+4)2=1 上,即故当y0=−5 时,S∆PAB取得最大值,最大值为.
将①的前式写成
评注经过计算,我们发现题目1 和题目2 中∆PAB面积的面积的表达式非常类似,于是笔者大胆猜测如果将题目1 中的“中点”和题目2 中的“切点”改为一般的“分点”,应该会有更一般的结论,下面分享笔者发现的拓展结论.
二、结论拓展
已知点P(x0,y0)是抛物线C:y2=2px外一点,A,B是抛物线C上不同的两点,AB的中点为M.
结论1若PA,PB的中点都在抛物线上,则PM垂直于y轴,且∆PAB的面积为.
结论2若PA,PB是抛物线的两条切线,A,B是切点,则PM垂直于y轴,且∆PAB的面积为.
结论3若直线PA与抛物线交于另外一点D,直线PB与抛物线交于另外一点E,且则PM垂直于y轴,且∆PAB的面积为.
结论4若直线PA与抛物线交于另外一点D,直线PB与抛物线交于另外一点E,且直线PM与抛物线交于点N,且抛物线在点N处的切线与直线PA,PB分别交于Q,R两点,则(1);(2)QR//AB;(3)∆PQR的面积为
结论5若PA,PB是抛物线的两条切线,A,B是切点,直线PM与抛物线交于点N,且抛物线在点N处的切线与直线PA,PB分别交于Q,R两点,则(1)N为PM的中点;(2)QR//AB;(3)∆PQR的面积为.
结论1 和结论2 的证明类似题1 和题2 的解答过程,本文不再赘述.
结论3 的证明方法1.设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),M(xM,yM).由定比分点坐标公式可知由D点在抛物线上,所以代入,整理得同理可得故y1,y2为方程的两个根,由韦达定理得所以yM=y0,PM垂直于y轴.
方法2.设A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),M(xM,yM),DE中点为M′,则两式相减得(y1+y2)(y1−y2)=2p(x1−x2),所以直线AB的斜率同理可得直线DE的斜率,因为AB//DE,所以kAB=kDE,因此y1+y2=y3+y4,所以AB中点M的纵坐标与DE中点M′的纵坐标相同,即MM′垂直于y轴,又P,M,M′三点共线,所以PM垂直于y轴.
∆PAB的面积
结论4 的证明由(3)知N点的纵坐标yN=y0,则N点的横坐标于是
对y2=2px两边对x求导得,2y·y′=2p,即所以切线QR的斜率直线AB的斜率kAB=因此kQR=kAB,即QR//AB.易知∆PQR∽∆PAB,相似比为,所以∆PQR的面积
类似地我们可以证明结论5,留给读者自行证明.
现在我们再回头去看高考题目1 和题目2.由结论3,当λ=1 时即为结论1 的结果,当λ →+∞时即为结论2 的结果.再由结论1,当p=2 时即可得到题目1 中的结果,由结论2,当p=2 即可得到题目2 的结果(交换x,y的位置).
三、备考建议
高考是一个选拔性考试,数学是高考选拔人才的重要学科,数学高考题越来越灵活多变,这就要求我们能够在灵活多变的表象下,透过表象看本质.在高考备考中,需要教师专研高考题,特别是同类的高考题,找到相似处,发现规律,揭露其数学本质,教师看清楚了题目的本质,学生才能做到举一反三,触类旁通.教师可以将数学阅读与写作引入课堂,改过去“讲练结合”为“讲练读写四结合”,优化课堂结构,指导学生做数学笔记(疑问性、感触性、梳理性笔记),提高学生的理解、转化、抽象、反思、归纳、建构、交流合作等能力,增进师生的情感交流,及时反馈,改进教学策略.学生具有一定数学写作能力有助于对数学知识的总结和内化,发现数学问题,进一步探究更多数学结论,也是一项必不可少的技能.更加有助于学生的自我监控和探究,专研学问,深化知识结构.

