2022年新高考I卷第22题的一题多解与推广
华南师范大学数学科学学院(510631) 陈俊阳
2022年新高考数学I 卷结构稳定,第22 题仍然是导数的应用问题.但与以往常规的以一个函数为主体的问题不同,该题考查了两个函数的最值问题以及它们图象与一条直线交点的问题,待证的结论也不再是以往具备套路性的极值点偏移问题,而是三个交点横坐标成等差数列.本题中两函数联系紧密,结构优美,结论也耐人寻味.
本文将从不同视角解答此题,并从不同的角度将问题进行推广,以期得到更一般的结论.
题目(2022年新高考I 卷第22 题)已知函数f(x)=ex−ax和g(x)=ax−lnx有相同的最小值.
(1)求a;
(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.
1 一题多解
问题的推广与变式离不开对解法的研究,因此本节将从不同视角解决上题,并从问题解决过程中探究问题的本质,进而对问题进行推广.第(1)问较为常规,下文仅给出简答.第(2)问需证明存在水平直线与两函数图象有三个交点以及交点横坐标依次成等差数列,下文的将分别讨论它们的两个不同解法.
1.1 第(1)问解答求导易得f(x)在(−∞,lna)单调递减,在(lna,+∞)单调递增;g(x)在单调递减,在单调递增,利用最值相等即可求得a=1.
1.2 第(2)问:三个交点存在性的证明由(1)知,f(x)在(−∞,0)单调递减,在(0,+∞)单调递增,g(x)在(0,1)单调递减,在(1,+∞)单调递增,从而y=b与它们至多只有四个交点.当b≤1 时,y=b与它们至多只有两个交点,不合题意.当b>1 时,由于x →∞时,f(x)→+∞;x →0+和x →+∞时,g(x)→+∞,故y=b与y=f(x)和y=g(x)均有两个交点.
令h(x)=f(x)−g(x)=ex+ lnx−2x,h′(x)=所以h(x)在(0,+∞)单调递增.又所以h(x)在(0,+∞)有且仅有一个零点x0∈(e−2,1),从而y=f(x)与y=g(x)的图象有且仅有一个交点(x0,y0).因此,取b=y0得,y=b与y=f(x)和y=g(x)共有三个不同的交点,证毕.
1.3 第(2)问:等差数列的证明
记三交点的横坐标从左到右分别为x1,x0,x2,满足f(x1)=f(x0)=g(x0)=g(x1)=b,且有x0−lnx0=b.
1.3.1 视角1:f(x),g(x)结构的相似性
观察f(x)=ex−x,g(x)=x−lnx的结构注意到:f(lnx)=g(x),g(ex)=f(x). 而x0是两函数交点的横坐标,因此,考虑用x0作为桥梁,表示x1,x2,往证:x1+x2=lnx0+.
解法1由于f(x1)=g(x0)=f(lnx0)=b,且方程f(x)=b有且仅有两个解x=x1或x0,因此lnx0=x1或x0,若lnx0=x0,则b=x0−lnx0=0,舍去.因此x1=lnx0.由于g(x2)=f(x0)==b,同理可得所以证毕.
1.3.2 视角2:考虑x1,x2 与x0 的距离
若学生观察不出f(x),g(x)结构的相似性,则分别求出x1,x2与x0的距离,证明它们是相等的,即得三者成等差数列.
解法2一方面,设x1=x0−n,n >0,由f(x0)=f(x1)=f(x0−n)得从而
另一方面,设x2=x0+m,m >0,同理可得m=b,从而x2=x0+b.所以证毕.
1.3.3 视角3:先猜后证
画出f(x),g(x),y=b的草图后,注意到x1,x2与x0的距离相等,且等于b,于是猜测x1=x0−b,x2=x0+b,因此只需证明f(x0−b)=f(x0),g(x0+b)=g(x0).
解法3一方面,由于
故f(x0−b)=f(x0). 又方程f(x)=b有且只有两个解x1,x0,故x0−b=x0或x1,又因为b>1,所以
另一方面,由于
故g(x0+b)=g(x0).同理可得
综合②③可得,x1+x2=2x0,证毕.
1.3.4 视角4:无字证明
解法4由图1 易见,当BC⊥x轴时,y=b与曲线y=f(x),y=g(x)共有三个不同的交点.又由反函数的对称性知四边形ABCD为矩形,故A,D到BC的距离相等,即x0−x1=x2−x0,从而原命题得证.
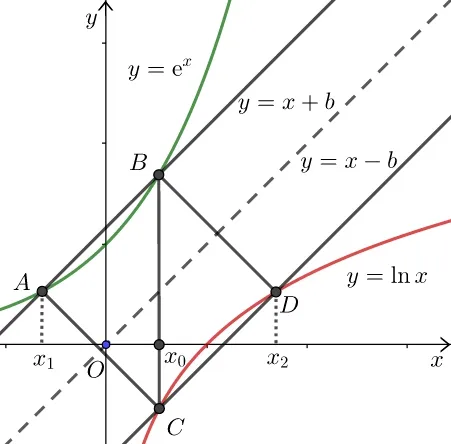
图1
这样的“无字证明”从直观上揭示了本题优美的几何背景,但几何直观在逻辑推理中缺乏思维的严谨性,无法取代代数的合理运算过程[1].因此,从几何直观的视角解决本题仍需结合严谨的代数运算分四步进行证明:(1)结合y=ex,y=lnx的凹凸性,证明当b>1 时,y=x+b,y=x−b分别与y=ex,y=lnx有两个不同的交点;(2)通过证明方程ex+lnx−2x=0 有唯一解(2.1 的做法)得到存在b>1,使得BC⊥x轴;(3)利用反函数的特征,证明两互为反函数图象对应的交点也关于y=x对称,从而得到四边形ABCD为矩形;(4)最后利用矩形的性质即证得原命题.
2 问题的推广
首先,b的不同取值,决定了交点个数的不同,那么当y=b与y=f(x)和y=g(x)共有四个交点时,四个点的横坐标是否也有类似的等量关系?
其次,如果将f(x)=ex−x,g(x)=x−lnx差的结构变为商的形式,结论会不会从等差数列变为等比数列呢?
再者,f(x),g(x)两函数的结构相似,成立f(lnx)=g(x),g(ex)=f(x)的原因是y=ex与y=lnx互为反函数,y=x正是它们的对称轴,因此,如果将y=ex,y=lnx换成互为反函数的两个函数,结论是否仍然成立? 下面将围绕着这三个问题展开探究.
2.1 视角1:交点个数
下面从交点个数的视角对问题进行推广.首先考虑三者交点个数的所有情况,并针对四个交点的情形探究它们横坐标之间的关系.于是得到:
推广1设f(x)=ex−x,g(x)=x−lnx,记y=b与y=f(x),y=g(x)的交点个数为α,则y=f(x)与y=g(x)有唯一交点(x0,y0),并且当b <1 时,α=0;当b=1 时,α=2;当b=y0时,α=3;当b>y0或1 推广2直线y=b与f(x)=ex−x和g(x)=x−lnx分别交于(x1,b),(x2,b)(x1 证明由f(x1)=g(x4)=f(lnx4),且方程f(x)=b有且仅有两个解x=x1或x2,故lnx4=x1或x2.同理可得lnx3=x1或x2.又x1 进而x3−x1=x4−x2,即x1+x4=x2+x3,证毕. 注将交点个数从3 推广到4 后发现,原题第(2)问的结论是推广2 的退化形式(即x2=x3). 和差与积商通常对应着等差与等比,所以下面将函数变为商的结构,结论也相应变为等比数列: 推广3直线分别交于(x1,b),(x2,b)(x1 证明因为直线交于(x1,b),(x2,b)两点,从而进而又由于f(lnx)=g(x),f(x)=g(ex),故与推广2 的证明同理可得即x1x4=x2x3,证毕. 当其中两点重合时,得到与原命题对偶的命题: 推论1直线从左到右交于(x1,b),(x2,b),(x3,b)三点,则x1,x2,x3成等比数列,即 2.3.1 将y=ex,y=lnx 推广为一般函数φ(x) 互为反函数的两函数复合是恒等映射,即φ[φ−1(x)]=x.于是设f(x)=φ(x)−x,g(x)=x−φ−1(x),也能得到同样的结论: 推广4设f(x)=φ(x)−x,g(x)=x−φ−1(x).若存在直线y=b,使之与y=f(x)和y=g(x)的图象均有两个交点,且在y=b这一水平高度处,y=f(x)与y=g(x)有唯一的公共点(x0,b)(其中φ(x0)x0),则此时直线y=b与y=f(x)和y=g(x)的图象共有三个交点,且x0是另外两交点横坐标的等差中项. 证明设另外两个交点的横坐标为x1,x2,满足f(x1)=f(x0)=g(x0)=g(x2)=b,且由f(x0)=g(x0)得φ(x0)−x0=x0−φ−1(x0),即 而f(x),g(x)满足f(x)=φ(x)−x=φ(x)−φ−1[φ(x)]=g[φ(x)],同理g(x)=f[φ−1(x)]. 由于b=f(x1)=g(x0)=f[φ−1(x0)],而方程f(x)=b有且只有两个解x=x1或x0,又φ(x0)x0,故φ−1(x0)̸=x0,从而 另一方面b=g(x2)=f(x0)=g[φ(x0)],同理可得 结合④∼⑥可得x1+x2=2x0,证毕. 对于四个交点的情形,也有同样的结论: 推广5直线y=b与f(x)=φ(x)−x和g(x)=x−φ−1(x)分别交于(x1,b),(x2,b)(x1 证明与推广4 同理可得f(x)=g[φ(x)],g(x)=f[φ−1(x)]. 由于f(x1)=g(x3)=f[φ−1(x3)],方程f(x)=b有且仅有两个解x=x1或x2,故φ−1(x3)=x1或x2.同理可得φ−1(x4)=x1或x2.又x1 注推广4 是推广5 的退化形式(即x2=x3). 推广6直线分别交于(x1,b),(x2,b)(x1 证明与推广3 和推广5 的证明同理,略. 2.3.2 将y=x 推广为一般的一次函数y=kx+m 由于y=x恰为两互为反函数的函数图像的对称轴,进一步将f(x)=φ(x)−x的第二项x推广为一般的一次函数y=kx+m,则得到更一般的结论: 推广7设f(x)=φ(x)−kx−m,g(x)=x−kφ−1(x)−m.若存在直线y=b,使之与y=f(x)和y=g(x)的图象均有两个交点,且在y=b这一水平高度处,y=f(x)与y=g(x)有唯一的公共点(x0,b)(其中φ(x0)x0),则此时直线y=b与y=f(x)和y=g(x)图象的三个交点x1,x0,x2满足kx1+x2=(k+1)x0. 证明由于f(x)=g[φ(x)],g(x)=f[φ−1(x)],与推广3 的同理可得x1=φ−1(x0),x2=φ(x0). 又由f(x0)=g(x0)得φ(x0)+kφ−1(x0)=(k+ 1)x0,从而kx1+x2=(k+1)x0,证毕. 注推广4 是推广7 的特殊情形(k=1). 推广8直线y=b与f(x)=φ(x)−kx−m,g(x)=x−kφ−1(x)−m分别交于(x1,b),(x2,b)(x1 证明与推广7 的证明类似,略. 注推广8 是推广2,4,5,7 的最一般形式. 以上不同的解法与推广从不同的视角揭示了本题的背景与本质,最终给出一般性的结论,这为模拟题命制与变式教学提供了丰富的素材,也提供了数学问题研究的一种范式. 此外,读者还可以进一步探究:(1)当y=b与f(x)=φ(x)−x和g(x)=x−φ−1(x)有四个不同交点时,除了x1+x4=x2+x3,其横坐标之间存在哪些具备优美对称性的等量或不等关系?(2)设f(x)=φ(x)−x+m(x),g(x)=x−φ−1(x)+n(x),当m(x)与n(x)满足什么条件时,也能得到哪些具备优美对称性的对称等量或不等关系?(3)如果改变函数的具体表达式或结构,使交点个数进一步推广到n或2n,能否仍然得到类似的结论?(4)若两函数y=α(x)与y=β(x)关于直线y=kx+b(k ̸=0)对称,再用一条水平直线(或一般直线)去截曲线f(x)=α(x)−(kx+b)与g(x)=kx+b−β(x),所得交点的横坐标有没有类似的结论? 若没有,那么f(x),g(x)的表达式应如何调整,才有具有对称美的等量或不等关系?2.2 视角2:函数结构变式
2.3 视角3:函数一般化
3 研究展望

