地铁建设对公交系统鲁棒性的影响

林兆丰 李树彬 孔祥科

摘要：为提高城市公交系统的鲁棒性，制定了基于换乘的加边策略。以济南市公交-地铁复合网络为例，研究了网络的特性参数和鲁棒性，并提出基于换乘的加边策略提高网络鲁棒性。研究表明：复合网络具有小世界和无标度网络特性；网络在蓄意攻击下比随机攻击更具脆弱性；在介数攻击下，高度加边策略对网络鲁棒性提升较为显著，使网络瘫痪时被攻击站点比例提升50.46%；在随机攻击和度攻击下，高介数加边策略对网络鲁棒性提升较为显著，使被攻击站点比例分别提升23.35%和39.81%。

关键词：复杂网络；公交-地铁复合网络；鲁棒性分析；加边策略

中图分类号： U121文献标识码： A

收稿日期：2021-09-03；修回日期：2021-10-26

基金项目：国家自然科学基金（71871130，71771019，71971125）；山东省公安厅科技服务项目（SDGP370000000202102003878，SDGP3700000002021 02003700）

第一作者：林兆丰（1998-），男，福建漳州人，硕士研究生，主要研究方向为复杂网络研究、智能交通系统。

通信作者：李树彬（1977-），男，山东聊城人，博士，教授，主要研究方向为交通流理论、复杂网络研究、智能交通系统。

The Influence of Subway Construction on the Robustness of Public Transportation System

LIN Zhaofeng¹， LI Shubin^1，2， KONG Xiangke¹

（1. School of Transportation Engineering， Shandong Jianzhu University， Ji′nan 250101， China;

2. Department of Traffic Management Engineering， Shandong Police College， Ji′nan 250014， China）

Abstract：To improve the robustness of urban public transport system， an edge adding strategy based on transfer is formulated. Take the bus-subway composite network in Jinan as an example， the characteristic parameters and robustness of the network are studied， and an edge adding strategy based on transfer is proposed to improve the network robustness. The research shows that the composite network has the characteristics of small world and scale-free network; The network is more vulnerable than random attack under intentional attack; The network robustness is improved significantly by the high-degree edge addition strategy under betweenness attacks， which increases the proportion of attacked stations by 50.46% when the network is paralyzed; The network robustness is improved significantly by the high-betweenness edge addition strategy under random attacks and degree attacks， which increases the proportion of attacked stations by 23.35% and 39.81% respectively.

Key words： complex network; bus-subway composite network; robustness analysis; edge adding strategy

0 引言

城市公共交通系統作为城市基础设施的重要组成部分，在城市的社会、经济发展中发挥着重要的作用，然而城市公共交通系统时常受到自然灾害、交通事故等事件的影响，造成某些站点故障、线路停运，甚至网络的大规模瘫痪。因此，如何保证城市公共交通系统的安全运营，对居民安全出行和提高运输效率具有重要意义。近年来，随着复杂网络的兴起，其理论也为广大交通网络研究者提供了全新的视角。

在鲁棒性方面，Cao等^[1]对长沙市公交网络进行静态与动态抗毁性仿真，进而识别网络中的关键站点。Li等^[2]对重庆市公交-地铁复合网络进行对比研究，发现层间耦合可以提高复合网络的鲁棒性。Huang等^[3]提出基于流量分配的耦合映像格子（Coupled Map Lattice，CML）模型，对比了北京市公交-地铁复合网络与公交网络的鲁棒性差异，发现动态重分配可以显著提高网络面对随机攻击的容忍度。Ma等^[4]基于流量分配的CML模型模拟了西安市公交-地铁复合网络在暴雨条件下的网络鲁棒性，并定量化暴雨强度与攻击程度的关系。张琳等^[5]提出了考虑公交、地铁站点间的容忍度差异的耦合规则，对南京市公交-地铁相依网络进行鲁棒性分析。宋英华等^[6]对比了武汉市公交-地铁复合网络在不同耦合半径下的网络鲁棒性。在鲁棒性优化方面，Liu等^[7]提出多模式公交网络的动态弹性评估方法，研究站点恢复对网络鲁棒性的影响。Zhang等^[8]提出地铁网络弹性评价的通用框架，研究上海地铁网络遭受攻击后的站点和线路的最佳恢复顺序和时间。王非^[9]通过增减站点和设置实际约束构建公交网络优化模型。赖强^[10]等采用高度数加边、高介数加边、低度数加边、低介数加边和随机加边5种策略对公交网络进行鲁棒性优化对比，研究发现低度数加边和低介数加边策略对鲁棒性提高更明显。刘美玲^[11]采用随机加边、最小介数之和加边及最小度之和3种加边策略对高速铁路网进行鲁棒性优化对比。

现有关于加边策略优化公共交通网络鲁棒性的研究主要从网络的拓扑特性视角出发，未考虑加边是否具有合理性和实用性，可能导致相距较远的站点存在不合理的线路。基于此，文章以济南市公交-地铁复合网络为例，研究济南市公交-地铁复合网络的网络特性参数和在不同攻击策略下的网络鲁棒性，并依据仿真结果，提出合理性和实用性的高度值加边和高介数加边策略优化网络鲁棒性，为济南市公共交通网络安全运营及科学化管理提供一定参考依据。

1 网络模型构建

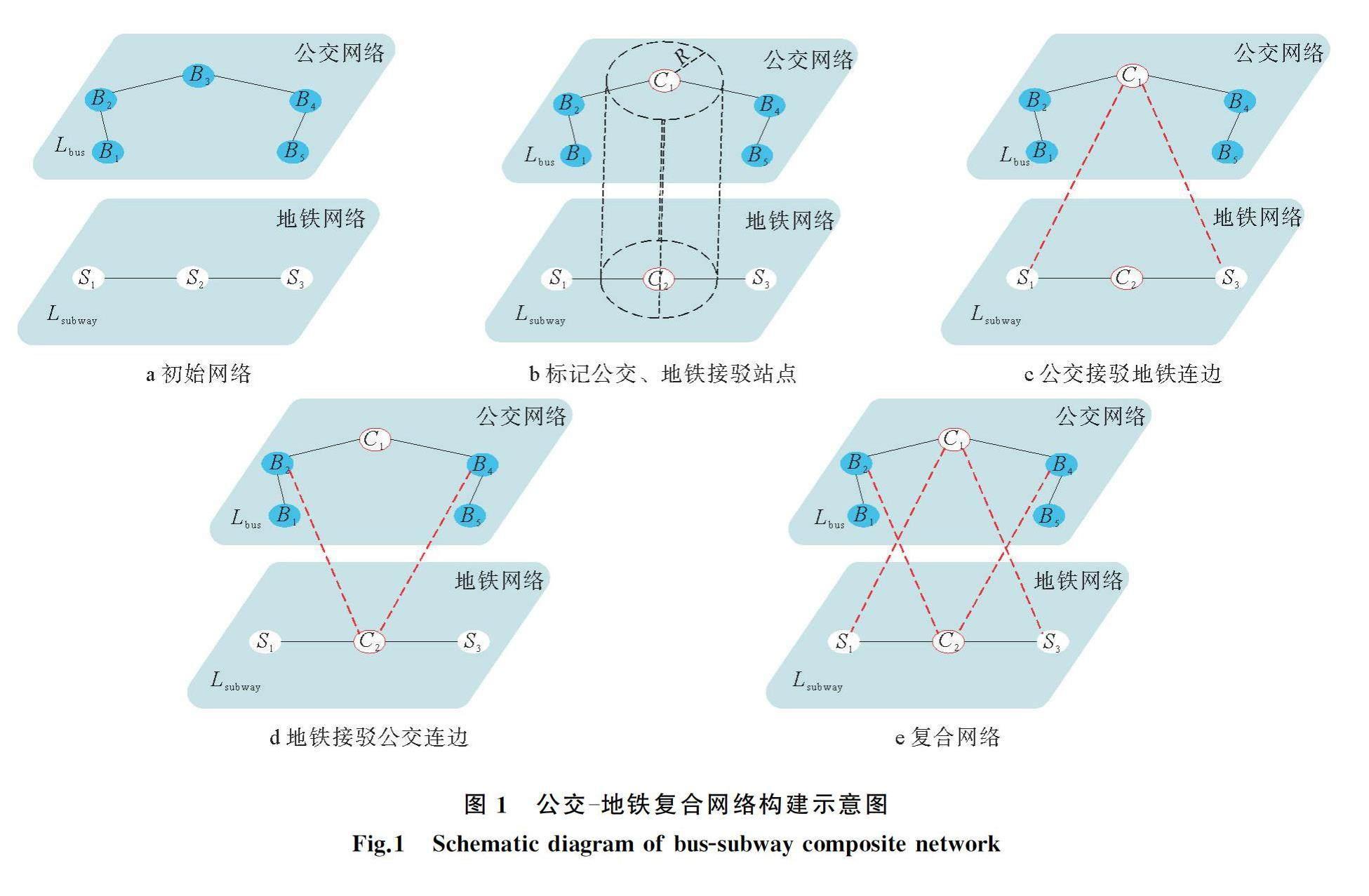
文章采用文献[9]和[12]提出的公交-地铁复合网络（Space-L）构建方法构建网络，构建说明如下：

1）构建公交网络，包括公交线路L_bus，站点B₁，B₂，B₃，B₄，B₅。构建地铁网络，包括地铁线路L_subway，站点S₁，S₂，S₃，如图1a所示。

2）将公交、地铁站点间距离小于500 m视为存在接驳关系^[13-15]。公交站点B₃与地铁站点S₂相距在500 m范围内，即两者存在接驳关系，并进行标记为C₁，C₂，如图1b所示。

3）公交站点C₁与其接驳的地铁站点C₂相邻，换乘距离较短，故公交站点C₁将继承地铁站点C₂的邻居站点S₁，S₃，建立公交接駁地铁连边（C₁，S₁），（C₁，S₃），如图1c所示。

4）地铁站点C₂为公交站点C₁相邻的接驳地铁站点，故地铁站点C₂将继承公交站点C₁的邻居站点B₂，B₄，建立地铁接驳地铁连边（C₂，B₂），（C₂，B₄），如图1d所示。

5）构建完的公交-地铁复合网络，如图1e所示。

2 网络特性及鲁棒性度量指标

2.1 网络特性

2.1.1 度k_i与度分布P（k）

站点度k_i定义为站点i与相邻站点连边数目之和，如式（1）所示，常用度分布函数P（k）描述站点度的分布情况。

其中，若站点i与j连通，则a_ij=1，否则，a_ij=0。

2.1.2 介数B_i

站点介数B_i定义为网络中所有最短路径中经过站点i的比例，如式（2）所示。

其中，n_ij（i）为站点j与k的最短路径经过站点i的数目，n_jk为站点j与k的最短路径的总数，

2.1.3 聚类系数C_i

站点聚类系数C_i定义为站点i的邻居站点之间实际存在的边数E_i与最大可存在边数之比，如式（3）所示。

2.1.4 平均最短路径L

平均最短路径L定义为任意两个站点之间距离的平均值，如式（4）所示。

其中，N为网络的总站点数，d_ij为站点i与j间的最短距离。

2.2 鲁棒性度量指标

2.2.1 网络效率E

网络效率E用来衡量站点间的传输效率。当网络遭受攻击后，站点间的最短路径长度增大，站点间的传输效率降低。定义为所有最短路径长度的倒数之和与总最短路径数的比值，如式（5）所示。

2.2.2 网络最大连通率S

网络最大连通率S是衡量网络的整体连通性的一个常用指标。当网络遭受攻击后，网络分离为多个子图或孤立站点，含有站点数量最多的子图称为最大连通子图，其所含站点数量N′与初始网络总站点数量N的比称为网络最大连通率，如式（6）所示。

3 实例分析

本文数据来源于济南公交公司集团，选取2021年4月济南市334条公交线路、3条地铁线路、2 572个公交站点、40个地铁站点为样本数据，采用基于Space-L方法的复合网络构建方法构建济南市公交-地铁复合网络，建模时将上下行线路、站点抽象成无向无权网络，网络共计2 612个网络节点，4 271条网络边，借助Gephi可视化网络，如图2所示。

3.1 公交-地铁复合网络特性分析

3.1.1 度与度分布

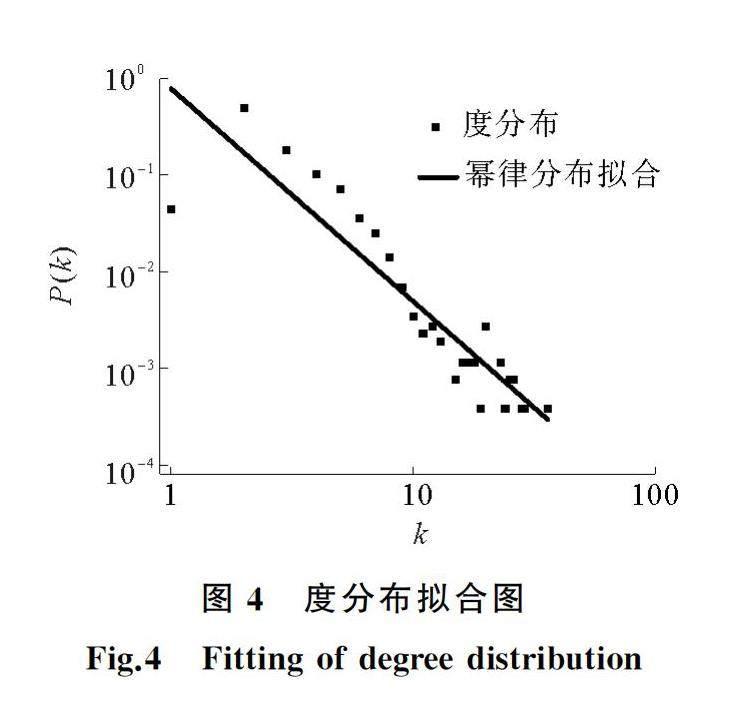
由图3可知，复合网络平均度为3.27，表明每个站点平均与3～4个站点相邻。度值为2的站点所在比例最大，为49.69%，度值大于7的站点所占比例不足1%，表明网络中的站点连接较为稀疏，只有少量的站点承担着网络的合流、分流作用，一般为枢纽或集散站点。由图4可知，对网络度分布在双对数坐标轴下进行拟合，拟合结果满足线性回归方程y=－2.203x－0.238 1，R²=0.883 8，表明度分布符合幂律分布，满足Barabasi和Albert提出的大部分的节点具有较小的度，少量节点具有较大的度，且度分布满足幂律分布的无标度网络特性^[16]，因此网络具有无标度网络特性。

3.1.2 介数

由图5可知，复合网络中绝大多数的站点介数很小，且分布较为集中，网络中92%的站点介数小于0.02，其中有183个站点介数等于0，有10个站点介数大于0.1，这表明站点介数的分布较为均匀，对网络重要性影响的差异性不大，仅存在少量对网络重要性影响较大的站点。

3.1.3 聚类系数与最短路径

由图6可知，复合网络平均聚类系数为0.133，这表明网络的平均聚类系数较大，当网络中的某个站点遭受攻击时，对原有直达的站点间的连接不会有太大的影响，网络具有较高的容忍度。由图7可知，网络平均最短路径长度为17.526，表明从起始点出发平均需经过17～18个站点到达其目的地。图像基本符合泊松分布，平均值右半部分大于左半部分，表明一半以上的节点间最短路径长度偏大，网络有效性偏低。网络直径为60，即网络中站点间最远距离（舜兴路与安康路交叉口站点到断岧村站点之间）需经过60个站点。根据Watts和Strogatz提出的小世界网络的衡量规则^[17]，生成同等规模随机网络，得出网络的平均最短路径长度与平均聚类系数均大于同规模随机网络，说明网络具有小世界网络特性。

3.1.4 公交-地铁复合网络与子网络的网络特性综合对比

由表1可知，复合网络平均度和聚类系数高于公交网络，表明地铁站点的加入，使站点间的联系更为紧密。复合网络平均路径长度小于公交网络，表明居民出行采用公交与地铁配合出行方式相比单独使用公交出行方式更为便利。复合网络与公交网络直径相等，主要由于济南市地铁网络规模较小，且大部分未经过城市中心，因而复合网络的直径所在路径仅经过公交站点，而未经过地铁站点，因此与公交网络最远距离线路一致。

3.2 公交-地鐵复合网络鲁棒性分析

鲁棒性是指网络在某种因素的破坏或影响下，保持正常运营的能力，也称静态抗毁性。本文采用随机攻击和蓄意攻击作为攻击策略，其中蓄意攻击为度攻击和介数攻击，以网络效率和网络最大连通率作为判断依据，研究对比公交-地铁复合网络与公交网络鲁棒性的差异。蓄意攻击策略：依据度或介数排名，每次攻击网络5%的站点，直至网络完全瘫痪后终止。随机攻击策略：依据Matlab中的Randi函数生成随机序列，依次攻击网络5%的站点，直至网络完全瘫痪后终止，并独立运行50次，取50次运行结果的平均值。仿真结果如图8～10所示。

由图8～10可知，复合网络曲线数值在两种度量指标上均位于公交网络之上，复合网络初始E=0.077，相比于公交网络初始E=0.070，提升了10.3%，这表明复合网络由于地铁站点的加入，其鲁棒性在3种攻击策略下均优于公交网络。由图8可知，在随机攻击下，复合网络和公交网络E和S下降较为缓慢，当随机故障的站点比例为10%时，网络仍具有较高的鲁棒性（E=0.044，0.037，S=0.741，0.702），这表明当随机故障的站点比例较少时，对网络的整体运行能力影响较小。当随机故障的站点比例为30%时，网络基本无法满足正常的运行能力（E=0.014，0.009，S=0.397，0.320），这表明随着随机故障站点比例的增加，仍会对网络鲁棒性产生较大影响。由图9可知，在度攻击下，复合网络和公交网络E和S呈现出由激剧下降后趋于平缓，当被攻击站点比例为20%时，网络基本处于完全瘫痪（E=0.003，0.002，S=0.120，0.047），这表明在攻击初期，被攻击的站点多为网络中的“换乘站点”、“枢纽站点”等高度值站点，对网络的整体传输效率和连通性有致命性的破坏，在攻击后期，被攻击的站点多为网络中的“边缘站点”，对网络的稳定性无较大影响。由图10可知，在介数攻击下，复合网络和公交网络E和S呈现出由快速下降后趋于平缓，下降趋势介于随机攻击与度攻击之间，当攻击站点比例为20%时，网络接近完全瘫痪状态（E=0.010，0.007，S=0.397，0.333），这表明在攻击初期，被攻击的站点多为网络中的“桥梁站点”，对网络的鲁棒性有致命性的破坏。

综上所述和对比图8a至图10a，图8b至图10b可知，复合网络和公交网络对随机攻击络具有较强的鲁棒性，对蓄意攻击具有脆弱性，其中度攻击下的破坏最为显著。究其原因：两者网络均具有无标度网络特性，其站点是异质的，基于度的蓄意攻击对网络异质性的影响最大。

3.3 鲁棒性优化

3.3.1 加边策略

网络加边是提高网络鲁棒性的常用手段^{[10-11，18-20]}，若未考虑加边在交通网络中是否具有合理性和实用性，可能导致相距较远的站点存在不合理的线路，因此本文基于公交、地铁的换乘角度提出高度、高介数加边两种策略，加边策略示意图如图11所示。

由图11a可知，线路调整前存在公交线路L₁，站点B₁，B₂，B₃，地铁站点S的500 m服务半径内的B₄，B₅两个公交站点。由图11b可知，公交线路L₁的B₂站点处于地铁站点S的500～1 500 m范围内，公交站点B₄位于地铁站点S的服务半径内且距离公交站点B₂最近，故将原有公交线路走向B₁，B₂，B₃就近调整为B₁，B₄，B₂，B₃。由图11c可知，线路调整后，地铁站点S将继承公交站点B₄的邻居站点B₁，B₂，建立连边（S，B₁），（S，B₂）。通过该线路的调整，能保持原有线路大体走向，避免大规模线路调整影响原有居民公交出行路径，同时提高公交、地铁的换乘路径选择。

1）高度加边策略（HDA）：计算复合网络中各站点度；按度由高到低依次选择出地铁站点S₁，以其作为中心的500～1 500 m半径内依次选择出大于等于公交网络的平均度的公交站点B₁，并选择出距离公交站点B₁最近且在地铁站点500 m服务半径内的公交站点B₂，同时改变线路的邻接关系，并连接地铁站点S与公交站点B₂的邻居站点，不允许出现重边情况，直至到规定的加边数停止。

2）高介数加边策略（HBA）：计算复合网络中各站点度；按介数由高到低依次选择出地铁站点S₁，以其作为中心的500～1 500 m半径内依次选择出大于等于公交网络的平均介数的公交站点B₁，并选择出距离公交站点B1最近且在地铁站点500 m服务半径内的公交站点B₂，同时改变线路的邻接关系，并连接地铁站点S与公交站点B₂的邻居站点，不允许出现重边情况，直至到规定的加边数停止。

为控制加边数一致，需先单独运行两次仿真，确定两种策略的加边数，取两者的最小边数作为规定加边数。

3.3.2 鲁棒性优化实例分析

本文通过Python编程语言编写两种仿真加边策略，采用随机攻击和蓄意攻击作为攻击策略，其中蓄意攻击为度攻击和介数攻击，以网络效率和网络最大连通率作为判断依据，以复合网络作为对比网络，研究两种加边策略对网络鲁棒性的影响，仿真结果如图12～14所示。

由图12～14可知，HDA策略、HBA策略E和S曲线均位于初始曲线之上，HDA策略对初始E由0.077提高到0.090，提升了15.6%，HBA策略提升了12.5%，表明两种加边策略均能很好地提高网络鲁棒性。由图12可知，在随机攻击下，以E为衡量指标，HBA策略网络有效性优于HDA策略，HDA策略使网络瘫痪攻击站点比例由35.07%

提高到41.02%，提升率为16.97%；HBA策略使网络瘫痪站点比例由35.07%提高到43.26%，提升率为23.35%。以S为衡量指标，HDA策略使网络瘫痪站点由47.77%提高到56.69%，提升率为18.67%。HBA策略由47.77%提高到59.11%，提升率为23.74%。由图13可知，在度攻击下，以E为衡量指标，HBA策略在整体上网络有效性优于HDA策略。HDA策略使网络瘫痪时站点比例由13.84%提高到18.45%，提升率为33.31%。HBA策略使网络崩溃站点比例由13.84%提高到19.35%，提升率为39.81%。以S为衡量指标，HDA策略使网络瘫痪站点由22.33%提高到27.18%，提升率为17.84%。HBA策略由22.33%提高到28.56%，提升率为27.90%。由图14可知，在介数攻击下，以E为衡量指标，HDA策略在提高网络有效性方面优于HBA策略。当网络瘫痪时，HDA策略及HBA策略两者对应的被攻击站点比例分别为30.77%，28.63%，较复合网络站点比例20.45%，分别提升了50.46%，40%。以S为衡量指标，当网络瘫痪时，HDA策略、HBA策略两者对应的被攻击站点比例分别为48.52%，51.33%，较复合网络站点比例44.43%，提升率分别为9.21%，15.53%。

综上所示，HBA策略、HDA策略较复合网络在网络有效性及网络最大连通子图上均有明显提升。HBA策略在随机攻击下及度攻击下鲁棒性提高优于HDA策略，HDA策略在介数攻击下鲁棒性提高优于HBA策略。HBA策略较好。

4 结论

本文以Space-L方法构建济南市公交-地铁复合网络，首先系统地研究了网络统计特性参数。其次，对复合网络和公交网络进行鲁棒性分析。最后，给出考虑实际交通情况下的加边策略优化鲁棒性。得到以下主要结论：济南市公交-地铁复合网络具有无标度網络特性和小世界特性；复合网络及公交网络在蓄意攻击下较随机攻击下更具脆弱性，因此交通管理部门有必要对重要性站点进行重点保护，做好相应的应急方案；HBA策略、HDA策略对网络鲁棒性均有明显提升。HBA策略在随机及度攻击下鲁棒性提升优于HDA策略。HDA策略在介数攻击下优于HBA策略，同时该加边策略具有较好的经济性和实用性，对城市的规划和管理有一定启示作用，未来可将网络鲁棒性和鲁棒性优化理念融入城市交通规划中。此外，本文研究仅从无权无向网络出发，未考虑客流量，发车频率等情况，今后，将针对不足之处进行深入研究。

参考文献：

[1]CAO N， CAO H Q. Exploring the robustness of urban bus network： a case from Southern China[J]. Chinese Journal of Physics， 2020， 65（1）：389-397.

[2]LI X H， GUO J Y， GAO C， et al. Network-based transportation system analysis： a case study in a mountain city[J]. Chaos， Solitons and Fractals： the Interdisciplinary Journal of Nonlinear Science， and Nonequilibrium and Complex Phenomena， 2018， 107（1）：256-265.

[3]HUANG A L， ZHANG H M， GUAN W， et al. Cascading failures in weighted complex networks of transit systems based on coupled map lattices[J]. Mathematical Problems in Engineering， 2015（1）：1-16.

[4]MA F， LIU F， YUEN K F， et al. Cascading failures and vulnerability evolution in bus-metro complex bilayer networks under rainstorm weather conditions[J]. International Journal of Environmental Research and Public Health， 2019， 16（3）：329-329.

[5]张琳， 陆建， 雷达. 基于复杂网络和空间信息嵌入的常规公交-地铁复合网络脆弱性分析[J]. 东南大学学报（自然科学版）， 2019， 49（4）：773-780.

ZHANG L， LU J， LEI D. Vulnerability analysis of bus-metro composite network based on complex network and spatial information embedding[J]. Journal of Southeast University（Natural Science Edition）， 2019， 49（4）：773-780.

[6]宋英华， 李玉枝， 霍非舟， 等. 城区内涝条件下城市公交-地铁双层交通网络的脆弱性分析[J]. 安全与环境工程， 2021， 28（2）：114-120.

SONG Y H， LI Y Z， HUO F Z， et al. Vulnerability of two-layer traffic network of bus and subwayunder waterlogging condition based on complex network theory[J]. Safety and Environmental Engineering， 2021， 28（2）：114-120.

[7]LIU Z Z， CHEN H， LIU E Z， et al. Evaluating the dynamic resilience of the multi-mode public transit network for sustainable transport[J]. Journal of Cleaner Production， 2022， 348（1）：131350.

[8]ZHANG D M， DU F， HUANG H W， et al. Resiliency assessment of urban rail transit networks： Shanghai metro as an example[J]. Safety Science， 2018， 106（1）：230-243.

[9]王非. 基于复杂网络的公交线网特性分析与优化研究[D]. 北京： 北京交通大学， 2020.

WANG F. Research on the characteristics analysis and optimization of transit transportation network based on complex network theory[D]. Beijing： Beijing Jiaotong University， 2020.

[10]赖强， 张宏昊， 王徐盱. 基于复杂网络理论的城市公交网络鲁棒性分析与优化[J]. 计算机工程与应用， 2022， 58（10）：249-254.

LAI Q， ZHANG H H， WANG X X. Robustness analysis and optimization of urban public transport network based on complex network theory[J]. Computer Engineering and Applications， 2022， 58（10）：249-254.

[11]劉美玲. 基于复杂网络理论的我国高速铁路网络抗毁性研究[D]. 北京： 北京交通大学，2019.

LIU M L. Invulnerability research of China high-speed railway network based on complex network theory[D]. Beijing： Beijing Jiaotong University， 2019.

[12]鲍登， 高超， 张自力. 基于复杂网络的公交-地铁复合网络鲁棒性分析[J].西南师范大学学报（自然科学版）， 2017， 42（5）：22-27.

BAO D， GAO C， ZHANG Z L. Analysis robustness of bus and subway interdependent network based on complex network theory[J]. Journal of Southwest China Normal University（Natural Science Edition）， 2017， 42（5）： 22-27.

[13]ZHANG L， WEN H Y， LU J， et al. Exploring cascading reliability of multi-modal public transit network based on complex networks[J]. Reliability Engineering & System Safety， 2022， 221（1）：108367.

[14]沈犁， 张殿业， 向阳， 等. 城市地铁—公交复合网络抗毁性与级联失效仿真[J]. 西南交通大学学报， 2018， 53（1）：156-163，196.

SHEN L， ZHANG D Y， XIANG Y， et al. Simulation on survivability and cascading failure propagation of urban subway-bus compound network[J]. Journal of Southwest Jiaotong University， 2018， 53（1）：156-163，196.

[15]曲迎春， 徐仲之， 龚航，等. 城市轨道交通网络脆弱性分析[J]. 铁道科学与工程学报， 2016， 13（11）：2276-2283.

QU Y C， XU Z Z， GONG H， et al. Vulnerability analysis of urban rail transit networks[J]. Journal of Railway Science and Engineering， 2016， 13（11）：2276-2283.

[16]BARABASI A L， ALBERT R. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）：509-512.

[17]WATTS D J， STROGATZ S H. Collective dynamics of small-world networks[J]. Nature， 1998， 393（6684）：440-442.

[18]劉涤尘， 冀星沛， 陈果， 等. 基于复杂网络理论的电力通信网加边保护策略[J]. 电力自动化设备， 2016， 36（10）：121-126.

LIU D C， JI X P， CHEN G， et al. Link addition strategy based on complex network theory for power communication network[J]. Electric Power Automation Equipment， 2016， 36（10）：121-126.

[19]张洁. 基于复杂网络理论的电力通信网扩容保护策略研究[D]. 北京： 华北电力大学（北京）， 2019.

ZHANG J. Research on capacity expansion and protection strategy of power communication network based on complex network [D]. Beijing： North China Electric Power University （Beijing）， 2019.

[20]赵焱鑫， 李黎， 王小明. 复杂网络加边扩容策略研究[J]. 计算机应用研究， 2015， 32（6）：1839-1841.

ZHAO Y X， LI L， WANG X M. Effective strategy of adding links for maximizing traffic capacity of complex networks[J]. Application Research of Computers， 2015， 32（6）： 1839-1841.

（责任编辑 耿金花）