基于最优路径相似度传输矩阵的链路预测方法

李巧丽 韩华 李秋晖 曾茜

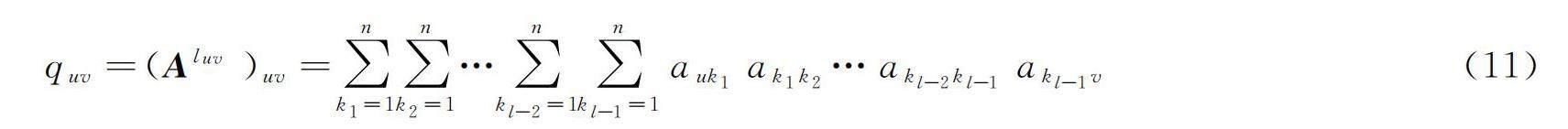
摘要：为解决现有的基于相似性的链路预测方法忽略了最优路径在节点间传递相似性的能力的问题，提出一种基于最优路径相似度传输矩阵的链路预测方法。首先，分析节点间最优路径对信息传输能力的影响，进而对节点间紧密中心性进行定义；其次，依据最优路径数和中心性构建相似度传输矩阵，综合节点间局部信息和全局属性衡量节点间相似度。最后，将所提方法与其他相似性指标，在6个真实网络上进行实证对比研究。结果表明，所提算法预测精度较高，且算法更加稳定。

关键词：复杂网络；链路预测；最优路径；相似度传输矩阵；相似性度量；中心性

中图分类号： TP393; N94文献标识码： A

收稿日期：2021-10-23；修回日期：2021-12-07

基金项目：国家自然科学基金青年科学基金（111701435）；国家自然科学基金（12071364）

第一作者：李巧丽（1991-），女，河南平舆人，硕士，主要研究方向为复杂网络动力学、链路预测。

通信作者：韩华（1975-），女，山东烟台人，博士，教授，主要研究方向为复杂性分析与评价、经济控制与决策。

Link Prediction Method Based on Optimal Path Similarity Transfer Matrix

LI Qiaoli， HAN Hua， LI Qiuhui， ZENG Xi

（Department of Science， Wuhan University of Technology， Wuhan 430070， China）

Abstract：The current similarity-based link prediction methods ignore the ability of the optimal path to transfer similarity between nodes. To solve this problem， a link prediction method based on the optimal path similarity transmission matrix is proposed. Firstly， the influence of the optimal path between nodes on the information transmission capacity is analyzed， then the tight centrality between nodes is defined; secondly， the number of optimal paths and centrality is used to construct the similarity transmission matrix， and the local information between nodes and global attributes are integrated to evaluate the similarity between nodes. Finally， the proposed method is compared with other similarity-based algorithms in six real networks. The results show that the proposed algorithm has more accurate prediction accuracy and is more stable.

Key words： complex networks; link prediction; optimal path; similarity transfer matrix; similarity measurement; centrality

0 引言

随着网络科学理论研究成果不断涌现，复杂网络已经成为分析和挖掘复杂系统的强有力工具。而链路预测作为复杂网络的重要研究方向，旨在借助网络中已知的数据信息挖掘网络中未知的连边关系^[1-2]。链路预测的研究在众多领域发挥着重要价值，从理论上来说，可以帮助我们更好地理解网络演化机制及网络动力学行为^[3]；从应用上来说，当前社交网络上的用户拓展、电信网络上的诈骗源头识别、电商网络上的客户精准营销等^[4-5]都是链路预测在现实网络中的典型应用。

目前，许多经典的链路预测算法被提出，其中基于相似性的链路预测算法应用领域最为广泛。通常包括基于节点邻居的方法（如共同邻居指标（Common Neighbors，CN）^[6]、Adamic-Adar（AA）指标^[7]、RA指标（Resource Allocation））^[3]）和基于路径的方法（如局部路径（LP）指标^[3]、Katz指标^[8]）两大类。此外，近年来学者们认为用单一的节点邻居信息来描述节点间的相似性是片面的，尝试从多个角度来刻画节点间的相似性，将节点的重要性和高阶路径信息应用到链路预测中。例如，Wu等^[9]发现共邻节点的影响力越大，对节点间相似性的贡献越小，因此，利用共邻节点的重要性排序得分对节点间的相似度进行加权，提出一种基于重要节点识别的广义链路预测方法。但该方法只利用了二阶路径信息，没有进一步挖掘更高阶的路径信息。Kumar等^[10]将传统的聚类系数概念扩展到高阶路径上^[11]，进一步提取了网络的拓扑结构信息，并利用扩展的聚类系数概念进行链路预测。文献[12]从资源传输的角度出发，试图通过惩罚共同邻居来限制信息通过共邻节点产生的“泄露”，并利用高阶路径作为判别特征，提出了基于高阶路径相似度的鏈路预测指标。

近几年，一些学者从节点间最短路径出发提出了一些新的预测链路的方法。例如，Yang等^[13]针对待预测端点对之间不存在共同邻居这一问题，结合节点间的二阶路径数和最短路径度量节点间的相似性，实验结果表明，该方法在预测无共同邻居的节点对的缺失链接方面取得了很好的效果。Ahmad等^[14]考虑到节点的共同邻居和中心性两个重要属性特征，在共同邻居的基础上，定义了节点间的紧密中心性，并将共同邻居和中心性进行线性耦合，提出了CCPA指标，有效地解决了CN指标计算结果为0或相似度分数区分不大导致的预测精度有限的问题。另外，在节点重要性研究方面，文献[15]从信息传输的角度出发，分析节点和三阶内邻居节点的相互作用，通过节点和关联节点间的最短路径长度和最短路径数度量节点间的相互影响，提出一种新的节点重要性识别方法，理论依据是最短路径数和最短路径长度在节点间影响力传输的过程中发挥着重要作用。

节点间最优路径（无权网络最优路径等价于最短路径）是网络中信息传输最直接、最有效的路径。信息总是优先选择最优路径传输，以最大化减少信息沿着路径传输过程中发生的“耗散”，使两端节点接收到更多信息量，从而两端节点更相似。实际上，节点间相似性影响与最优路径数和最优路径长度密切关联，因此，本文从信息传输的角度出发，利用最优路径作为判别特征，从节点间最优路径长度对信息传输能力的影响和节点中心性两个角度，定义节点间紧密中心性函数，再依据最优路径数和中心性构建相似度传输矩阵，综合节点对间的局部信息和全局属性刻画节点对之间的相似度，提出一种基于最优路径相似度传输矩阵的链路预测方法。该算法考虑了六阶（六度分割理论）范围内的最优路径信息，相比于CCPA算法，利用了更高阶的路径信息，简称为HOP-LP算法。

1 相关研究

1.1 问题描述

给定一个无向网络，用一个二元序对G=（V，E）表示，包含V=N个节点和E=M条边。对于网络中所有的节点，所有可能产生连边的两点集合Ω=V×V。网络G的邻接矩阵用A=（a_ij）_N×N（u，v∈V）表示，假设A中的元素a_uv=1，代表节点对（u，v）之间有连边。给定一种链路预测算法，为网络中每一对不存在的连边赋予一个分数S_xy。一般的链路预测框架是根据节点间的相似度赋予分数值，因此，将所有S_xy降序排列，排在最前面的边存在的可能性更大。

1.2 基准算法

1）共同邻居（CN）：通过节点对之间的共邻节点的个数刻画节点u和v的相似性，即

其中，Γ（u）为节点u的邻居集合，｜｜表示集合的势。

2）AA指标：是一种基于共享特征的相似性度量方法，对度大的共邻节点进行惩罚，则节点u和v的相似度定义为

其中，k_ω为节点ω的度值。

3）局部路径（LP）：为局部和全局指标在预测精度和时间复杂度之间的折衷方法，是一种半局部链路预测方法，即

其中，ε为调节参数，该指标可以扩展为

其中，n为最大阶数。随着n的增加，该指标计算复杂度会增加。

4）Katz指标：该指标实际上是一种最短路径方法，考虑了两个节点间所有的路径数，并根据路径长度的不同采取分级惩罚，则该指标表示为

其中，β为路径权重调节参数，|path^〈l〉_u，v|为节点间路径长度为l的路径数。

5）共同邻居和距离（CND）：该算法基于网络的两个重要结构特征（共同邻居和距离），对未连边的两个节点u和v的相似性用式（6）表示：

其中，CN_uv为节点u和v的共同邻居数，d_uv为节点间距离。

6）CCPA指标：Ahmad等^[14]基于节点的共同邻居和中心性两个重要属性特征，定义了两个节点间的紧密中心性，并将共同邻居和紧密中心性进行线性耦合，则该指标定义为

其中，α为调节权重参数，d_uv为节点间最短路径。

7）平均通勤时间（ACT）^[16]：基于随机游走定义的相似性指标，表示一个粒子从节点u游走到节点v所需走的平均步数，即

其中，l⁺_uv为网络的拉普拉斯矩阵中第u行第v列对应的元素值。

8）COS+指标^[17]：即余弦相似性指标，基于随机游走，在矩阵L⁺上计算两个向量间的相似度，具体表示为

其中，l⁺_uv=υ^T_uυ_y。

2 基于最優路径相似度传输矩阵的链路预测方法

复杂网络的节点间通过路径发生相互作用，路径是信息在网络中得以顺利流动的通道。文献^[18]表明最优路径长度与最优路径数在节点间信息传输的过程中发挥着重要作用。根据空间自相关理论^[19]，个体间的传输能力与距离成反比，最优路径越长，传输能力越弱。同时还与节点间的最优路径数有关，最优路径数越多，传输能力越强。假设节点x和z之间的最优路径长度l_xz和节点y和z之间的最优路径长度l_yz相等，但节点x到z之间的长度为l_xz的路径数远多于节点y到z之间的长度为l_yz的路径数，则节点x到z间的传输能力更强。

如图1所示，首先，节点8到节点2的最优路径长度（节点间距离）为2，最优路径数（二阶路径数）为1；节点4到节点2的最优路径长度为2，最优路径数为3，相比于前者，后者的最优路径数更多，故节点间传输能力更强。另一方面，节点8到节点7和节点4到7的最优路径长度都为3，但从图1中可以看出，后者的三阶最优路径数明显多于前者，因此，后者节点之间信息传输能力较强，两端节点接收到的信息量更多，从而相互连接的可能性更大。基于以上分析，下文首先基于最优路径特征定义节点间的紧密中心性，其次，给出最优路径数的代数算法，最后，将最优路径数和中心性进行线性耦合构建相似度传输矩阵，进而给出节点间相似性的度量指标。

2.1 节点间紧密中心性的量化

节点中心性即节点在网络中的相对重要性，其表征有度中心性、介数中心性和接近中心性^[18]。其中，接近中心性是指任意节点对间的平均最短路径。基于此，我们从节点间最优路径长度对信息传输能力的影响和节点中心性两个角度，给出节点对间的紧密中心性函数，表示为

其中，l_uv为节点u和v之间的最优路径长度。

2.2 最优路径数的代数算法

图1为一个无向图，它的邻接矩阵为对称矩阵。假设a_uv为A中的元素，则在图1中表示节点u到节点v之间有连边，又由于图1中不存在自环和重边，所以A中的元素只能为0或1。那么a_uv可以理解为：由u点到v点经过一条边，有a_uv种走法。同理，将其推广到A²。记B=A²，则B中的元素b_uv表示节点u出发到达节点v走两条边有b_uv种走法。

通过上述过程，记Q=A^m，Q中的元素q_uv代表的就是从u到v走m条边的路径数，但这里有重复路径，从图1可以看出，节点1到2的最优路径长度为1，但计算1到2之间的三阶路径时把长度为1的路径重复计算在内（1到2来回走三次），实际图1中并不存在1到2的长度为3的路径。为了消除重复路径，这里假设节点u和v不同，令m=l_uv，l_uv为节点u和v之间的最优路径长度，则q_uv为节点间最优路径数。

2.3 节点间相似度传输矩阵构建

针对最优路径促进节点间信息传输有效性的情况，本文基于最优路径对传输过程的影响因素分析节点间的信息传输能力。“六度分割理论”认为世界上任何两个不相识的人之间的距离不超过6个人^[20]。因此，本文在计算最优路径数时考虑六阶范围内的相似度影响，构建节点间的相似度传输能力矩阵，记为F_C：

其中，π_uv为传输能力分配参数，当节点u与v间的最优路径为六阶范围内时π_uv=1，否则为0；对角线上的1表示节点到自身的传输能力为1。F_C（u，v）代表节点u到节点v的传输能力。可以看出，节点之间的最优路径数越多，最优路径越短，则节点对间的信息传输能力越强，两端节点接收到的信息量越多，从而两端节点越相似。因此，可以由节点对间传输能力定义节点间的相似性。

定义1 基于最优路径相似度传输矩阵的链路预测方法（HOP-LP）：根据节点间最优路径对信息传输能力的影响量化节点间紧密中心性，结合节点间紧密中心性和最优路径数来度量节点间的相似性。HOP-LP的指标为

其中，式（13）中的前一项表示节点间的最优路径数（最高阶数为6），α为调节参数，用于调节最优路径数和中心性的权重，取值范围为0，1。

2.4 算法流程

首先通过设定α的取值范围，将范围内不同的α值代入算法，通过循环计算，观察不同α值对预测结果的影响，找出最佳参数α_opt，最佳参数α_opt即为算法衡量指标达到最优值时对应的参数取值（具体情况参见4.1节和4.2节）。其次，将α_opt代入HOP-LP算法中，输出节点间的相似度分数。在最佳的α_opt下，HOP-LP算法的详细步骤为：

输入：网络邻接矩阵A=（a_uv）_N×N（u，v∈V），最佳参数α_opt

输出：网络节点相似性得分矩阵

1）初始化最短距离矩阵Dis←O_N×N，节点相似性得分矩阵S←I_N×N；

2）利用A计算节点对（u，v）之间的最短路径矩阵Dis=[l_uv] //Dijkstra算法；

6）生成相應的节点相似性得分矩阵。

本文基于以下假设对算法的复杂度进行分析，即大多数网络都为稀疏的（平均度〈k〉较小）^[21]，计算最优路径数时考虑的最优路径的最大长度设为l_max=6，超过最高阶路径则认为最优路径数对刻画节点对间相似性不产生影响。HOP-LP算法的关键是计算网络中所有节点对间的最短路径矩阵Dis=[l_uv]，最短路径可以使用Dijkstra算法进行有效计算。Dijkstra算法可以采用网络的邻接列表和优先队列进行优化，优化后的时间复杂度为Ο（MlogN）。由于要为每对节点计算最短路径，故Dijkstra算法的总时间复杂度约为Ο（MNlogN）。而计算最优路径数的时间复杂度约为Ο（N/〈k〉⁶），因此，HOP-LP算法的总时间复杂度约为Ο（MNlogN）。

3 实验条件介绍

3.1 算法衡量标准

为了测试指标的预测性能，将目标网络中的连边集合E划分为训练集E^T和测试集E^P，E=E^T∪E^P，且E^T∩E^P=。其中，训练集被认为试验时已知的网络信息，测试集被认为是试验时要预测的网络信息，用于测试算法的准确度。

AUC（Area Under the Curve）指标可以理解为分别从测试集E^P和不存在的边集U-E中随机选取一条边，测试集中边的分数比不存在的边的分数更高的概率^[22]。实验时，计测试集中边的分数值高于不存在的边分数的情况为n′，两者分数相同的情况为n″，AUC指标可以表示为

其中，n为独立比较的次数，显然，随机预测下AUC≈0.5。

AUC更侧重于从整理上衡量算法的准确度，在不同的复杂网络链路预测问题中，还会有其他的要求。例如，在社交网络推荐系统中，要求算法能精准地推薦“people may you know”就能满足需求。因此，Precision衡量指标（后文简略为Pre）也应列入指标性能评价中，其关注的是前L个预测边中预测准确的比例^[23]，表示为

其中，l为预测分数值排在前L个的连边中出现在测试集E^P中的个数。在本文中，对小于1 000个节点的网络选取L=20，对大于1 000个节点的网络选取L=100。

3.2 网络数据

本文选取了6个不同的真实网络数据集：Dolphins^[24]，Polbook^[13]，Circuit^[25]，USAir^[26]，Netscience^[27]，Hamster^[28]。1）Dolphins网络：生活在新西兰神奇湾的海豚关系网络；2）Polbook网络：关于美国政治书籍的电商网络，节点表示Amazon.com线上销售的书籍，边代表同一买家频繁共同购买的书籍；3）Circuit网络：一个电子电路系统网络，其中节点是电子元件（如电容器、二极管等），连边是电线；4）USAir网络：关于美国航空运输系统的网络；5）Netscience网络：在网络科学领域发表过论文的科学家之间的合作关系网络；6）Hamster网络：有关hamsterster.com网页用户之间的朋友关系网络。上述网络数据集的拓扑特征参数如表2所列。其中，N与M分别代表节点数与边数，〈k〉为节点平均度，〈d〉为网络平均路径，C为网络集聚系数。文中选取各个网络数据集的20%作为测试集，其余的80%作为训练集。

4 实验结果及分析

为了评估本文所提算法的性能，采用AUC和Pre两个衡量指标对其进行测试和分析。实验中，每个AUC和Pre结果均为500次独立实验结果的均值。

4.1 AUC结果及分析

对于6个真实网络，首先分析了不同网络中参数α对预测结果的影响。图2展示了不同网络的AUC值随参数α的变化情况。从图2中可以观察到，不同网络中HOP-LP算法的性能受参数影响较大，从图2中的每个子图可以观察到，AUC曲线到达峰值后会呈现下降趋势，这说明最优路径数对相似性刻画的影响是不可或缺的。实验还发现，每个网络取得最佳预测精度对应的参数值并不同，α的最大值出现在Netscience网络中，为0.6，结合网络所具有的拓扑结构特征可以看出，Netscience网络的集聚系数在6个网络中最大，平均路径长度较大，这说明节点间最优路径所在阶数较低，相比于节点间最优路径长度，最优路径数对节点间相似性的影响更大；而Hamster网络的集聚系数在6个网络中最小，最优预测精度对应的参数α在6个网络中取值最小，这是由于网络的最优路径所在阶数较高，节点间的高阶最优路径数对相似度的影响较小；在Circuit网络中，AUC结果在达到最佳值后随着参数的增大有所下降，随后在最优路径数和最优路径长度达到平衡时又呈现上升趋势，说明参数对AUC的影响较为复杂。实际网络应用中，可适当调节α值，提高链路预测的准确性。

表2给出了不同网络中HOP-LP算法与其他算法的AUC值。从表2可以看出，HOP-LP算法在不同网络上的表现都是最佳的。相比于只考虑二阶路径数的CCPA算法，考虑了高阶最优路径数的HOP-LP算法在Hamster网络中预测准确率提高了约6%，这验证了考虑高阶最优路径数的HOP-LP算法能更好地利用网络结构。图3给出了9种链路预测方法在6个真实网络中的AUC值的堆积柱形图。从图3可以直观地看出HOP-LP算法每种颜色的面积几乎均匀，说明该算法能够较稳定地预测各个网络。而CN，AA，LP，Katz和ACT 5种指标每种颜色面积差别很大，表明这些指标的稳定性相对较差。纵向来看，HOP-LP算法的AUC累计值最大，其次是Katz指标，进一步验证了所提算法的有效性。

4.2 Pre结果及分析

为了进一步评估所提算法的性能，采用Pre指标对所提算法进行仿真分析。图4展示了调节参数α对Pre结果的影响，从图4可以看出，大多数网络在α较小时就能取得很好的预测性能。不同于AUC，随着参数α的增大，大部分网络的Pre值会显著下降，因此，在实际网络预测中，参数α可以在较小范围内调节，提高链路预测的准确度。

表3给出了不同算法在不同网络的Pre值。可以看出，HOP-LP算法在不同网络上的表现都是最佳的。相比于CCPA算法，尤其在Polbook网络中，预测精度提高了约32%。图5给出了9种链路预测方法在6个真实网络中的Pre值堆积柱形图。其中，USAir网络整体预测效果较好，Circuit网络的预测效果普遍较低，相比于其他算法，HOP-LP算法的Pre累计值总量第一，算法的预测结果较稳定。

5 结语

准确预测复杂网络中节点对间的相似性对于加快积极信息在网络中传播、预防电信诈骗、促进电商网络的发展具有现实意义。本文通过分析最优路径在促进节点间信息传输过程发挥的重要作用，提出一种基于最优路径相似度传输矩阵的链路预测方法。该算法分析了最优路径长度和六阶范围内最优路径数对节点相似性的贡献，定义了节点间紧密中心性函数，结合节点间局部和全局属性信息，取得了全面的相似性度量结果。在6个真实网络数据集上进行实证分析，结果验证了所提方法的可行性和稳定性。下一步将研究加权网络的特征，挖掘加权网络中的潜在连边。

参考文献：

[1]GUL H， AMIN A， ADNAN A， et al. A systematic analysis of link prediction in complex network[J]. IEEE Access， 2021， 9： 20531-20541.

[2]BRUGERE I， GALLAGHER B， BERGER-WOLF T Y. Network structure inference， a survey： motivations， methods， and applications[J]. ACM Computing Surveys， 2018， 51（2）： 1-39.

[3]ZHOU T， L? L Y， ZHANG Y C. Predicting missing links via local information[J]. European Physical Journal B， 2009， 71（4）： 623-630.

[4]CANNISTRACI C V， ALANIS-LOBATO G， RAVASI T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks[J]. Scientific Reports， 2013， 3（4）： 1613-1613.

[5]ASSOULI N， BENAHMED K， GASBAOUI B. How to predict crime informatics-inspired approach from link prediction[J]. Physica A： Statistical Mechanics and Its Applications， 2021（8）： 125-143.

[6]LORRAIN F， WHITE H C. Structural equivalence of individuals in social networks[J]. The Journal of Mathematical Sociology， 1971， 1（1）： 49-80.

[7]ADAMIC L A， ADAR E. Friends and neighbors on the Web[J]. Social Networks， 2003， 25（3）： 211-230.

[8]KATZ L. A new status index derived from sociometric index[J]. Psychometrika， 1953， 18（1）： 39-43.

[9]WU J H， SHEN J， ZHOU B， et al. General link prediction with influential node identification[J]. Physica A： Statistical Mechanics and Its Applications， 2019， 523（ 6）： 996-1007.

[10] KUMAR A， SINGH S S， SINGH K， et al. Level-2 node clustering coefficient-based link prediction[J]. Applied Intelligence， 2019， 49（7）： 2762-2779.

[11] YIN H， BENSON A R， LESKOVEC J. Higher-order clustering in networks[J]. Physical Review E， 2018， 97（5）： 052306.

[12] 顧秋阳， 吴宝， 池仁勇. 基于高阶路径相似度的复杂网络链路预测方法[J]. 通信学报， 2021， 42（7）： 61-69.

GU Q Y， WU B， CHI R Y. Link prediction method based on the similarity of high path[J]. Journal on Communications， 2021， 42（7）： 61-69.

[13] YANG J， ZHANG X D. Predicting missing links in complex networks based on common neighbors and distance[J]. Scientific Reports， 2016， 6（1）： 1-10.

[14] AHMAD I， AKHTAR M U， NOOR S， et al. Missing link prediction using common neighbor and centrality based paramete-rized algorithm[J]. Scientific Reports， 2020， 10（1）： 1-9.

[15] 胡钢， 高浩， 徐翔， 等. 基于重要度传输矩阵的复杂网络节点重要性辨识方法[J]. 电子学报， 2020， 48（12）： 2402-2408.

HU G， GAO H， XU X， et al. Importance identification method of complex network nodes based on importance transfer matrix[J]. Acta Electronica Sinica， 2020， 48（12）： 2402-2408.

[16] KLEIN D J， RANDIC M. Resistance distance[J]. Journal of Mathematical Chemistry， 1993， 12（1）： 81-95.

[17] FOUSS F， PIROTTE A， RENDERS J M， et al. Random- walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Transactions on Knowledge and Data Engineering， 2007， 19（3）： 355-369.

[18] BAO Z K， MA C， XIANG B B， et al. Identification of influential nodes in complex networks： method from spreading probability viewpoint[J]. Physica A： Statistical Mechanics and Its Applications， 2017， 468： 391-397.

[19] GRIFFITH D A， CHUN Y. Spatial autocorrelation in spatial interactions models： geographic scale and resolution implications for network resilience and vulnerability[J]. Networks and Spatial Economics， 2015， 15（2）： 337-365.

[20] 周丽娜， 李发旭， 巩云超， 等. 基于K-shell的超网络关键节点识别方法[J].复杂系统与复杂性科学， 2021， 18（3）： 15-22.

ZHOU L N， LI F X， GONG Y C， et al. Identification methods of vital nodes based on K-shell in hypernetworks[J]. Complex Systems and Complexity Science， 2021， 18（3）： 15-22.

[21] 郭世泽， 陆哲明. 复杂网络基础理论[M].北京：科学出版社，2012.

[22] KUMAR A， MISHRA S， SINGH S S， et al. Link prediction in complex networks based on significance of higher-order path index （SHOPI）[J]. Physica A： Statistical Mechanics and Its Applications， 2020， 545： 123790.

[23] ZHOU T， Lee Y L， Wang G. Experimental analyses on 2-hop-based and 3-hop-based link prediction algorithms[J]. Physica A： Statistical Mechanics and Its Applications， 2021， 564： 125532.

[24] LUSSEAU D， SCHNEIDER K， BOISSEAU O J， et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology， 2003， 54（4）： 396-405.

[25] MILO， R. ITZKOVITZ S， KASHTAN N， et al. Superfamilies of evolved and designednetworks[J]. Science， 2004， 303（5663）： 1538-1542.

[26] ZENG A， LIU W. Enhancing network robustness against malicious attacks[J]. Physical Review E， 2012， 85（6）： 066130.

[27] GUIMERA R， DANON L， DIAZ-GUILERA A， et al. Self-similar community structure in a network of human interactions[J]. Physical Review E， 2003， 68（6）： 065103.

[28] ADAMIC L A， GLANCE N. The political blogosphere and the 2004 U.S. election： divided they blog[C]// Proceedings of the 3rd International Workshop on Link Discovery， Chicago. USA， 2005： 36-43.

（責任编辑 耿金花）