基于图熵聚类的重叠社区发现算法

施欢欢　印安涛

摘要：图聚类算法是数据挖掘和复杂网络研究中的一个关键环节。基于密度、层次划分的方法已经被广泛应用于流行病学、新陈代谢和科学引文写作中。尽管上述的聚类方法适用于复杂网络的社区发现，但精度受到限制，其中一个最大的挑战是重叠社区的生成。为填补这·缺口，提出了一种利用图熵搜索局部最优的聚类方法。与传统的基于密度的种子生长式方法不同，在每一次迭代中，引入图熵来衡量图结构的模块度，并为种子的选择提供了随机选择、基于节点的度和基于节点的聚类系数3种方案。经过自下而上迭代的聚类，引入准确率和召回率等评价指标评估聚类结果的精确度，证明了算法的有效性。

关键词：图聚类算法；图熵；复杂网络；重叠社区

复杂网络在当今社会随处可见，往往蕴含着重要的信息。复杂网络规模庞大，节点连接复杂，直接对其进行研究比较困难。对复杂网络中的社区结构进行研究，已成为当下的流行趋势。社区结构经常重叠，存在同属于几个社区的节点。与此同时，许多社区结构会递归组合成一个层次结构。现存的方法忽视了社区的相互关系及其重叠，然而对于这部分的研究具有重要的实际意义。无论是寻找热门的微博话题，还是医学上对功能相关蛋白质组的寻觅，对社区结构的关系及重叠社区的深入探究都将影响巨大。

文章首先借鉴信息论中信息熵的概念，根据信息熵的公式定义节点熵和图熵的公式。图熵是节点熵的总和，作为聚类的模块度的度量，图熵越低则表明图中模块度越高。据此文章提出一种基于图熵聚类的重叠社区发现算法，把图熵作为种子生长的聚类过程中添加或删除节点的依据。实验部分，为种子的选择提供了随机选择、基于节点的度和基于节点的聚类系数3种解决方案，并对实验结果进行分析对比。

1 相关工作

很多聚类算法被运用到复杂网络的社区发现中，可以被总结为三大类：基于密度的方法、层次方法和基于划分的方法。

1.1 基于密度的方法

基于密度的方法发掘网络中内部连接密集的子图，根据对象周围的密度不断增长聚类。典型的例子是发现完全子图的最大团算法。相对密集的子图通过使用密度阀值或者结合渗透的小规模团被确定。选取种子作为初始节点，通过可替换的密度函数扩张这些种子。Mc0DE通过计算每个节点v的核心聚类系数给v设置权重，核心聚类系数是节点v和v的k个核心邻居的密度，能够放大内部连接密切的区域。算法选取权重最高的节点，通过递归地纳入不违背阀值的邻居节点扩大聚类。该方法需要预先设定阀值，这是基于密度的种子生长方法的缺陷。

1.2 层次方法

层次聚类方法创建层次以分解网络，能够帮助了解整个网络功能组织的结构，因此被广泛运用到复杂网络的分析中。自底向上的凝聚算法初始时把每个节点都看作一个独立的聚类，通过迭代合并两个最近或最相似的集合完成最终的聚类。与之相反，自顶向下的分裂算法把整个图看成一个聚类，然后递归地将单个大聚类分割成众多小聚类。凝聚算法中两个聚类的距离或相似度需要严格计算。分裂算法的挑战是找到精确的分割点，其中使用最广泛的是GN算法。

1.3 基于划分的方法

划分方法首先创建k个划分，然后利用循环定位技术将对象从一个划分移到另一个划分来帮助改善划分质量。为了达到全局最优，基于划分的方法需要穷举所有可能的分区。最常见的是k均值算法，每个聚类都用该聚类中对象的均值表示。

2 问题定义

尽管上述的聚类方法适用于复杂网络的社区发现，但精度受到限制，其中一个最大的挑战是重叠社区的生成。一个节点可能属于不同的社区，所以要求聚类方法能够分配节点到多个不同的聚类中。但一般的基于划分的方法和层次方法总是产生不相交的集合，因此只有基于密度的方法适用于挖掘重叠聚类。与传统的基于密度的方法不同，文章引入图熵来衡量图结构的模块度。把熵的概念运用到图中，可以定义每个节点的节点熵并计算整个图的图熵度量图的模块度。图熵越低表示模块度越高，因此图熵可以作为在种子生长的聚类过程中添加或删除节点的依据。

对于无向图G=（V，E），假设G是由一群聚类组成，其中一个聚类是G=（y，E）。G内部节点连接密集，G外部节点连接稀疏。对于G中任意一个节点v，v有在y内的邻居和在y外的邻居，定义v的内连接为从v到V内邻居节点的边数，定义v的外连接为从v到V外邻居节点的边数。定义p_i（D为节点v的内连接率，公式表达为：（1）

其中|N（v）|为节点v的所有邻居节点数，n为节点v的内连接数。则v的外连接率p₀（v）公式表达为：

p₀（v）=1-p_i（v） （2）

对于节点v，它的熵值取决于它的内连接和外连接的分布概率，参考信息熵，定义v的节点熵公式为：

e（v）=-p_i（v）long₂p_i（v）-p₀（v）long₂p₀（v） （3）

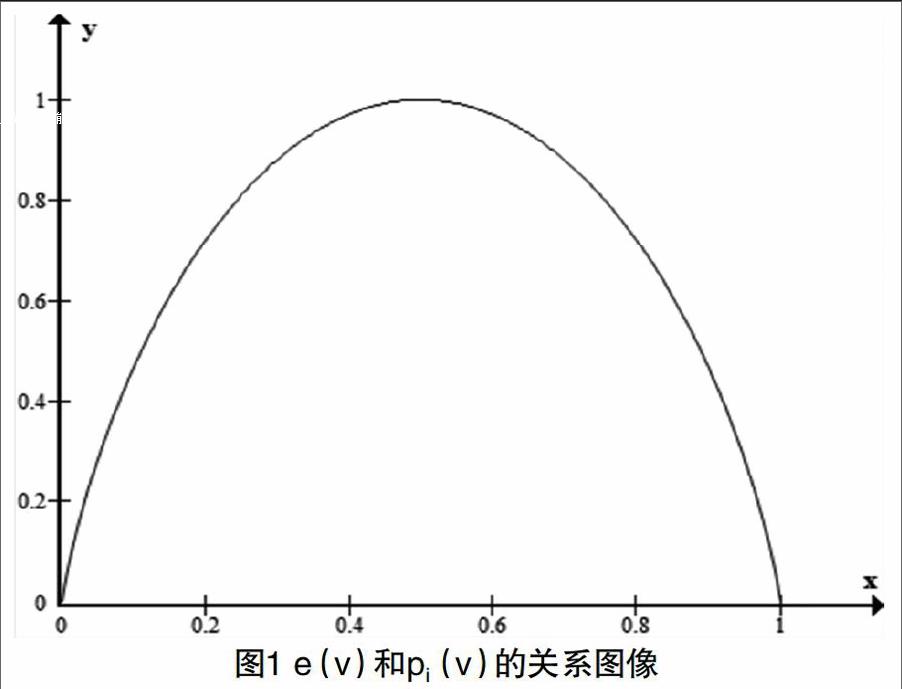
其中0≤p_i（v）≤1，因此可以得到e（v）和p_i（v）的关系图像如图1所示。

根据图1，当节点v的所有邻居节点全部在聚类内部或全部在聚类外部时，节点v的熵值最小，即e（v）=0；当节点v的邻居节点均匀分布在聚类内部和聚类外部时，节点v的熵值最大，即e（v）=1。

图熵定义为图G=（V，E）中所有节点的节点熵之和，公式表达为（4）

图熵是基于密度的定义，可以有效衡量聚类质量。图熵越低表明图中节点内连接率越高，外连接率越低。通过最小化图熵的值不断增加或删除节点后得到的聚类就是一个社区。

3 算法

基于图熵的聚类算法是一种种子生长型算法，通过反复最小化图熵的值发掘局部最优聚类。如图2所示，圆圈区域为聚类内部，加入节点d后，熵值减少，因此节点d被纳入聚类；加入节点e后，熵值增加，节点e被拒绝纳入聚类。

初始时单个种子是一个聚类，然后通过最小化图熵的方式生长成最终聚类。算法详细伪代码如下：

算法：SeedGrowthEntropy

输入：图G=（V，E）

输出：聚类集合列表（包括重叠聚类）。

Step 1：图中的每一个节点都是候选种子。从候选种子中选取一部分节点作为种子节点并存入种子集中。

Step 2：从种子集中选取一个种子，加入它的所有邻居节点形成一个聚类。

Step 3：迭代移除聚类内的邻居节点如果移除能降低熵值。

Step 4：迭代添加当前聚类外的边界节点如果添加能降低熵值。

Step 5：输出具有最小图熵值的聚类并从种子集中删除该种子。

Step 6：重复step2、step3、step4和step5直到种子集中没有种子剩余。

熵值聚类的主要思想是通过模块化函数（图熵）搜索局部最优社区。由于每次聚类结果输出后都不会删除聚类节点而是删除种子集中的种子节点，确保了每个种子的生长都是从所有节点中进行选择的。一个节点可能在多个种子生长时被选中，因此该算法能够输出重叠聚类，对应的就是重叠社区。种子的选择就变得比较重要，既能让选择的种子的聚类结果覆盖大部分网络，又能提高算法的运行效率。根据复杂网络中无标度的特征，网络中小部分节点连接稠密，大部分节点连接稀疏。如果选取的种子是连接稀疏的节点，这样的聚类没有意义。因此种子的选择可以基于节点的度或者节点的聚类系数。度越大或者聚类系数越大的节点更有机会是一个好种子。

4 评估方法和实验结果

文章进行了多组实验对算法进行评估，种子的选择分为随机选择、基于节点的度和基于节点的聚类系数3种方式。算法由Java语言实现。

4.1 实验数据

文章仅考虑无向图数据集，使用亚马逊合买产品网络和它的地面实况社区。数据集来自于斯坦福大学提供的复杂网络分析平台SNAP（Stanford Network Analysis Project）中的Stanford Large Network Dataset Collection部分（http：//snap.stanford.edu/data/index.html）。如果商品i经常和商品j一起被买，那么网络中i和j之间就有一条无向边相连，很多件商品和边共同构成复杂网络。亚马逊提供的每个商品决定了每个地面实况社区。地面实况是指“ground-truth”，是搜集到的准确客观的数据，用于验证实验结果的准确性。认为产品类别中每个连接的部分是一个独立的ground-truth社区，移除掉节点数少于3的社区后，一共有75491个真实社区。数据详细情况如表1所示。

4.2 评价标准

falsef-measure直接比较每个输出聚类和网络中的真实社区，量化输出聚类和每个功能模块的匹配度，能够评估聚类结果的精确度。对于基于图熵聚类算法输出的一个聚类c.和网络中一个真实社区p_i，召回率（recall）也叫作真阳性或敏感度，定义为c_i和p_i公共节点数占p_i点数的比率，公式表达为：

recall=|c_i∩p_i|/|p_i| （5）

准确度（precision）也叫作阳性预测值，定义为c_i和p_i公共节点数占c_i节点数的比率，公式表达为：

precision=|c_i∩p_i|/|c_i| （6）

f-measure的值f-recall为recall和precision的调和平均数，公式表达为：（7）

关于f-score，对每个输出聚类c从真实社区列表中搜索最匹配的社区p_i进行计算。然后求出所有最佳匹配的f-score的平均值作为聚类算法的精确度评价标准。

4.3 实验结果和分析

一种情况下种子的选择是随机的，但是潜在的聚类核心更适合做种子，因此考虑两种不同的基于节点连通性的方法来寻找网络中的局部核心。第一种方法基于节点的度，第二个方法基于节点的聚类系数。在种子选择中，分配具有较高度或者较高聚类系数的节点较高的优先级。文章对以上3种情况分别进行实验。

以基于度的方法为例，实验结果如图3所示，聚类结果保存在.txt文件中，每一行是一个聚类。一共有33178行，表明算法生成了33178个社区（剔除节点数少于3个的社区）。社区的大小和个数分布如图4所示（横轴表示社区大小，纵轴表示社区个数）。可以看出，小规模社区分布众多，随着社区规模的增长，社区个数急速下降，最大的社区规模为324。

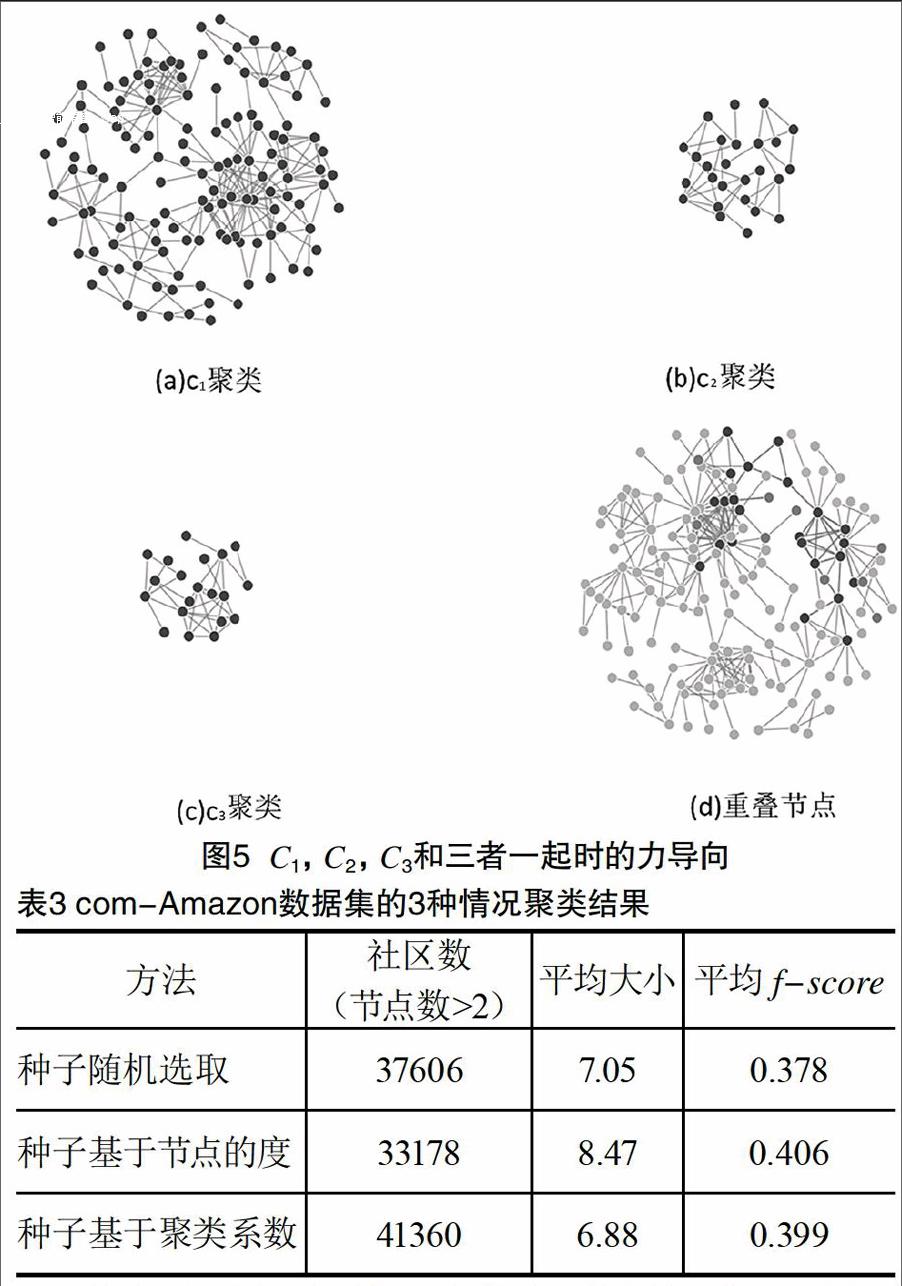
为了验证重叠社区，以输出结果中的c₁，c₂和c₃3个聚类为例，3个聚类规模大小不一，节点信息见表2，其中数字串为商品编号。图5中（a），（b），（c）分别为c₁，c₂和c₃3个聚类各自的力导向图，（d）为3个聚类一起时的力导向图，（d）中深色节点为重叠节点，表明算法确实发现了重叠社区。根据3种情况的实验结果，得到如表3所示的结果。

从表3中看出，和随机选取的种子集相比，基于节点的度的种子集得到的社区数量更少但规模更大，而基于聚类系数的种子集得到的社区数量更大但规模更小。度高的节点由于接入更多的间接邻居而影响很大一块区域，所以社区规模大一些；而聚类系数高的节点限制了接入的邻居个数导致社区规模小一些。宏观看3个方均f-score差不多，基于度的结果更好一些，基于聚类系数的略差些，随机选取排在最后，都维持在0.4左右，考虑到社区的基数比较大，这个结果足以表明基于图熵的聚类方法具有良好的精确度。

5 结语

文章提出一种基于图熵聚类的重叠社区发现算法，旨在发现给定复杂网络中的绝大部分社区，包括重叠社区。算法引入图熵的概念来衡量子图的模块化程度，通过最小化图熵搜索局部最优的方法自底向上发掘所有社区，并且能够发现重叠社区。文章首先介绍了被运用到复杂网络的社区发现的聚类算法，主要分为三大类：基于密度的方法、层次方法和基于划分的方法。然后介绍了节点熵和图熵的概念。最后详细描述了基于图熵聚类的算法，并为种子的选择提供了随机选择、基于节点的度和基于节点的聚类系数3种解决方案。实验结果表明提出的算法有很好的效率，可以有效解决提出的问题，具有重要的实际意义。