基于复杂网络的新冠病毒群体免疫数值仿真

王佳亮 李海滨 李海燕

摘要：鉴于构建流行病动力学模型、探索流行病传播规律对疫情防控具有十分重要的理论意义和实际应用价值，在已有的均匀混合模型基础上，针对个体接触关系异质化越发明显，且每个个体都处在不同的接触关系中，建立了兼顾个体状态与接触追踪的动态小世界网络模型。模拟了新冠病毒在社会中的传播过程。通过对比仿真结果，说明了所建模型的合理性。在此基础上，仿真计算了网络拓扑结构与接种免疫人数占比共同作用下对新冠病毒传播的影响，分析得到群体免疫临界值。说明所建传播模型合理，接种疫苗实现群体免疫可行。

关键词：小世界网络；动力学建模；新冠病毒；群体免疫

中图分类号： TP391.9文献标识码： A

收稿日期：2021-09-06；修回日期：2021-12-31

基金项目：国家自然科学基金（11962021）

第一作者：王佳亮（1996-），男，内蒙古赤峰人，硕士研究生，主要研究方向为系统动力学建模与仿真。

通信作者：李海滨（1973-），男，内蒙古呼和浩特人，博士，教授，主要研究方向为结构不确定性分析与量化、神经网络计算、六维力传感器设计。

李海燕（1980-），女，内蒙古呼和浩特人，本科，副主任护师，主要研究方向为内分泌疾病与糖足的临床护理。

Numerical Simulation of the COVID-19 Herd Immunity Based on Complex Network Modeling

WANG Jialiang^1a， LI Haibin¹， LI Haiyan²

（1. a. College of Sciences; b. Engineering Training Center of Inner Mongolia University of Technology， Hohhot 010051， China; 2. Department of Endocrinology the First Affiliated Hospital of Inner Mongolia Medical University， Hohhot 010010， China）

Abstract：Constructing an epidemic dynamic model and exploring the spreading law of epidemic have very important theoretical significance for epidemic prevention and control. Based on the existing homogeneous mixing model， in view of the increasingly obvious heterogeneity of individual contact relationships， and each individual is in a different contact relationship， a dynamic small-world network model that takes into account individual status. Contact tracking has been established to simulate the spread of the COVID-19 in society. By comparing the simulation results， the rationality of the built model is explained. On this basis， the simulation calculated the impact of the network topology and the proportion of vaccinated people on the spread of the COVID-19， analyzed the critical value of herd immunity. The established propagation model is reasonable， and feasible to achieve herd immunization by vaccination.

Key words： small world network; dynamic modeling; COVID-19; herd immunity

0 引言

自從人类社会诞生以后，传染病一直是困扰人类的难题之一，从早期的黑死病、天花、麻疹，到近期的埃博拉（EBOV）、寨卡病毒（Zika Virus）和新型冠状病毒（COVID-19）^[1]。随着航空、高铁等交通网络的飞速发展，便捷的交通为人类出行带来方便，同时也为流行病迅速传播提供了条件。建立流行病动力学模型、探索病毒传播规律、提供有效预防措施是疫情防控的重要研究内容。

经典的均匀混合动力学模型由Kermack和McKendrick于1926年提出，随后基于此工作，出现了SEIR（Susceptible Exposed Infected Removed）、SEIQR（Susceptible Exposed Infected Quarantined Removed）等一系列扩展模型用来研究流行病传播，并取得了诸多重要结论和成果。针对新冠疫情，Fang等^[2]应用SEIR模型进行仿真模拟和数据拟合，预测了武汉疫情确诊病例数的峰值，仿真结果表明所建模型具有较高的拟合精度。范如国等^[3]利用SEIR模型，模拟了5，7，10天3种不同潜伏期下的武汉疫情，预计此次疫情拐点在第71，74，78天出现。钟南山院士团队^[4]利用优化的SEIR模型和人工智能方法预测国内疫情将在2月底达到高峰，4月底趋于平缓。如果封城等管控措施推迟5天实施，中国国内的疫情规模将扩大3倍。Gu等^[5]利用SEIR模型研究了COVID-19的传播速度、空间范围和动力学机制，并对国内疫情的扩散趋势进行了预测。Mwalili等^[6]利用改进的SEIR模型，探索了新冠疫情在不采取防控措施下的蔓延情况，结果表明，若不加以防控，新冠疫情将在世界范围内持续扩散，从而产生毁灭性影响。的确经典的均匀混合动力学模型已经为流行病的防控做出了应有的贡献，但是在个体间接触关系异质化越来越明显的情况下，均匀混合动力学模型已经无法描述目标人群内部复杂的动力学性质。基于网络建立的流行病动力学模型能够很好反映个体间接触关系，从而出现了利用复杂网络研究流行病传播的动力学模型。杨洪勇等^[7]利用小世界网络模型模拟了禽流感病毒的传播过程，通过与实际数据对比来说明所构建模型的有效性。程静等^[8]用小世界网络模型对埃博拉病毒的传播情况进行了仿真，仿真结果与实际报道的传播情况相符。刘汉卿等^[9]利用小世界网络模型研究了COVID-19在其网络中的传播规律以及通过控制节点行为对其传播的影响，数据仿真结果验证了模型的适用性。上述工作表明基于小世界网络的流行病动力学模型不仅能描述个体状态转化关系，还能够描述个体间的有效接触关系。因此，本文尝试采用小世界网络构建流行病传播模型，以更好模拟新冠病毒在现实中的接触传播过程。

目前，中国的防控措施已从积极发现并隔离病例、追踪隔离密切接触者、控制人群流动，发展到针对局部疫情暴发迅速采取多轮大规模人群病毒核酸检测，形成了行之有效的防控策略^[10]。然而，非药物干预措施下的疫情防控仍然面临着外来输入的风险，经过科研人员的不懈努力，中国已经成功研制出针对新型冠状病毒的疫苗，中国国家药品监督管理局于2020年12月30日批准了国药集团中国生物北京生物制品研究所新冠病毒灭活疫苗的注册申请^[11]。在中国新冠疫情防控进入疫苗时代，通过构建群体免疫屏障来战胜新冠病毒成为可能。所谓群体免疫，就是在人群中让大多数人对某种传染病产生免疫力，在社会层面形成一道保护屏障，当一个或者多个传染病患者进入这样的人群时，也不会出现传染病暴发的情况^[12]。那么，接种疫苗人群占比多少能够达到群体免疫效果是一个很有研究意义的问题。针对这一问题，吴丹等^[13]根据新冠病毒的基本再生数R0=1.6～6.5，通过基本再生数与群体免疫临界值的关系式计算得到群体免疫临界值为38%～85%。目前给出的群体免疫临界值都是根据基本再生数通过关系式计算得到，属于经验估计，缺乏必要的实验或仿真验证。因此，本文将在动态小世界网络中仿真计算免疫个体占比对新冠病毒传播的影响，根据仿真结果给出群体免疫临界值。

1 动态小世界网络上的流行病动力学建模与仿真

在动态小世界网络中研究新冠病毒扩散动力学过程，包括：在具有复杂拓扑结构的网络中研究新冠病毒的传播，以及由于新冠病毒传播对网络中不同状态节点的影响。不仅需要考虑网络的拓扑结构，还需要确定新冠病毒的传播模式。本节将用小世界网络模型模拟新冠病毒传播过程，并与已有均匀混合模型做对比，来说明所建模型的合理性。

1.1 小世界网络上的新冠病毒传播模型

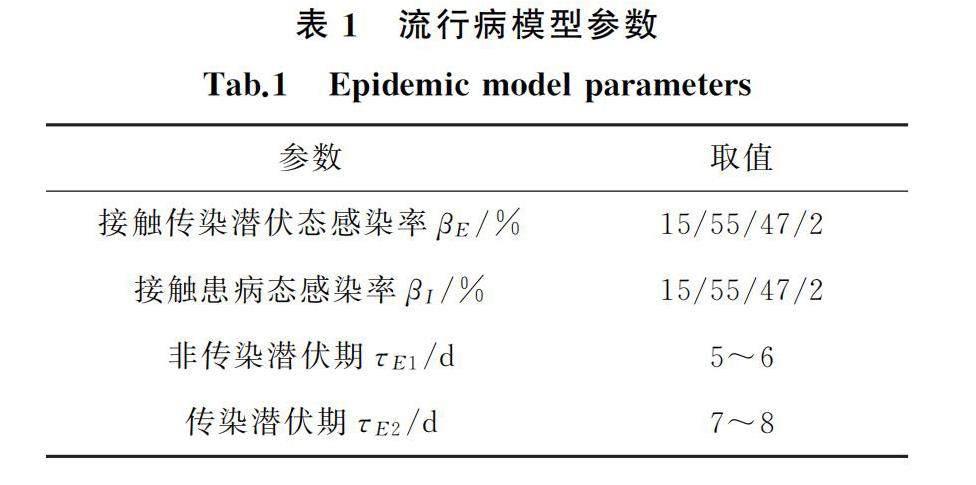
小世界网络模型最早由Watts和Strogatz提出，具有N个节点的小世界网络模型构造规则为^[14]：1）首先将N个节点排列成一个圆并顺时针按序编号，每个节点与其左右最近邻的各K/2个节点连线，生成一个具有N·K/2条边的最近邻规则网络；2）将步骤1）生成的规则网络中的每一条边以概率p进行断线重连处理，重连过程中，保证网络没有重复边和自连接的情况。当p=0时，对应规则网络；当p=1时，对应随机网络；当0

流行病在传播过程中，个体的状态可分为易感态S、潜伏态E、有症状的患病态I、无症状的患病态A、隔离态Q、治愈态R和死亡态D等几种基本状态。其中，除了易感态S和有症状的患病态I是必选之外，其它状态要根据实际需要加以选择^[15]。根据新冠病毒传播特性，本文将目标人群中的个体状态分为5类：易感态S（未患病但可以被感染）；非传染潜伏态E1（無症状患病态但不具有传染性）；传染潜伏态E2（无症状患病态且具有传染性）；患病态I（有症状患病态且具有传染性）；隔离态Q（被隔离的有症状患病态）。根据新冠病毒传播规律，易感态个体被接触感染后变为潜伏态，文献[16]表明，潜伏态个体在潜伏期初期不具有传染性，到了潜伏期后期开始具有传染性。因此，将潜伏态个体分为非传染潜伏态和传染潜伏态2个相互独立的状态。潜伏态个体经过潜伏期后变为患病态，之后以一定概率被隔离。至此，完成了对任一易感态个体从感染到隔离全过程的运动轨迹跟踪描述。所以，本文确定网络中节点状态转化过程如下：当网络中的节点处于易感态时，与其相连的每一个传染潜伏态节点以概率β_E对其进行感染，与其相连的每一个患病态节点以概率β_I对其进行感染，同时需要判断该节点是否被感染为非传染潜伏态；当网络中的节点处于非传染潜伏态时，该节点经过非传染潜伏期τ_E1后转化为传染潜伏态；当网络中的节点处于传染潜伏态时，该节点经过传染潜伏期τ_E2后转化为患病态；当网络中的节点处于患病态时，该节点将以概率γ_Q被隔离转化为隔离态。上述节点状态转化过程如图1所示，对应动力学方程如式（1）所示。

综合上述分析，将小世界网络上的新冠病毒传播过程总结为：1）初始化，生成一个具有N·K/2条边的最近邻规则网络。2）小世界网络，将规则网络中的每一条边以概率p进行断线重连处理，重连过程中，保证网络没有重复边和自连接的情况。3）引入传染源，在网络中随机选取比例为E0的非传染潜伏态个体作为初始传染源，其余为易感态个体。4）开始传染，网络拓扑结构变化与节点状态转化同步进行，每同步进行一次为一个迭代步，周期为1 d。5）记录数据，统计每一个迭代步所有节点的状态，在观测时间点上统计数据并作图。

1.2 小世界网络上新冠病毒的传播仿真

本节将通过与文献[17]中的时滞均匀混合模型仿真对比来验证所构建模型的合理性。在仿真之前首先要确定模型参数。

待定的模型参数有β_E，β_I，τ_E1，τ_E2，γ_Q。其中，接触感染率β_E，β_I和潜伏期时间常数τ_E1，τ_E2等参数反映的是病毒传播特性。文献[15]根据武汉某医院新冠患者接触治疗情况给出了一次接触感染率β_E，β_I；文献[18]给出了新冠病毒潜伏期参数估计的研究报道，潜伏期中位数为5.5 d，95%患者的潜伏期不超过13 d。据此本文设定新冠病毒的潜伏期为12～13 d，大致分为两个阶段，即非传染潜伏期τ_E1为5～6 d、传染潜伏期τ_E2为7～8 d。将上述各参数列于表1。隔离率γ_Q的设定取决于对疫情防控的响应速度。

在上述参数条件下，分别利用小世界网络模型和文献[17]中的时滞均匀混合模型进行疫情动力学仿真。取网络节点总数N=5 000，每个节点初始拥有的邻居节点个数K=28，断线重连率p=0.05，非传染潜伏态个体占比E0=0.01，其他参数见表1，以180 d为观测终点进行仿真。在上述各态不考虑隔离措施情况下，图2中的“—”模拟了新冠疫情在动态小世界网络中传播的全过程；图2中的“○”为同参数条件下文献[17]中的时滞均匀混合动力学模型仿真所得结果。

对比图2所得结果可以看到，两种方法在疫情传播过程中各态节点变化趋势高度吻合，可以说明本文所建模型的合理性。由于文献[17]中的均匀混合传播模型是以时滞微分方程形式描述的，模型给定初始条件后，应用MATLAB中的“dde23”可以求出确定的解；且均匀混合传播模型对应“全连通网络”，表示为任意一个患病态个体可以把病毒传染给网络中任意一个易感态个体。本文所构建的动态小世界网络传播模型，既考虑了新冠病毒传播过程中的随机性，又根据网络拓扑结构来说明实际的患病态个体只把病毒传染给了所接触的有限个体，从而造成了仿真结果的差异。基于网络建立的传播模型，既涵盖了病毒的传播特性，又包含了自身结构的特性，可以使人们对新冠病毒接触传播的过程认识更加清晰。

2 基于网络的群体免疫数值仿真

以最小的代价去控制流行病的传播，将流行病扩散造成的影响和损失降到最低，可以通过对人群中大部分人进行免疫来实现，这样不仅接种疫苗的免疫者能够得到保护，全人群也可能获得保护。因此，本节将在动态小世界网络中讨论免疫个体占比对新冠病毒传播的影响。主要包括两方面工作：1）仿真对比有、无免疫个体两种情况下，新冠病毒在动态小世界网络中的传播过程，通过仿真结果来说明，由于免疫个体的存在对病毒传播造成的影响。2）在网络拓扑结构与初始免疫人数占比共同作用下，在不同观测节点上仿真计算了新冠病毒传播的最终感染人数占比；根据感染人数占比计算有效再生系数，分析给出了群体免疫临界值。

首先通过仿真来说明免疫个体的存在对新冠病毒传播的影响。取网络节点总数N=5 000，每个节点初始拥有的邻居节点个数K=24，断线重连率p=0.05，非传染潜伏态个体占比E0=0.01，初始免疫个体占比R=0.2，其他参数见表1，以90 d为观测节点进行仿真。图3、图4分别模拟了有、无免疫个体情况下新冠病毒的传播过程。

分析图3与图4所得结果，在90 d观测节点上，无免疫个体时最终感染人数占比约为51.68%，有免疫个体时最终感染人数占比约为17.66%，其中感染人数占比为非传染潜伏态、传染潜伏态、患病态个体占比的总和。通过仿真结果可以看出，免疫个体的存在能够大幅减少病毒扩散。

在网络中讨论接种免疫人数占比对病毒传播的影响，需要考虑网络的拓扑结构，以及初始免疫人数的占比。假设表征网络拓扑结构的参数用平均路径长度L来描述，平均路径长度是指网络中连接任意两个节点所要经过的最少连边个数的平均值^[19]。由于图3所得结果仅选择了一组参数，下面将对模型参数取不同的值分别进行仿真计算，以探索表征网络拓扑结构的参数L与初始免疫人数占比R共同作用下，对网络中新冠病毒传播最终感染人数G占比的影响。取网络节点总数N=5 000，非传染潜伏态个体占比E0=0.01保持不变，为了得到不同观测节点上感染人数G的占比，将在随机变量L和R组成的各离散点上，分别以30 d，60 d，90 d为观测节点进行仿真计算，所得结果如图5所示。

分析图5所得结果，当网络的平均路径长度L较小时，病毒在网络中的传播速度较快；随着免疫人数占比的逐渐增加，病毒在网络中的传播速度减慢，最终感染人数占比减少。下面将根据感染人数占比计算有效再生系数，分析给出不同观测节点上的群体免疫临界值。

通过式（2）^[20]：

计算有效再生系数，其中，total（t）为第t天的感染人数占比（见图5），t为传播天数，取值为30，60，90；n为初始的感染人数占比，取值为0.01；k为有效再生系数；将图5中所得的每种情况的total（t）分别对有效再生系数k进行计算，所得结果如图6所示。

综合分析图5、图6所得结果，在30 d观测节点上，当免疫人数占比达到35%左右时，感染人数占比最多为1.88%，有效再生系数k=0.468 08，小于0.5，可以认为达到群体免疫效果。在60 d观测节点上，当免疫人数占比达到65%左右时，感染人数占比最多为1.81%，有效再生系数k=0.447 51，小于0.5，可以认为达到群体免疫效果。在90 d观测节点上，当免疫人数占比达到70%左右时，感染人数占比最多为1.84%，有效再生系数k=0.456 52，小于0.5，可以认为达到群体免疫效果。

3 总结

针对流行病动力学建模，本文建立了兼顾个体状态与接触追踪的动态小世界网络上的新冠病毒传播模型，与均匀混合动力学模型相比，复杂网络上的新冠病毒傳播模型能够更好地反映个体接触的传染情况，对病毒传播过程的追踪更容易。针对疫情防控策略的群体免疫，首先仿真计算了有、无免疫个体对网络中新冠病毒传播的影响。仿真结果表明，免疫个体的存在能够大幅减少病毒扩散。之后对模型参数取不同的值进行仿真计算，定量探索了初始免疫人数占比与网络拓扑结构共同作用对新冠病毒传播的影响。根据感染人数占比通过式（2）计算有效再生系数，综合分析得到30 d，60 d，90 d观测节点上的群体免疫临界值分别为35%，65%，70%，即当初始免疫人数占比分别达到35%，65%，70%时，疫情在网络中传播30 d，60 d，90 d也不会出现暴发的情况。随着观测时间向后推移，感染人数占比呈明显上升趋势，可知疫情长期防控比短期防控难度更大，但是随着疫苗的优化与大规模接种，群体免疫屏障会越来越坚固，人类终将战胜新冠病毒。

参考文献：

[1]SARKAR A， LIU G， JIN Y， et al. Public health preparedness and responses to the coronavirus disease 2019（COVID-19） pandemic in South Asia： a situation and policy analysis[J]. Glob Health J， 2020， 4（4）： 121-132.

[2]FANG Y Q， NIE Y T， Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions： a data-driven analysis[J]. Journal of medical virology， 2020， 92（6）： 645-659.

[3]范如国， 王奕博， 罗明， 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析[J]. 电子科技大学学报， 2020， 49（3）： 369-374.

FAN R G， WANG Y B， LUO M， et al. SEIR-based COVID-19 transmission model and inflection point prediction analysis[J]. Journal of University of Electronic Science and Technology of China， 2020， 49（3）： 369-374.

[4]YANG Z， ZENG Z， WANG K， et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions[J]. Journal of Thoracic Disease， 2020， 12（3）： 165-174.

[5]GU B R. Forecast and analysis of COVID-19 epidemic based on improved SEIR model[J]. Journal of Physics：Conference Series， 2021， 1802（4）： 042050.

[6]MWALILI S， KIMATHI M， OJIAMBO V， et al. SEIR model for COVID-19 dynamics incorporating the environment and social distancing[J]. BMC Research Notes， 2020， 13（1）： 1-5.

[7]杨洪勇， 张嗣瀛. 基于复杂网络的禽流感病毒传播[J]. 系统仿真学报， 2008， 20（18）： 51-55.

YANG H Y， ZHANG S Y. Viruses epidemics of avian influenza based on complex networks[J]. Journal of System Simulation， 2008， 20（18）： 51-55.

[8]程静， 黄青， 谢铭杰， 等. 小世界网络中埃博拉病毒传播的研究[J]. 生物医学工程学进展， 2015， 36（2）： 91-94. CHENG J， HUANG Q， XIE M J， et al. Study on the transmission of ebola virus in small world network[J]. Advances in Biomedical Engineering， 2015， 36（2）： 91-94.

[9]刘汉卿， 康晓东， 高万春， 等. 基于多模型的COVID-19傳播研究[J]. 计算机科学， 2021， 48（6）： 196-202.

LIU H Q， KANG X D， GAO W C， et al. Research on propagation of COVID-19 based on multiple models[J]. Computer Science， 2021， 48（6）： 196-202.

[10] LI Z， CHEN Q， FENG L， et al. Active case finding with case management： the key to tackling the COVID-19 pandemic[J]. The Lancet， 2020， 396（10243）： 63-70.

[11] 国药集团. 国药集团中国生物新冠灭活疫苗获批附条件上市[EB/OL]. [2021-03-02]. http：//www.sinopharm.com/s/1223-4126-38840.html.

SINOPHARM. Sinopharm China biotech covid-19 inactivated vaccine approved for conditional listing[EB/OL]. [2021-03-02]. http：//www.sinopharm.com/s/1223-4126-38840.html.

[12] FINE P， EAMES K， HEYMANND D L. "Herd immunity" ： a rough guide[J]. Clinical Infectious Diseases， 2011， 52（7）： 911-916.

[13] 吴丹， 郑徽， 李艺星， 等. 群体免疫及其对传染病防控的意义[J]. 中国疫苗和免疫， 2020， 26（4）： 123-127.

WU D， ZHENG H， LI Y X， et al. Herd immunity and its importance in infectious disease prevention and control[J]. Chinese Journal of Vaccines and Immunization， 2020， 26（4）： 123-127.

[14] WATTS D J， STROGATZ S H. Collective dynamics of small-world networks[J]. Nature， 1998， 393（6684）： 440-442.

[15] 李海滨. 基于社会分工的流行病动力学建模与仿真研究[J]. 系统仿真学报， 2020， 32（5）： 745-758.

LI H B. Modeling and simulation on dynamics of epidemic disease based on social division of labor[J]. Journal of System Simulation， 2020， 32（5）： 745-758.

[16] XI H， ERIC H， LAU Y， et al. Temporal dynamics in viral shedding and transmissibility of COVID-19[J]. Nature Medicine， 2020， 26（5）： 672-675.

[17] 李海滨， 王佳亮， 李海燕. 新冠后疫情时代复学风险评估的不确定性量化分析[J]. 系统仿真学报， 2021， 33（1）： 13-23.

LI H B， WANG J L， LI H Y.Uncertainty quantitative analysis in risk assessment of returning to school in the post-COVID-19 era[J]. Journal of System Simulation， 2021， 33（1）： 13-23.

[18] 邱明， 悦胡涛， 崔恒建. 双区间删失下新冠病毒肺炎潜伏期分布的参数估计[J]. 应用数学学报， 2020， 43（2）： 200-210.

QIU M， YUE H T， CUI H J. Parameter estimation of incubation period distribution of new coronavirus pneumonia under double interval censoring[J]. Journal of Applied Mathematics， 2020， 43（2）： 200-210.

[19] 汪小帆. 復杂网络理论及其应用[M]. 北京：清华大学出版社， 2006.

[20] 王志心， 刘治， 刘兆军. 基于机器学习的新型冠状病毒（COVID-19）疫情分析及预测[J]. 生物医学工程研究， 2020， 39（1）： 1-5.

WANG Z X， LIU Z， LIU Z J. COVID-19 analysis and forecast based on machine learning[J]. Journal of Biomedical Engineering Research， 2020， 39（1）： 1-5.

（责任编辑 李 进）