考虑时滞的真假信息竞争扩散仿真研究

孙青松 胡海波 程树林

摘要：考虑到虚假信息要先于真实信息扩散且二者存在于同一个社会网络中的现象，研究了真假信息竞争扩散模型，分析比较了各种概率、真实信息初始扩散时间和扩散节点数量的影响。结果发现，采取措施降低节点扩散虚假信息的可能性可以减少虚假信息扩散范围，此外，仅当真实信息延迟扩散时间较短时，可通过增加节点扩散真实信息的可能性、增加扩散真实信息节点的数量或选择度较大的节点来扩散真实信息的方式来减少虚假信息扩散范围，并增加了真实信息覆盖面。

关键词：时滞；真实信息；虚假信息；竞争扩散

中图分类号： G206.3文献标识码： A

收稿日期：2021-10-26；修回日期：2021-12-06

基金项目：国家自然科学基金面上项目（61973121）；安徽省高等学校自然科学研究重点项目（KJ2018A0362）；安徽省自然科学基金研究项目（2008085MF193）

第一作者：孙青松（1982-），男，安徽怀宁人，博士，讲师，主要研究方向为复杂网络，信息扩散。

通信作者：胡海波（1980-），男，山东莱西人，博士，副教授，主要研究方向为复杂网络。

A Simulation Study of Competitive Diffusion of Real and Fake Information with Time-delaying

SUN Qingsong^{1， 2}， HU Haibo²， CHENG Shulin¹

（1.School of Computer and Information， Anqing Normal University， Anqing 246133， China； 2.School of Business， East China University of Science and Technology， Shanghai 200237， China）

Abstract：Considering the phenomenon that false information is diffused before real information in social networks， an information competition diffusion model is studied and the effects of different probabilities， the initial diffusion time of real information and the number of real information spreader nodes are analyzed and compared. It is found that reduing the probability of unknown nodes to diffuse false information can reduce the diffusion scope of false information. In addition， only when the delay diffusion time of real information is short， can the diffusion scope of false information be reduced and the coverage of real information be increased by increasing the probability of nodes to diffuse real information， increasing the initial number of real information spreader nodes and selecting nodes with greater degree to diffuse real information.

Key words： time-delaying; real information; fake information; competitive diffusion

0 引言

互聯网的广泛使用使得在线社会网络上各类信息不断传播扩散，社会网络已成为人们获取或传播信息的重要渠道。2020年，互联网在防控新冠肺炎疫情方面发挥了巨大作用，人们在手机网络上就可以及时了解疫情的动态消息。同时，社会网络中也常常有一些虚假信息在传播扩散，造成不利的影响。

针对社会网络中负面信息的扩散，部分研究从反驳谣言的角度出发，如Zhu等^[1]研究了辟谣机制的时滞效应对网络谣言传播的影响。朱霖河等^[2]研究了辟谣机制和时滞效应对谣言传播的影响，辟谣机制通过一个线性参数来描述，不是通过在网络中增加辟谣节点来研究。Huang等^[3]建立了一个双层网络来模拟传染病传播和信息竞争扩散之间的相互作用，结果表明，知识扩散对谣言具有一定的影响，社会网络越密集越能抑制谣言扩散。Jiang等^[4]提出了一个谣言传播-揭穿模型，将模拟与真实数据进行比较并进行验证。Ma等^[5]考虑了积极和消极两方面因素对谣言传播进行研究，结果表明减少正面强化因素或增加负面强化因素能有效抑制谣言的传播，这与一般的认识有所区别，但选择度较大和权重较大的节点能够较好地抑制谣言传播。Huo等^[6]对科学知识扩散和谣言传播的交互过程进行研究，结果发现科学知识扩散率和较低的谣言传播率对阻止谣言传播有明显影响。张菊平等^[7]考虑到在谣言传播过程中会出现真实信息传播者，在该模型中仅有一类免疫节点，未对知道虚假信息的节点和后期会成为相信真实信息的节点进行区分，也未考虑谣言传播和真实信息传播的时间间隔对两类信息扩散的影响。

部分研究考虑了时间因素，如Cheng等^[8]考虑了控制策略对谣言的影响，提出了谣言传播规模最小的最优控制问题，比较了时间延迟、最优控制和媒体网络对谣言传播的影响。Zan等^[9]发现新谣言存在明确的最佳传播时间，并通过仿真结果得出了双重谣言传播模式。Amirhosein等^[10]首先假设随着时间的推移谣言逐渐失去影响力，仿真验证了Twitter上谣言扩散的真实数据。Qian等^[11]采用独立扩散者的概念来研究用户获得谣言的途径，结果发现在无标度网络中，当中心节点成为传播者时，更容易广泛地传播谣言。Qiu^[12]考虑了外部的权威因素和用户遗忘、以及用户行为受时间影响等因素，针对SIR模型来研究这些因素对谣言传播的影响。王家坤等^[13]考虑到谣言的时效性和用户追随性等特征，研究了一种基于线性阈值的谣言离散传播模型。

一部分研究从节点或用户角度来进行，例如，张金鑫等^[14]考虑了网络中多个传播谣言的节点因素，Hu等^[15]根据态度将谣言传播者分成3类，结果发现，不同态度对谣言传播具有不同的影响，但对谣言态度犹豫不决的人会对谣言传播有积极的影响。Indu等^[16]提出了一种算法来识别谣言传播过程中起主要作用的节点。Tian等^[17]提出了一种新的谣言传播模型ILRD，该模型假定一个未知者在和传谣者以及辟谣者联系后，对谣言的态度有3种可能性。Yang等^[18]考虑了不同用户在谣言传播中的作用，提出了一种新的描述谣言传播过程的模型。Adil等^[19]考虑人的因素如个人立场、社会影响、行为等，提出了HISB模型和一种活动策略，结果发现无论是在单个网络中还是在多个网络中，都能有效地减少谣言的影响。Bodaghi等^[20]根据推特上的谣言来研究谣言传播过程中的用户特征和基本模式，发现大多数用户只参与一次谣言传播，且谣言传播与反谣言传播的间隔时间较大程度地影响谣言扩散。Mojgan等^[21]提出了一个谣言控制模型，研究认为向自己信任的朋友询问可以避免谣言的传播，实验结果表明该机制在某些情况下可以更好地控制谣言传播。

除此之外，Virginia等^[22]在DK模型中引入了以一定速率发生的否认因素来研究谣言传播，通过数值分析研究各类节点的变化规律。Zhao等^[23]在SIR模型基础上引入了传播力参数来描述谣言传播过程中的不确定性。Xia等^[24]考虑谣言内容的吸引力和模糊性以及遗忘因素，提出了一种新的谣言扩散模型，结果表明降低谣言内容的模糊度可以有效降低谣言的影响范围。Zhang等^[25]考虑了群体结构的影响来研究谣言传播，结论表明社区群体规模越大，谣言扩散速度也越大。Jia等^[26]提出了一个具有潜伏期的社交网络谣言扩散模型，对谣言的传播路径、重新分享谣言的节点以及对谣言传播起关键作用的节点进行研究，并利用微分方程的方法证明了模型的准确性。Huo等^[27]考虑到媒体报道对谣言传播的影响，提出了一个新的非线性谣言数学模型。

对上述已有研究成果进行分析发现，尚未有学者结合真实信息发布的滞后性来研究真实信息和虚假信息的竞争扩散问题。虚假信息的扩散對企业的发展和人们的日常生活会产生不利影响，相关部门针对虚假信息在网络中的扩散，有必要发布真实的信息进行反驳澄清，从而抑制虚假信息进一步扩散。现实中存在这种现象，即虚假信息扩散一段时间后，真实信息才开始在网络中扩散。例如，新冠病毒疫情刚开始传播时，“双黄连可以预防新冠病毒”的虚假信息被许多网民相信并传播，随后相关部门和人员发布了真实信息进行纠正。在一段时间内，真实信息和一些负面的谣言、诈骗等虚假信息呈现一种共同竞争扩散的现象。

本文在考虑实际现象和以往研究的基础上，提出一种真实信息与虚假信息竞争扩散的模型，分析真实信息的扩散时间滞后于虚假信息时，哪些因素对两类信息的扩散比例有明显的影响。该模型有两点不同之处：1）虚假信息在网络中传播一段时间后，加入一类传播真实信息的节点，该节点会影响传播虚假信息的节点，两种信息在社会网络中竞争扩散。2）不同于一些研究只设立一类免疫节点，本文对相信虚假信息的节点和相信真实信息的节点进行区分，因此，虚假信息扩散所导致的最终影响范围可以更加具体。

1 信息扩散规则及模型

初始状态下，网络中只有一个节点S_F扩散虚假信息F，其余的为不知道任何一种信息的未知信息节点I。

考虑到虚假信息的扩散一般要早于真实信息，在一段时间内，网络中仅虚假信息F扩散，模型如图1所示。假定虚假信息扩散一段时间后，真实信息才开始扩散，网络中有一个节点S_T扩散正面信息T来反驳虚假信息F，二者在社会网络中共存一段时间，可构建一个竞争扩散模型，如图2所示。因此，两种信息扩散后，网络中节点可能会具有5种状态，分别是未知信息节点I、扩散虚假信息的节点S_F、扩散真实信息的节点S_T、相信信息F的节点B_F和相信信息T的节点B_T，B_T或B_F都分别不会扩散信息T或F。

具体的信息扩散规则为：1）图1中，随机选择的扩散节点S_F扩散信息F后，它的未知信息的邻居节点I以q_F的概率成为S_F，或者以p_F的概率成为B_F。节点S_F扩散信息F后，以β_F的概率成为B_F。2）在虚假信息扩散一段时间后，网络中加入一个随机选择的扩散节点S_T扩散真实信息T，来对虚假信息进行反驳以减少社会影响，它的未知信息的邻居节点I以q_T的概率成为S_T，或者以p_T的概率成为B_T。同时，虚假信息F也继续扩散，扩散节点S_F扩散信息F后，它的未知信息的邻居节点I以q_F的概率成为S_F，或者以p_F的概率成为B_F。3）扩散节点S_T也有可能接收到S_F扩散的虚假信息F，但扩散节点S_T扩散的是真实信息T，其不会成为扩散节点S_F。节点S_T扩散信息T后，以β_T的概率成为B_T。4）扩散节点S_F有可能接收到S_T扩散的真实信息T，并认识到之前信息内容的错误，因此扩散节点S_F以α的概率成为扩散节点S_T或者以θ的概率成为节点B_T。节点S_F扩散信息F后，以β_F的概率成为B_F。5）节点B_F有可能还会接收到扩散节点S_T所发送的真实信息，因此以概率γ成为节点B_T；节点B_T有可能还会接收到扩散节点S_F所发送的信息F，但它不会相信信息F的内容，因此不会成为节点B_F。6）信息扩散后，网络中增加了两类节点，分别是知道且相信真实信息T的节点B_T和知道且相信虚假信息F的节点B_F，B_T或B_F都分别不会再去扩散信息T或F。

模型微分方程为

其中，k为网络的平均度，τ为真实信息延迟扩散的时间。基本再生数为再生矩阵的谱半径FV^-1，且当ρ（FV^-1）<1时，无信息平衡点局部渐进稳定。结合方程组（1）可知（1，0，0，0，0）是该系统的无信息扩散平衡点，在该平衡点处求解矩阵F和V。

2 实验仿真及分析

本文利用Matlab R2014a在小世界网络上进行仿真实验，初始条件下，网络节点数N=4 000，平均度为8，重连概率为0.5，q_T=0.4，p_T=0.4，β_T=0.5，q_F=0.2，p_F=0.4，β_F=0.5，α=0.5，θ=0.4，γ=0.6。假设真实信息要比虚假信息延迟t个时间单位（t分别取1、5和15）才开始扩散，信息扩散过程持续30个时间单位，在相同参数下，实验重复1 000次并取均值。

2.1 基本再生数检验

首先验证模型的基本再生数。令β_T=β_F=0.8，考虑两种场景，一是令q_F=0.05，将q_T值从0.01增大到0.25，根据上文，当q_T=0.1时，基本再生数为1；二是令q_T=0.05，将q_F值从0.01增大到0.25，当q_F=0.1时，基本再生数为1。网络中两类信息扩散比例达到稳态时，其扩散比例之和如图3所示。可見，比例之和在q_T≤0.1或q_F≤0.1时近似为0，大于0.1时则显著增加，可证明计算的基本再生数正确。

2.2 真实信息的不同起始扩散时间对信息扩散范围的影响

设真实信息T分别延迟1、5和15个时间单位开始扩散，从图4可知，真实信息扩散的时间越早，其扩散范围越大，虚假信息扩散的范围越小。还可以看出，真实信息扩散的范围是否大于虚假信息与真实信息的起始扩散时间有关：t=1时，真实信息扩散范围基本上一直大于虚假信息；t=5时，真实信息扩散范围在扩散时间持续到11时才大于虚假信息；t=15时，真实信息扩散范围基本上和虚假信息一致。因此，对于舆情管控部门，尽早发布真实准确的信息有助于减少虚假信息的扩散范围。

2.3 q_T和q_F对信息扩散范围的影响

图5a中真实信息延迟5个时间单位开始扩散。当q_T=0.6时，可见q_F的增加对真实信息扩散的比例有一定的抑制，且与虚假信息扩散比例的变化趋势相反。当q_F=0.4时，随着q_T逐渐增加，相比较于前述q_T不变时q_F逐渐增加，真实信息扩散比例较小幅度地逐渐增加，虚假信息扩散比例减少不明显。因此可以表明，q_F的变化对两类信息扩散范围的影响要超过q_T的变化对两类信息扩散范围的影响。

图5b中真实信息延迟1个时间单位开始扩散，图5a中，真实信息延迟5个时间单位时，只有改变q_F才会对真实信息的扩散范围产生显著影响，而改变q_T几乎不影响虚假信息的扩散范围。与图5a不同的是，在图5b中，当q_T和q_F这二者增加时，分别会明显减少另外一种信息的扩散比例。这不同于在正面信息延迟扩散且延迟时间较久时，应采取措施来降低未知节点成为扩散虚假信息节点的可能性；而当正面信息延迟时间较短时，采取措施来降低未知节点成为扩散虚假信息节点的可能性或者增加未知节点成为扩散真实信息节点的可能性，均有较明显的效果。

2.4 β_T和β_F对两类信息扩散比例的影响

如图6所示，真实信息延迟1个或5个时间单位时，增加β_T值，真实信息的扩散比例均明显增加，相比而言，虚假信息扩散比例的变化范围较小。改变β_F值时，真实信息扩散比例的变化较小，且变化幅度要小于虚假信息扩散比例的变化幅度。

2.5 p_T和p_F对两类信息扩散比例的影响

在图7中，真实信息较早扩散，改变p_T对其扩散比例有一定的影响，而改变p_F对虚假信息的扩散比例影响有限。真实信息初始扩散时间在延迟5个时间单位时，其扩散比例随p_T的增加而增加，虚假信息扩散比例变化幅度则较小。将p_F值逐渐增大，两图中均出现了真实信息扩散比例先减少后增加的现象。总体而言，改变p_T和p_F的值对网络中两类信息扩散比例的影响有限。

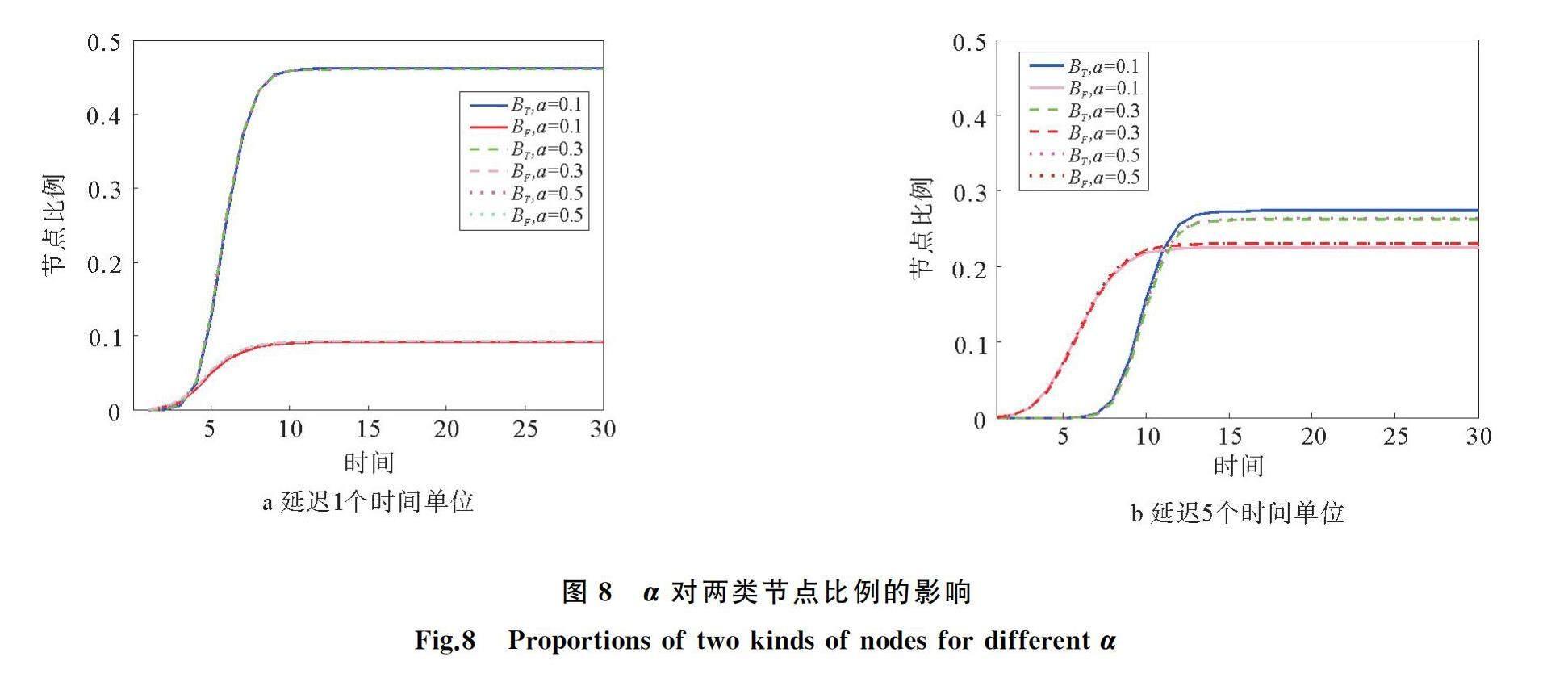
2.6 α对信息扩散范围的影响

增加扩散虚假信息的节点成为扩散真实信息节点的概率，理论上使扩散真实信息的节点增加，从而增加真实信息的扩散范围。但从图8来看，改变α对两类信息的最终扩散范围几乎没有任何影响，这可能是由于扩散节点在网络中的占比很低。因此，采取措施使传播虚假信息的节点转而去传播真实信息的效果不够明显。

2.7 初始的S_T数量对信息扩散范围的影响

从图9a中可知，真实信息初始扩散时间滞后5个时间单位，即使逐渐增加初始扩散真实信息的节点数量，对两类信息最终扩散范围的影响仍十分有限。但在图9b中，真实信息初始扩散时间延后了1个时间单位，改变初始节点数量，对最终扩散范围有较明显的影响。因此，对管控虚假信息扩散范围而言，需要在早期增加初始传播真实信息的节点数量。随着时间延长，即使增加传播真实信息节点数量，减少虚假信息扩散范围和扩大真实信息扩散范围的效果也会变差。

2.8 网络平均度和规模对信息扩散范围的影响

在图10中，真实信息的初始扩散时间延迟1个时间单位，在不改变网络规模的情况下，增加网络平均度，可以发现真实信息与虚假信息的扩散比例均明显增加，这是由于度的增加会使两类信息的扩散节点将信息扩散给更多未知信息节点。而增加网络规模但不改变平均度时，真实信息的扩散比例增加较小，相反，虚假信息的扩散比例则减少，比例变化也很小。

当真实信息的初始扩散时间延迟5个时间单位，仅增加网络平均度时，真实信息的扩散比例明显减少，而虚假信息的扩散比例则明显增加。但仅改变网络规模时，两类信息的扩散比例没有明显变化。这是因为真实信息还未扩散时，虚假信息就因为网络平均度的增加，得到了更大范围的扩散，使得虚假信息扩散节点的数量增加较多，如在第5个时间单位时，虚假信息节点的比例增加较多，从而抑制了真实信息的扩散。

2.9 真实信息初始扩散节点的度值对信息扩散范围的影响

图11中，在初始参数下，选择网络中度最大的节点作为扩散真实信息的节点，对比图4可知，延迟5个时间单位时，真实信息的扩散比例增加幅度明显，虚假信息的扩散比例减少但幅度相对要小。同样，在延迟15个时间单位时，真实信息的扩散比例同样也增加，且超过了虚假信息的扩散比例，虚假信息扩散比例变化不明显。管理者选择度最大的节点扩散真实信息，有利于获得舆论优势，同时减少虚假信息的扩散范围，但随着时间推迟，真实信息在网络中所占的比例优势逐渐变小，虚假信息所占的比例逐渐变大。因此即使选择度更大的节点来扩散真实信息，也应尽早进行。

3 结论

本文考虑了社会网络中先有虚假信息扩散而后才有相关真实信息扩散的实际现象，构建了一个真实信息扩散时滞的两类信息竞争扩散模型。模型考虑了扩散虚假信息的节点受到影响并相信真实信息，从而转变成为扩散真实信息的节点，研究发现该因素的影响十分有限。考虑到相关部门要扩大真实信息的扩散范围并抑制虚假信息的扩散范围，仿真结果显示，应尽可能较早地在网络中扩散真实信息，增加初始扩散时真实信息节点的数量或选择度较大的节点来扩散真实信息，采取措施降低未知节点成为扩散虚假信息节点的可能性或增加未知节点成为扩散真实信息节点的可能性。但如果虚假信息在网络中扩散了较长时间后才开始扩散真实信息，可选择的方式比较有限，即降低未知节点成为扩散虚假信息节点的可能性，且效果不够显著。

本文的研究设定在同一个社会网络中，实际上真实信息和虚假信息可能在多个社会网络中不同的时间点开始扩散，在多层社会网络中考虑真实信息扩散的时滞因素来研究真实信息和虚假信息的竞争扩散是我们下一步的研究目标。

参考文献：

[1]ZHU L H， YANG F， GUAN G，  et al. Modeling the dynamics of rumor diffusion over complex networks[J]. Information Sciences， 2020， 562（1）： 240-258.

[2]朱霖河， 李玲. 基于辟谣机制的时滞谣言传播模型的动力学分析[J]. 物理学报， 2020， 69（2）： 020501.

ZHU L H， LI L. Dynamic analysis of rumor-spread-delaying model based on rumor refuting mechanism[J]. Acta Physica Sinica， 2020， 69（2）： 020501.

[3]HUANG H， CHEN Y H， MA Y F. Modeling the competitive diffusions of rumor and knowledge and the impacts on epidemic spreading[J]. Applied Mathematics and Computation， 2021， 388： 125536.

[4]JIANG M L， GAO Q W， ZHUANG J. Reciprocal spreading and debunking processes of online misinformation： a new rumor spreading-debunking model with a case study[J]. Physica A， 2021， 565（1）： 125572.

[5]MA J， LI D D， TIAN Z H. Rumor spreading in online social networks by considering the bipolar social reinforcement[J]. Physica A， 2016， 447： 108-115.

[6]HUO L A， SONG N X. Dynamical interplay between the dissemination of scientific knowledge and rumor spreading in emergency[J]. Physica A， 2016， 461： 73-84.

[7]張菊平， 郭昊明， 荆文君，等. 基于真实信息传播者的谣言传播模型的动力学分析[J].物理学报， 2019， 68（15）： 150501.

ZHANG J P， GUO H M， JING W J， et al. Dynamic analysis of rumor propagation model based on true information spreader[J]. Acta Physica Sinica， 2019， 68（15）： 150501.

[8]CHENG Y Y， HUO L A， ZHAO L J. Dynamical behaviors and control measures of rumor-spreading model in consideration of the infected media and time delay[J]. Information Sciences， 2021， 564（1）： 237-253.

[9]ZAN Y L. DSIR double-rumors spreading model in complex networks[J]. Chaos， Solitons & Fractals， 2018， 110： 191-202.

[10] AMIRHOSEIN B， SAMA G， MOSTAFA S. The number of followings as an influential factor in rumor spreading[J]. Applied Mathematics and Computation， 2019， 357： 167-184.

[11] TANG S T， QIAN Z， ZHANG X， et al. The independent spreaders involved SIR rumor model in complex networks[J]. Physica A， 2015， 429： 95-102.

[12] QIU X Y， ZHAO L J， WANG J J， et al. Effects of time-dependent diffusion behaviors on the rumor spreading in social networks[J]. Physics Letters A， 2016， 380 （24）： 2054-2063.

[13] 王家坤， 王新华. 一种基于线性阈值的网络谣言离散传播模型[J]. 情报科学， 2019， 37（6）：163-169.

WANG J K， WANG X H. A discrete propagation model of internet rumor based on linear threshold[J]. Information Science， 2019， 37（6）： 163-169.

[14] 张金鑫， 王丽婷， 张金华. 具有多个传播源的网络谣言传播与导控模型研究[J]. 情报科学， 2020， 38（11）： 115-120.

ZHANG J X， WANG L T， ZHANG J H. Internet rumors spreading and control model with multiple propagation sources[J]. Information Science， 2020， 38（11）： 115-120.

[15] HU Y H， PAN Q H， HOU W B， et al. Rumor spreading model with the different attitudes towards rumors[J]. Physica A， 2018， 502： 331-344.

[16] INDU V， THAMPI S M. A nature-inspired approach based on Forest Fire model for modeling rumor propagation in social networks[J]. Journal of Network and Computer Applications， 2019， 125： 28-41.

[17] TIAN Y， DING X J. Rumor spreading model with considering debunking behavior in emergencies [J]. Applied Mathematics and Computation， 2019， 363： 124599.

[18] YANG A Z， HUANG X Y， CAI X M， et al. ILSR rumor spreading model with degree in complex network[J]. Physica A， 2019， 531： 121807.

[19] AIEHA B， KAN L A， SAA C. Minimizing rumor influence in multiplex online social networks based on human individual and social behaviors[J]. Information Sciences， 2020， 512： 1458-1480.

[20] BODAGHI A， OLIVEIRA J. The characteristics of rumor spreaders on twitter： a quantitative analysis on real data[J]. Computer Communications， 2020， 160： 674-687.

[21] ASKARIZADEH M， LADANI B T. Soft rumor control in social networks： modeling and analysis[J]. Engineering Applications of Artificial Intelligence， 2021， 100（10）： 104198.

[22] VIRGINIA G， SERENA S. Rumor spreading models with random denials[J]. Physica A， 2016， 461： 569-576.

[23] ZHAO Z J， LIU Y M，WANG K X. An analysis of rumor propagation based on propagation force[J]. Physica A， 2016， 443： 263-271.

[24] XIA L L， JIANG G P， SONG B， et al. Rumor spreading model considering hesitating mechanism in complex social networks[J]. Physica A， 2015， 437： 295-303.

[25] ZHANG R X， LI D Y. Rumor propagation on networks with community structure[J]. Physica A， 2017， 483： 375-385.

[26] JIA J W， WU W J. A rumor transmission model with incubation in social networks[J]. Physica A， 2018， 491： 453-462.

[27] HUO L A， WANG L， ZHAO X M. Stability analysis and optimal control of a rumor spreading model with media report[J]. Physica A， 2019， 517： 551-562.

（責任编辑 耿金花）