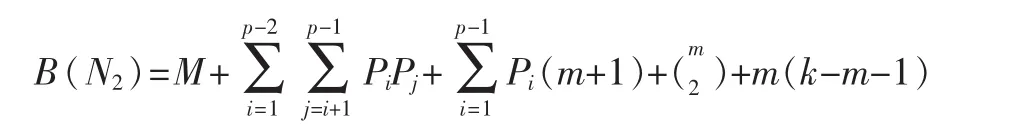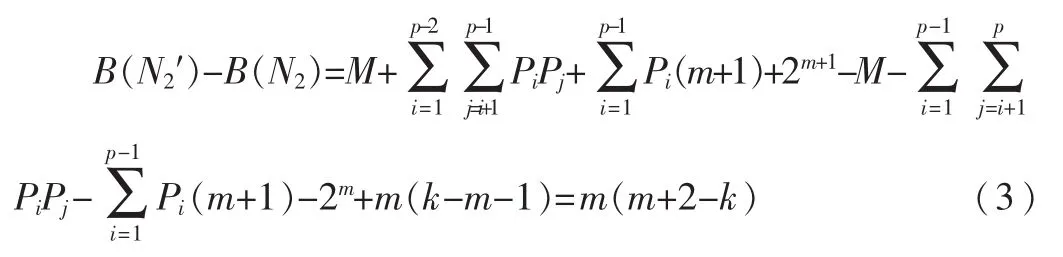树形网络的平均介数*
霍慧鸣,赵海兴
(青海师范大学 计算机学院,青海 西宁 810008)
自从20世纪30年代Radcliffe Brown提出社会网络分析概念以来,社会网络分析已经逐步成为一种重要的社会定量研究方法[1]。近年来,随着计算机技术和互联网的飞速发展,如何利用文本挖掘、机器学习等技术面向互联网进行社会网络挖掘和分析成为了一个新的研究课题。随着数据挖掘技术的进步以及计算机处理能力的提高,研究者们分析的社会网络的规模也急剧增大。这些分析和其他现实网络分析一样,面临网络节点规模巨大的挑战。
现实生活中存在的大量复杂系统都可以通过不同的网络加以描述,网络科学已成为众多学科汇聚的交叉点。复杂网络是近几年科学研究发现的一种介于规则网络和随机网络之间的一种更接近于真实网络的网络模型,钱学森给出了复杂网络的一个较严格的定义:具有自组织、自相似、吸引子、小世界、无标度(无尺度)中部分或全部性质的网络称为复杂网络[2]。随着复杂网络规模的不断扩大,对于各个节点在整个图中所起作用的研究变得迫切,各个节点的作用可以用介数来表示。介数既能刻画图中节点和边的重要性,揭示网络层次结构,又能用来构建基于点介数或边介数的聚类算法,发现图中特殊群体,因此,它一直是研究网络结构性质的一个重要量化手段。首先对于介数的概念要有一定的了解。在复杂网络研究中,研究者不仅要非常客观地关注系统内个体之间的相互作用,而且还要注视系统的整体相互作用,表达这种整体相互作用的概念是介数。介数是一个全局的变量,反映节点或边的作用和影响力,可分为节点介数(Vertex Betweenness)和边介数(Edge Betweenness)两种。节点介数定义为在网络的所有最短路径中,通过节点的最短路径条数称之为节点i的介数[3];边的介数定义为在网络的所有最短径经过边的介数;网络平均节点介数定义为网络中所有节点介数的平均值;网络平均边介数指网络中所有边介数的平均值。节点的介数在一定程度反映的是节点在网络中的核心作用,节点的介数越大,表明节点的核心作用越强,删除这样的节点会使大量节点对之间的最短路径变长,边的介数也有同样的性质。
本文主要讨论树形网络的平均节点介数,其中节点介数是经过该节点的所有路径,网络平均节点介数是指所有节点介数的平均值。下面举一个具体的例子来分析节点介数和边介数。图1所示中各节点与边的介数可以分别表示如下。

图1 节点介数与边介数关系图
表1中的平均节点介数为4.375,平均边介数为7.25,依据Newman[4]提出的介数新的计算机方法和Brandes算法可以更快地计算出介数。更多的介绍见参考文献[5-7]。
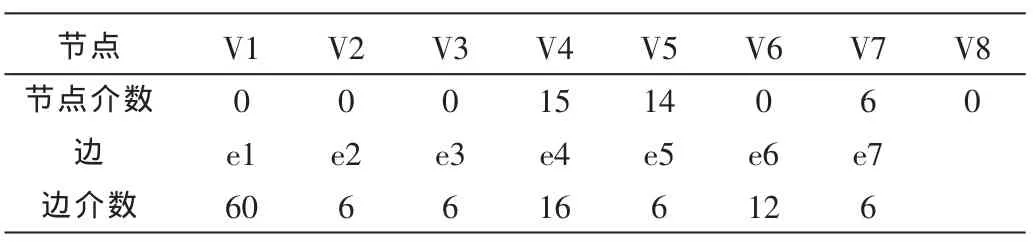
表1 各节点介数与边介数的关系
本文研究了树形网络中平均节点介数最大的图和最小的图,所有树的平均节点介数小于路的平均节点介数和其大于星形图的节点平均介数。
复杂网络树形图中的介数源于网络中对个体重要性的评估,一个节点介数表示所有节点对之间通过该节点的最短路径条数,因此它能够刻画节点在网络中的重要程度,任意节点v的介数值定义为[8]:
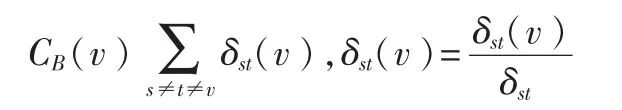
其中,δst为节点 s 到 t的最短路径数目,δst(v)为节点 s 到t的最短路径中经过节点v的最短路径数目。
树形网络中节点介数就是通过该节点的路径数目。如有一个n个节点的树形网络 N,节点用v表示,平均节点介数可表示为:
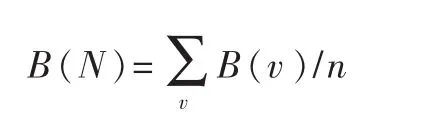
1 树形网络中最大平均节点介数图
随着复杂网络规模的不断增加,节点数目也在不断地增加,对于一些冗余的节点删除变得更加必要,这就需要对于节点的作用给出一个正确的评估,需要了解哪些图形具有最大的平均节点介数,网络结构可以尽可能地向这样的结构变化。本节主要介绍具有最大平均节点介数的网络。
引理 1 如图 2所示,N1是一棵树,N1′是经过图 2的变换得到的,则等号成立当且仅当N1是一条路。
证明 有k个节点的图,如图2所示,图N1中节点A上有p个分支,有n个节点的为分支P1,有m个节点的为分支P2。图N1把分支P1添加到分支P2之后得到图的N1′分支P1+P2。则节点A上变成了P-1个分支。因为分支节点介数与分支结构和总节点个数有关,现在树形图 N1和 N1′的平均节点介数 B(N1)和 B(N1′)中,图 N1和 N1′中除了节点 A, 分支 P1、P2及分支 P1+P2的节点介数有变化,其他分支对应节点介数都没有改变。把其他分支节点的介数之和用M表示。

图2 N1 与 N1′的关系图
图N1上节点介数分别表示如下:

表2 分支P1各节点介数

表3 分支P2各节点介数
平均节点介数为:

图N1′中节点介数分别表示如下:

表4 分支P1+P2的介数
平均节点介数可以表示为:

将变化前后的两个图的平均介数进行比较,比较结果为:
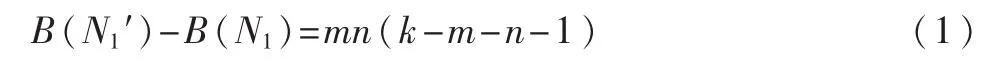
由式(1)知,k≥m+n+1,B(N1)≤B(N1′),等号成立当且仅当 N1是一条路时,故可得 B(N1)≤B(N1′),证毕。
路是各个节点的度不大于2的连通的无圈图,两端的两个点的度为1,中间的各个节点的度均为2。n个节点的路中两端的两个节点为1度的叶子节点,其介数为0。假如第 i个节点的介数,i的取值范围是1~n,各个节点的介数可以表示为(n-i)(i-1),其平均介数为:
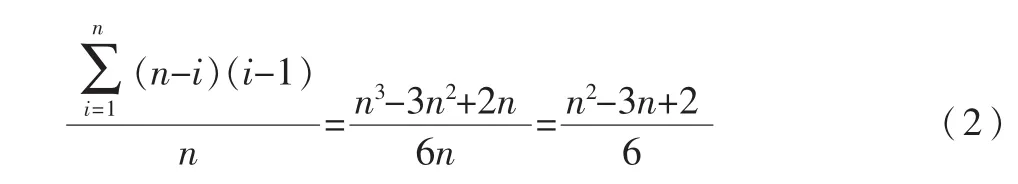
定理1 路是具有最大平均节点介数的树形图,n个节点的平均介数为:。
证明 用归纳法证明如下。
(1)当n=4时,有4个节点的图只有两种形式,即路和星形图,路的平均节点介数为1,星形图的平均节点介数为0.75,路具有较大的平均节点介数,成立。
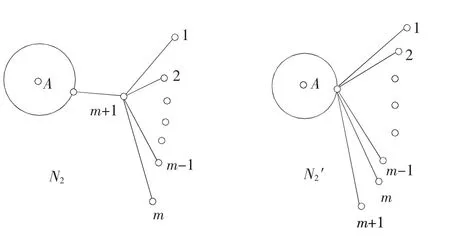
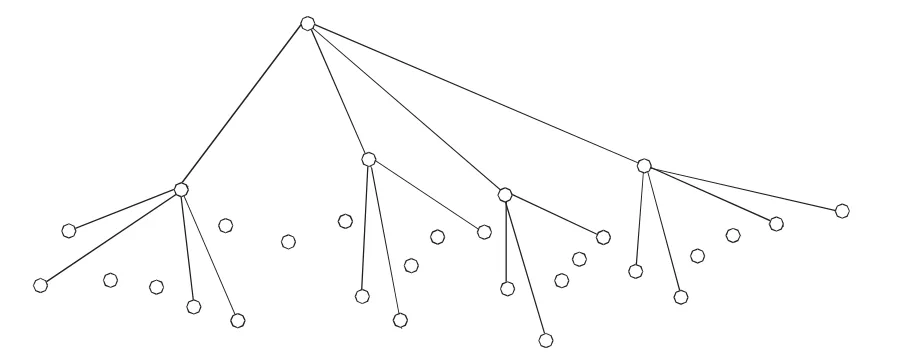
(2)假如对于n 图3 n 综上所述,在树形图中,路具有最大的平均节点介数,证毕。 本节主要研究树形网络的结构中具有最小的平均节点介数。对此可以知道哪些结构的网络中节点的相对作用较小,删除这样的节点的分支,对于整个的网络影响相对不大。 引理 2 如图 4所示,N2所示是一棵树,N2′是由 N2把图4所示的1度点分支添加到节点A得来的,则B(N2)≥B(N2′),等式成立当且仅当 N2是一个星形图。 图4 树形网络中节点分析图 证明 假如对于图4所示的N2中节点A有p个分支,k个节点的图,图中有一个m个1度点的分支。图N2′把图N2中m个1度的点添加到节点 A上,分支变成了1度点。节点A的分支个数变成了p+m个。图N2和N2′中的平均节点介数用 B(N2)和 B(N2′)表示。 N2和 N2′中m个1度点的介数仍然为零,没有改变。其中,除了节点A、节点m+1有变化,其他p-1个分支对应节点介数都没有改变。未改变的分支节点介数和用M表示。 图N2改变的节点介数和为: 图 N2′的节点介数和为: 用 B(N2)减去 B(N2′)等式可得: 由式(3)可知,k≥m+2 时,有 B(N2)≥B(N2′)成立,等号成立当且仅当是一个星形图时。其他情况都是k>m+2,故引理可证,证毕。 星形图是只有一个节点的度不为1,其他节点的度都为1的图。星形图中,度为1的节点的介数都是0,在星形图中,称这个有最大度的节点为Hub节点,也只有这么一个节点的介数不是0。假如有n个节点的星形图,其中有n-1个节点的介数为0,Hub节点的介数为:。故有n个节点的星形图的平均节点介数为:/n=。 定理2 星形图具有最小的节点平均节点介数,n个节点的星形图的平均节点介数为:。 证明 用归纳法证明如下。 (1)当n=4时,有4个节点的图只有两种形式,即路和星形图,路的节点平均介数为1,星形图的节点平均介数为0.75,星形图有最小平均节点介数,成立。 (2)假设当n 图5 树形网络具有最小平均节点介数的图 综上所述,星形图具有最小的平均节点介数,证毕。 本文主要讨论了在复杂网络中树形网络的平均节点介数最大和最小的网络,对于与之相关节点介数增加和减少给出了两个引理,节点介数是通过该节点的路径数。更多的介数应用和算法分析可以参考文献[9]~[11]。 [1]SCOT J.Social network analysis: a handbook (2nded)[M].Sage Publications,1991. [2]张嗣瀛.复杂系统与复杂性科学[EB/OL].http://news.qdu.edu.cn/newx? newsid=1514,2006-05-05. [3]张晓林,袁莉,杨峰,等.基于 Web的个性化信息服务机制[J].现代图书情报技术,2001(1):25-29. [4]NEWMAN M E J.Scientific collaboration networks.II.shortest paths, weighted networks, and centrality[J].Phys.Rev.E, 2001, 64(1). [5]LEWIS T G.网络科学原理与应用[M].陈向阳,巨修红练,译.北京:机械工业出版社,2011. [6]马杰良,邢雪,安莉莉.基于科研合作网络的节点枢纽特性研究[J].东北电力大学学报,2008,28(2):72-76. [7]Zhang Z Z, Zhou S G, Y Qi, et al.Topologies and laplacian spectra of a deterministic uniform recursive tree[J].Eur, Phys, J.B, 2008(63):507-513. [8]唐晋韬,王挺.复杂社会网络的介数性质近似计算方法研究[J].计算机工程与科学,2008,30(12):9-14. [9]王小光,王锋,李森.基于介数影响矩阵的通信网络节点重要度评价方法[J].空军工程大学学报,2012,13(5):80-84. [10]何宇,赵洪利,姚曜,等.介数中心性和平均最短路径长度整合近似算法[J].复杂系统与复杂性科学,2011,8(3):44-53. [11]贾炜,冯登国,连一峰.基于网络中心性的计算机网络脆弱性评估方法[J].中国科学院研究生学报,2012,29(4):529-535.
2 树形网络中具有最小平均节点介数的图