基于深度学习的探究课实践
张山峰


摘 要:本文借助《二次函数与一元二次方程、不等式》这一高中数学探究课的教学实践与应用,结合深度学习的基本效益、课堂实践以及教学启示等方面,合理展开,阐述深度学习下探究课的基本教学实践与尝试,合理创新与应用于教学实践.
关键词:深度学习;函数;方程;不等式
深度学习,是一个源于人工神经网络研究的概念,也是实现人工智能的必经路径,对于学生的实际学习也有很大的借鉴与帮助作用.在课堂教学与学习实践中,合理与适度的深度学习,对知识的联系与拓展,深入与应用等方面都有着非常大的帮助,特别对一些涉及数学探究课的教学有时更能展示其重要作用.
1 深度学习的基本效益
1.1 增强概念的深层理解
在数学概念教学与学习过程中,借助深度学习,可以深入挖掘概念的内涵与实质以及实现概念的外延与应用.同时,比较相关概念、相似概念以及不同概念之间的联系,对于概念的深层理解有很大的效益.
1.2 探究问题的来龙去脉
在数学探究教学与学习过程中,借助深度学习,可以更好地挖掘、探究问题的本质、从问题的横向、纵向等方面展开,深入学习与之相关的数学基础知识,也为问题的进一步拓展与应用提供条件.
1.3 形成知识的交汇融合
在数学知识的构建与形成过程中,借助深度学习,可以合理构建更加系统与全面的数学知识网络体系,形成各个数学知识点之间的联系与转化,以及不同知识点之间的交汇与融合,更加有效地提升学生的数学能力.
2 深度学习的课堂实践
2.1 导学聚焦
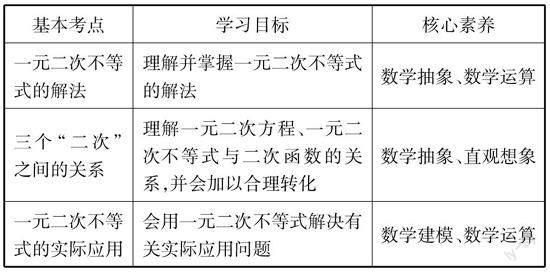
在实际高中数学课堂教学与学习时,厘清本节课的学习目标对应的基本考点以及相应的数学核心素养等,可以非常有效地为数学课堂的探究教学确定明确的教学与学习目标,构建对应的数学理念,紧紧围绕相应的教学与学习目标来达到目的.
2.2 问题导学
预习教材必修第一册(人民教育出版社2019年版)第二章《一元二次函数、方程和不等式》中的第三小节:《2.3 二次函数与一元二次方程、不等式》并思考下列相关问题:
(1) 一元二次不等式的概念是什么?
(2) 二次函数与一元二次方程、一元二次不等式的解有什么对应关系?
(3) 求解一元二次不等式ax2+bx+c>0(a>0)的過程是什么?
学生带着问题去自主学习与自主探究,这其实是课堂教学中比较常见的基本方式,但这也为开拓学生的数学思维与提升学生的数学能力等提供条件,为进一步的深度学习起到自然过渡与引导的作用.借助学生的自主学习与自主探究,通过课堂教学的探究课教学的深入与应用,可以更加有效地提升深度学习的效果.
2.3 新知探究
2.3.1 一元二次不等式
(1) 一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
借助一元二次不等式的解法及其应用,从涉及一元二次不等式问题的多个视角与多个层面展开,通过以上四个方面加以实例剖析,为具体问题的一元二次不等式的解法及其应用提供条件,实现深度学习的根本目的.
3 深度学习的教学启示
3.1 立足探究,深度融合
基于数学探究课教学中的深度学习,结合数学基础知识与基本概念的探究与学习,可以采用多层面的视角,结合相应的教材内容与课堂实践,从横向或纵向等方面加以联系与教学推进,培育学生的综合能力和创新意识.基于此,通过深度学习,强化、巩固数学基础,进而进行合理的变式与探究以及拓展应用,从不同维度探究求解策略,提炼解题方法,真正有效地加以深度融合,形成一个更加完善的知识体系.
3.2 把握实质,提升能力
基于数学探究课教学中的深度学习,往往更加注重数学基础知识的内核与精髓.通过深度学习,经常可以将孤立、碎片化的知识串点成线、织网铺面,在此过程中建构创新,培养学生的创新意识与创新能力,同时夯实学生的“四基”,培养学生的“四能”,培育理性思维,促进学生高阶思维、核心素养的发展.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018.

