圆锥曲线综合测试卷（A 卷）答案与提示

一、选择题

1.C2.D3.A4.D5.B

7.B 提示:设椭圆的左焦点为E,连接AE,BE。因为AF⊥BF,所以四边形AEBF为矩形,∠EAF=90°,∠ABF=∠AEF,|AF|=2csinα,|AE|=2ccosα。

8.D 提示:假设A在第一象限,如图1。

图1

过A,B分别向抛物线的准线作垂线,垂足分别为D,E。

过A作EB的垂线,垂足为C,则四边形ADEC为矩形。

由抛物线定义可知|AD|=|AF|,|BE|=|BF|。

又因为|FA|=3|FB|,所以|AD|=|CE|=3|BE|,即B为CE的三等分点。

设|BF|=m,则|BC|=2m,|AF|=3m,|AB|=4m。

10.D 提示:如图2 所示,分别过点A,B作准线的垂线,垂足分别为E,M,连接EF。抛物线C的准线交x轴于点P,则|PF|=p。由于直线l的斜率为,故其倾斜角为60°。又AE∥x轴,故∠EAF=60°。由抛物线的定义可知,|AE|=|AF|,则△AEF为等边三角形,∠EFP=∠AEF=60°,∠PEF=30°。所以|AF|=|EF|=2|PF|=2p=8,解得p=4,故A正确。

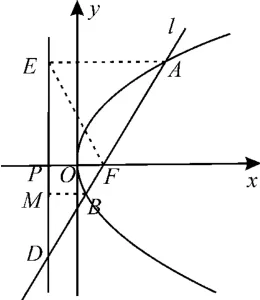
图2

因为|AE|=|EF|=2|PF|,PF∥AE,所以F为线段AD的中点,则故B正确。

因∠DAE=60°,故∠ADE=30°,|BD|=2|BM|=2|BF|(抛物线定义),故C正确。

因为|BD|=2|BF|,所以|BF|=,D 错误。

11.B 提示:由题意可知,直线l的方程

二、填空题

16.④

提示:设P(x0,y0),过点P与AB平行的直线为l。

要使△ABP的面积最大,只需点P到AB的距离最大。

而P点是抛物线的弧AOB上的一点,故点P是抛物线上平行于直线AB的切线的切点。

三、解答题