灵动思维 创新突破

黄红

【摘要】初中数学课程以创新、灵活为突出特征，要求教师打破教学惯性思维，开拓创新空间，培养学生的综合能力.与之相对应的，逆向思维在理论与实践中的灵活运用便更具重要意义.文章聚焦初中数学教学中的逆向思维核心问题，从概念解析入手，分析培养学生逆向思维能力的可行性与必行性，进而就教学实例多维度探讨其具体培养策略，层层深入，以期为广大教学工作者提供经验借鉴.

【关键词】逆向思维；初中数学；创新思维；策略分析

【基金项目】本文系2020年度广东省教育研究院教育教研课题《通过专业阅读提升初中数学教师专业素养的实践研究》（课题批准号：GDJY-2020-A-s079）的阶段性研究成果.

随着新课改的不断深入以及“双减”政策的持续贯彻落实，初中数学教学面貌已焕然一新.作为一项创新性教学策略，“逆向思维”的引入与实施是落实新教育观念与教学方法的重要途径.因此，数学教师应明确逆向思维的重要性，并将其融入具体的题目分析之中，于潜移默化间培养学生的逆向思维能力，从而灵活应对各类题目.

一、逆向思维概述

逆向思维，又名求异思维.顾名思义，是与正向思维相对立的概念，指的是针对某一具体问题，选择从反方向寻找思维的突破口，进而找到解决问题的方法或者发现事物本质的思维方式.从表面上看，逆向思维打破了惯性思维，以一种非常规的方式分析问题，似乎比正向思维更难以掌握和理解.但事实上，逆向思维恰恰可以简化问题、激发学生创新创造能力，并帮助他们突破解题瓶颈，为学生攻克难题提供了另一条路径.

二、逆向思维能力培养之可行与必行

（一）学情分析

初中生无论在生理上还是心理上都已经具备了接受更高难度知识的能力.初中生的各项生理机能已基本发育成熟，且脑部“边缘系统”在此阶段也最为活跃，具有极高的可塑性.在实际的教学过程中，教师会发现单纯教授学生基础知识是远远不够的，更重要的在于利用科学的方法将理论与实践、知识与题目融合起来，如此才能应对日趋灵活的数学知识运用.因此，逆向思维能力的培养便尤为重要.于学生而言，形成逆向思维不仅意味着以往的学习方法得到了更新和优化，而且有助于开发脑部智力，拓宽创新思路，从而进一步巩固强化所学知识.一方面，学生遇到高难度问题时不再局限于一种解题思路，能够发现解决问题的突破口，进行反向推理，找到全新且有效的解题模式，大大提升学习效率.另一方面，学生在初步掌握数学公式及定理时，也可以从反向推导的角度寻找定理与定理、公式与公式之间的某种逻辑联系，强化自身记忆，为接下来的题目解答奠定扎实稳固的理论基础.

（二）教情分析

事实上，学生的逆向思维能力培养并非在初中阶段才备受关注.自义务教育伊始，大部分学生就已经掌握了“答案检验”这一能力，即在初步得到答案后从所得答案入手，逆向推导验证题目，若双向证明都成立，便可以验证为正确答案，这是较为初级的逆向思维的运用.而随着学龄段的提升，逆向思维的表现形式也发生了变化，初中数学教材中定理、公式内容占比较大，且大部分知识都带有双向性的特征，例如勾股定理及其逆定理，几何分析题目中的“反证法”“反比例函数”等，都鲜明地体现出正向思维与逆向思维之间的相关性.由此可见，逆向思维运用在数学教学中有着悠久的根源，潜移默化地影响着不同阶段学生的思维能力，为激发学生的创新能力创造条件.

从长远来看，逆向思维在数学教学中的渗透只会日趋增多，显示出培养学生逆向思维能力的必行性.初高中数学知识之间的显著差别之一便是由抽象变得更加抽象，例如初中数学在函数知识方面主要介绍一些基本概念和运算，如简单的一次函数、二次函数等.而高中数学教材中则包含了更多的函数内容，如幂函数、指数函数、对数函数等.这些函数在定义域、值域、单调性等方面有很大差异.显而易见，高中知识深度和广度都进一步提升，为应对这一变化，学生在初中阶段就应及时打好思维基础，熟练掌握运用逆向思维解决问题的方法，为迎接未来挑战夯实基础.

（三）课标分析

《义务教育数学课程标准（2022年版）》（简称“新课标”）中对于培养学生数学核心素养的要求有三点，即用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界.这三点紧紧围绕着“现实世界”从眼光、思维、语言的角度阐明了新时代数学核心素养要求，而“思维”作为三者之一，建立起了不同数学对象之间、数学与现实世界之间的紧密联系，起着上联下达、沟通前后的重要作用.逆向思维虽然仅是众多思维方式中的一类，但在推理和运算方面的应用与新课标对学生运算能力、推理能力所提出的要求相呼应，涵盖范围广、应用频率高，有助于教师在教学过程中的灵活运用，使其贯穿课堂始终，显示出逆向思维能力培养的现实可行性.

三、培养学生逆向思维能力的策略

（一）反向推导理论，夯实知识基础

初中数学涉及的计算与推理需要以丰富的理论知识作为基础，正如几何证明题的推导不仅要求学生具备逻辑、判断、推理等各种能力，还需要熟练掌握有关几何证明的理论知识.只有搭建起稳固的理论框架，学生才能够灵活运用各类定理、公式解决实际问题.然而在实际学习过程中，学生又往往难以找到扎实记忆理论知识的方法，记错、记混、遗忘等各类问题层出不穷.究其根本便在于学生常常死记硬背数学定理与公式，很难维持长久记忆，且学生对理论的理解也仅仅停留于表层，未能摸清理论的推导过程，因此出现了基础不扎实问题.对此，教师可以采用反向推理的方式向学生展示相关定理与公式的推导过程，引导学生摸清理论背后的逻辑和规律，并将其融入具体的题目当中，多做多练，不断加深记忆.

以“圆的切线性质定理：圆的切线垂直于过切点的半径”的证明为例.教师可以用反证法对这一定理进行证明，启迪学生学习方法，夯实记忆.具体来说，一条直线l是圆O的切线且切点为A，假设直线l不垂直于OA.若过点O作OM垂直l于点M，则OM等于半徑.因为垂线段最短，所以OA的长度大于OM，即半径大于半径，矛盾，由此可得这一假设并不成立，故直线l与OA垂直，“圆的切线垂直于过切点的半径”得证.

（二）突破常规思维，创新题解思路

又如下题：

在△ABC中，∠B=45°，D为BC上一点，DC=2BD，且∠ADC=60°，求∠C的度数.

首先教师应先根据已知条件画出较为精确的草图（如右图），将文字转化为直观的几何图形，并把能够直接推导出来的角度、边长等信息添加到图形中，比如根据“三角形的外角等于与它不相邻的两个内角的和”可得出∠BAD=15°.但在准备工作完成后便会发现以现有的已知条件很难直接推导出∠C的度数.在正向思维受阻的情况下，教师可以启发学生转换思路自己创造条件，利用已知推未知，即过C点作辅助线CE⊥AD于点E，如此便得到了∠DCE=30°.由于新构建出来的△CDE是一个直角三角形，且三个内角的度数分别为90°，60°，30°，所以这一直角三角形的三边比例为1∶3∶2，即DC=2DE，又因为已知DC=2BD，所以BD=DE，此时连接BE，就构建出了一个等腰三角形BDE，由此得出∠EBD=∠BED=30°，所以∠ABE=15°，再加上之前推算出的∠BAD=15°就可以发现△ABE同样是一个等腰三角形，所以BE=AE.又因为∠EBC=∠ECB=30°，所以△BEC也是等腰三角形，且BE=EC，综合起来便可得知BE=EC=AE，△AEC是等腰三角形，所以∠EAC=∠ACE=45°，则∠ACB=30°+45°=75°.

（三）设置开放性问题，打破思维桎梏

数学知识源于现实生活，并以解决实际问题为最终目标，体现在教学之中便产生了开放性较强的数学应用类题目.所谓的“开放性”并非一定没有准确、唯一的答案，而是解决同一问题的思路可以多种多样，这就为开拓学生思维提供了良好的机会.因此，为更高效地培养学生的逆向思维能力，教师可以从开放性问题着手，引导学生探索不同的解题思路，打破思维桎梏.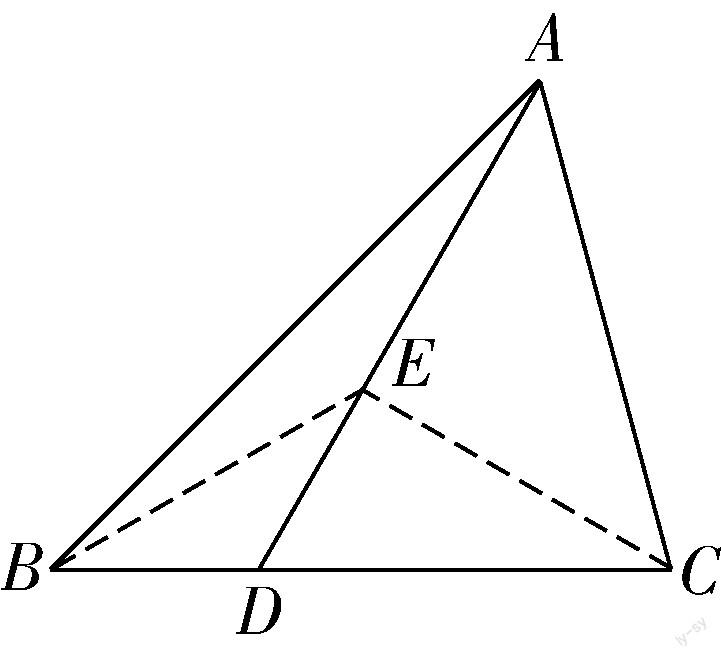

以“解一元一次方程”为例：某公司连续三年一共购买28台打印机，第二年购买打印机的数量是第一年的2倍，第三年购买的数量又是第二年的2倍，则该公司第一年购买的打印机数量是多少？

结 语

综上所述，逆向思维能力的培养为学生核心素养的提升提供了更多可能.学生在掌握逆向思考方法后不仅能使思维更加灵动，设想更多解题的可能性，还可以利用它快速检验自己所得结论的正确与否，养成检查的良好做题习惯.于教师而言，合理选择教学方法，在教学过程中灵活融入逆向思维能力培养，为学生示范解题思路有助于改善学生的思维习惯、提升其创新能力.因此，无论是课堂教学还是家庭作业，教师都应为逆向推理训练留有一席之地，在潜移默化中培养学生的创新思维能力.

【参考文献】

[1]魏全定.培养思维，鼓励创新———初中数学教学中学生思维能力的培养[J].山西教育（教学），2022（12）：81-82.

[2]朱倩芸.初中数学教学中学生逆向思维能力的培养策略[J].天津教育，2022（33）：49-51.

[3]李文江.浅谈初中数学教学中学生逆向思维能力的培养[J].试题与研究，2022（31）：4-6.

[4]吴辉集.初中数学教学中学生逆向思维能力的培养[J].亚太教育，2022（20）：149-151.

[5]張海燕.初中数学教学中学生思维能力的培养路径探索[J].数学学习与研究，2022（25）：26-28.