全电子安全系统侵彻过载特性与通带算法研究

杜廷蔚，张祥金，郭竞杰

(南京理工大学 机械工程学院， 南京 210094)

1 引言

全电子安全系统(ESAD)的直列式、钝感引爆等特性，使得ESAD具有较高的安全性、可靠性、可交互性。目前ESAD主要由前端制导系统给出的制导信号进行信号识别和处理，但应用于侵彻武器时，前端系统在高过载工况下失效率往往较高，因此在ESAD中加入信号采集与处理模块作为冗余系统是必要的，对于ESAD在侵彻弹药中的应用具有重大意义。

孙倩华等[1]针对过载信号粘连,提出了基于盒差分滤波的侵彻引信计层信号预处理方法。黄莎玲等[2]在融合信号计层算法基础上提出一种自适应阈值层目标识别算法。房安琪等[3]提出基于数据增强的侵彻引信准确层识别神经网络方法。王燕等[4]采用时频分析法研究弹体主轴方向加速度信号的Choi-Williams能量分布特征，提出以侵彻过程加速度信号的能量分布为依据的层识别方法。以上文献对单片机性能要求高，难以应用于实时工况中。李豪杰等[5]采用将弹体与引信分离建模获得引信部位侵彻过靶的加速度信号，提出采用弹丸识别入靶过载信号后短时屏蔽计层功能的方法。

以上文献都涉及对过载信号的滤波处理，但却仅凭经验设计了低通滤波的截止频率，往往并不准确。本研究中利用对ESAD仿真得到的动态响应信号提出了一种通带算法，并根据此截止频率设计了低通滤波器，通过了半实物仿真验证。

2 ESAD组成与侵彻仿真

ESAD主要模块如图1所示，信号采集与处理模块实现弹丸侵彻靶板过程中ESAD的过载信号采集与处理，输出的触发信号输入低压控制模块，低压控制模块主要接收前端制导单元和信号采集与处理模块输出的环境触发信号与高压生成模块输出的反馈信号，实现发火信号的控制和高压生成模块的电压，起爆模块用于接收发火信号，并起爆爆炸箔，引爆战斗部，实现弹丸精准起爆控制。

图1 ESAD模块框图

ESAD中信号处理单元框图如图2所示，MEMS传感器采集弹丸侵彻靶板过程中ESAD的动态响应信号，通过信号放大器与高通滤波器，再由AD转换器将响应信号输入控制处理单元中，实现对弹丸穿靶的检测，达到精确计层的目的。

图2 信号采集与处理模块框图

如图3所示，根据实际侵彻弹丸、ESAD和混凝土靶板结构，建立1/4数值仿真模型，因为弹体内部包含了各种材料和机械结构，使得对ESAD这一特定部分进行动态响应分析非常困难，因此本文将除ESAD外的整个弹体做均匀介质整体考虑。同时弹丸中⑤部分为ESAD，根据应力波衰减理论[6-7]，当峰值很高的应力波从波阻抗很低的材料向波阻抗很高的材料传递时，幅值会大幅降低，因此，为降低ESAD内部应力，提高抗冲击能力，并固定内部芯片及引脚，在ESAD内部用波阻抗低的环氧树脂⑥进行灌封[8-9]。此外，本研究中忽略了MEMS加速度传感器自身的扰动。

图3 侵彻弹丸、ESAD和混凝土靶板仿真模型

本仿真对ESAD、弹体与混凝土中弹靶作用区域进行了网格加密处理如图4所示，采取Lagrange显式动力学算法，弹体与ESAD外壳采用钨合金Johnson-cook本构模型和Mie-Gruneisen状态方程[10-11]，混凝土采用Rht本构模型与p-α状态方程[12-13]，关键参数如表1所示[14-15]。

图4 网格划分示意图

弹丸质量为40 kg，口径为100 mm，长度为300 mm，初始速度设置为680 m/s，初始时刻弹头距离靶板50 mm，混凝土靶厚设置为100 mm，靶板间隔设置为500 mm，过载值测试点选取为ESAD内部如图5所示。图6为用Matlab输出的环氧树脂灌封后的ESAD过载加速度信号，从其中可以看到ESAD过载信号极其不稳定，主要是因为弹丸在穿靶过程中，真实的过载信号与弹体中的高频振动信号产生了混叠，使得过载响应在时域上存在层与层之间的粘连现象，需要的过层信号被杂波信号淹没，ESAD难以判断真实的过层信号。ESAD穿靶的速度变化如图7所示。

图5 加速度测试点

图6 灌封后ESAD过载加速度波形

ESAD位移如图8所示，ESAD在整个侵彻过程中没有发生与弹体的相对位移，可以通过ESAD的位移距离来判断弹丸撞击靶板的时间窗如表2所示。

图8 ESAD位移变化曲线

表2 弹丸穿靶时间窗

ESAD中真实的过载响应信号频率非常低，理想情况下的频率为

(1)

式中:v为ESAD穿靶的平均速度；l1与l2分别为弹丸长度与靶板厚度。根据ESAD速度响应曲线可以计算出ESAD过载信号的理想频率f0是1.7 kHz。

3 低通滤波器通带算法研究

低通滤波器截止频率选择对过载信号有决定性的作用，信号中通带外的频率会受到极大地衰减，若ESAD真实过载信号处于通带外，那么后端信号处理单元就无法正常工作，会导致弹药的误炸甚至不炸。因此通带的选取尤为重要。

滤波后的信号可能存在2种情况，一是截止频率选择过小，原本真实的过载信号被滤除，余下信号为低频杂波信号；二是截止频率选择得过大，余下信号还存在多余高频杂波[16]。本文针对这2种情况提出了一种通带选择算法，算法流程如图9所示，其中初始截止频率采用理想截止频率f0计算，经过每层靶板的计算速度变化值vc与实际速度变化值vi的比较需要执行4次，以降低误差。

图9 通带算法流程

考虑到加速度值a的解析解比较复杂且精度不高，本文采用复化梯形数值积分的方法来计算近似积分值，其算法为

(2)

式中：vc为计算的速度变化值；t1与t2分别为弹丸入靶和出靶的瞬时时间；h=(t2-t1)/n为数值积分计算的步长；a(t1)为ESAD在t1时刻的加速度；a(t2)为ESAD在t2时刻的加速度；n为对数值积分做等分点的个数。

实际上，加速度a在下限为t1与上限为t2的定积分值为：

(3)

式中：ti=t1+ih；i=0,1,…,n；n→+∞。

根据Lagrange插值多项式的截断误差，可以得到，在[ti,ti+1]区间内，有：

(4)

式中：a″(ξi)表示加速度在点ξi的二阶导数，其中ξi∈[ti,ti+1]。

将式(4)代入式(3)并与式(2)求差值，可以得到复化梯形数值积分的截断误差：

(5)

根据式(5)可以看出，截断误差En(a)以1/n2的速度衰减，当n→+∞时，En(a)=0。在算法中，控制截断误差及数值积分得到的速度误差控制在0.000 1，将算法通过Matlab实现，滤波后可以得到ESAD经过每层靶板的速度变化值。

因为弹体内应力波传播时间问题会导致ESAD接收到过载信号会比弹丸撞击靶板的时间晚，因此此次计算将弹丸撞击靶板的时间窗往后移动30 μs。根据前文所述弹丸穿靶时间窗，列出弹丸实际速度变化值，因为本文只研究ESAD在正侵彻方向上的加速度值，因此也只关注ESAD在正侵彻方向上的速度值，如表3所示。

表3 实际ESAD速度变化值Table 3 Actual ESAD speed variation value

将滤波后计算得到的速度值精度控制在5%以内。

(6)

根据算法可以计算得到截止频率f0=1 965 Hz，速度误差如表4所示。

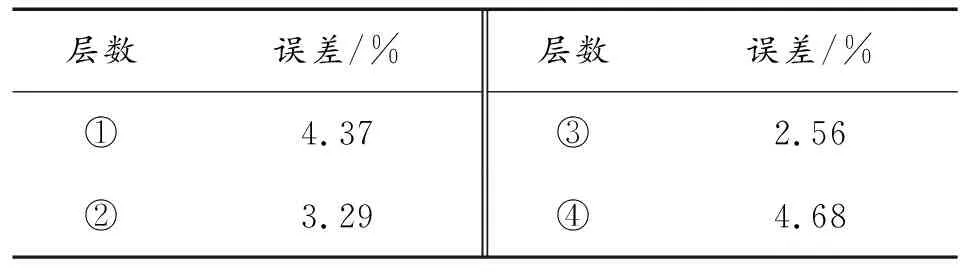
表4 速度误差Table 4 Velocity error

由表4可以看到，计算得到截止频率对应的速度误差较小。滤波曲线如图10所示，可以看到滤波后曲线可以明显的分辨出过载信号和粘连信号，但信号中仍然存在一部分噪音，只需要在后续软件中采用阈值加时间窗的方法来实现计层，证明了此算法计算出的截止频率的有效性。

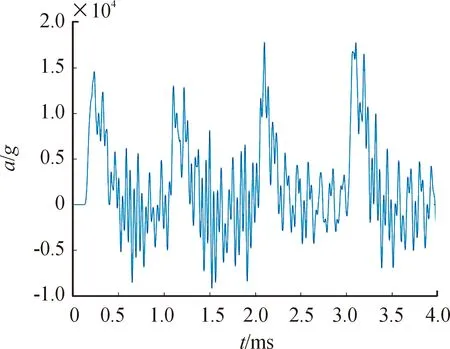
图10 侵彻4层靶板ESAD过载滤波曲线

4 半实物仿真用滤波器原理及设计

有源滤波器相较于无源滤波器无电感满足ESAD的小体积约束，且对ESAD内部如高压电容、MCT等对电磁兼容性要求高的元器件产生的干扰小。本文根据ESAD动态响应特征基于Sallen-key典型电路设计了一个低通模拟有源滤波器。

4.1 Sallen-key典型电路

Sallen-key(SK)是有源滤波器设计的一种拓扑结构，VCVS(Voltage-controlled voltage-source)滤波器的变种，由麻省理工学院林肯实验室的R.P.Sallen和E.L.Key在1955年提出[17]，此拓扑具备输入阻抗高、电路结构简单、Q值和通带增益受元件参数的影响小、品质因素调节方便且可调范围大、易于实现增益的精确设计等特点，在军事装备领域得到了广泛的应用[18]。其基本结构如图11所示，Z1、Z2、Z3、Z4以阻抗形式表示。

图11 Sallen-key拓扑结构

根据理想运放虚短、虚断概念可以得到：

(7)

式中：UO为输出电压；UP和UN分别是运放的正负输入端。在U1点运用KCL与虚断原理可以得到：

(8)

将式(7)与式(8)联立可以得到传递函数：

(9)

4.2 基于Sallen-key的低通滤波器设计

根据SK拓扑结构，将Z1、Z2选作电阻对应R1、R2，Z3、Z4选作电容元件C1、C2，如图12所示。将电容与电阻阻抗表达式代入式(9)中，可以得到SK低通滤波器的传递函数，如式(10)所示。

(10)

低通滤波器二阶响应标准形式：

(11)

图12 SK低通滤波器

对比式(10)和式(11)可以得到此低通滤波器的截止角频率如式(12)所示和品质因素如式(13)所示。

(12)

(13)

滤波器的品质因素Q>0.707时，滤波器频响会在截止频率处出现峰值化，而Q<0.707时，响应曲线过渡会趋向平缓，选择Q值为0.4。截止频率f0在通过前文算法得到为1 965 Hz，因此截止角频率w0=2πf=12 346 rad/s。将Q值代入式(13)可以得到

(14)

结合实际，选择C1=2.2 nF，C2=4.4 nF，R1=R2=26 kΩ，通过计算可以得到截止频率f0=1 967 Hz，Q=0.4，其Bode图如图13所示。

图13 SK滤波器Bode图

从图13可以看到，此滤波器对于低频段的信号衰减幅度较小，-3 dB处的频率为1 970 Hz接近1 967 Hz，过载波形滤波仿真后结果如图14所示，满足第2节中提到的特定截止频率的滤波器要求。

图14 SK滤波器仿真图

滤波器截止频率与设计的截止频率有误差，将滤波器输出的响应信号代入式(2)，可以得到对应的穿靶速度误差如表5所示。

表5 滤波器响应信号误差Table 5 Filter response signal error

从表5中可以看到，过靶速度变化误差控制在了较小的范围，满足工程设计要求。

5 半实物仿真实验验证

由于实验条件所限，采用ESAD半实物仿真系统对信号采集模块进行验证。ESAD半实物仿真系统由电源、波形发生器、ESAD、示波器组成。波形发生器用于将以往试验中采集到的加速度数据转化为模拟电压信号，输入ESAD中的信号采集模块中以代替加速度传感器输出信号，信号采集模块中低通滤波器的响应波形直接输出至示波器中。图15所示为弹丸侵彻3层靶板的试验数据。

图15 侵彻3层靶板ESAD过载值

在第1节仿真中为了节省仿真时间，在仿真计算中缩短了靶板之间的距离，但仿真计算时所用模型与试验所用弹丸与靶板模型一样。直接运用3节设计的滤波器对试验数据进行滤波，结果如图16所示。图中可以看到，低通滤波器对试验过载信号的响应曲线分层信号清晰，结合阈值加时间窗算法可正确计层。

图16 滤波后的过载信号

6 结论

1) 在弹丸侵彻目标时，ESAD过载响应曲线复杂多变，需采用具有精确通频带的低通滤波器。

2) 本文提出的通带算法直接通过前期仿真计算获得，不需要单片机实时计算复杂算法，提高了模块的实时性。

3) 通过本文算法得到的截止频率通过半仿真实验验证，结果表明其具有较好的分层特性，结合后端阈值加时间窗算法可以有效识别弹丸穿靶。