保持几何特征的导弹发射车模型简化算法

姜艺诺，王 伟，田 泽

(1.西安工程大学 计算机科学学院， 西安 710048； 2.集成电路与微系统设计航空科技重点实验室，西安 710068)

1 引言

随着计算机科学技术及数字媒体的发展，三维模型精确度得以提高。在一些3D仿真应用场景中，如军事模拟作战、导弹发射追踪，这些复杂场景的构建可能需要数万个三角形网络，复杂的模型给计算机的存储、传输、渲染过程带来了巨大的挑战。同样，由于导弹发射车模型存在大量的三角面片，导致仿真应用场景中模型加载不流畅、渲染时间过长，从而直接影响系统性能[1]。在保证模型特征的情况下，较低内存的占用、快速的数字传输和高效的物理计算是首选和必要的，因此需要相对简单的模型代替原有模型。自20世纪70年代初，国内外学者提出了许多网格模型简化算法，目前一般可分为4类：顶点聚类法[2]；顶点删除法[3]；边折叠法[4-6]；三角形折叠法[8-9]。其中，顶点聚类法是将三维模型划分为一定数量的子空间，简化后的子空间顶点聚类都会被新顶点代替，之后再删除与原顶点相关联的三角形面片或者重叠的边，该算法计算速度较快，但对面积较大的平面简化程度较低，同时会造成模型细节特征丢失的现象，生成模型质量不高。顶点删除法通过迭代方式删除网格中小于阈值的顶点进行简化，该方法简单高效，但简化过程需要重新三角化，使模型表面过于粗糙。

边折叠算法首先由Hoppe[4]提出，该算法是一种针对任意二维流形的三角形网格模型简化方法，是一个全局能量函数的非线性优化，它需要大量的计算以及长时间的运行，执行效率较低。1997年，针对Hoppe算法存在的缺点，Galand提出一种基于二次误差度量(quadric error metrics，QEM)的边折叠算法[5]，利用局部二次误差度量的方法来计算边缘折叠的误差，将新顶点到与该点相邻的平面的距离的平方作为度量误差，该算法计算简单，运行速度较快。杨晓东等[6]在边折叠的基础上引入局部面积度量的方法来改变模型特征和平坦区域上顶点折叠的次序，更好的突出了模型的特点。Sadia Tariq等[7]在边折叠的基础上，通过简化同一模型多个副本文件加快算法运行时间，并将顶点纹理信息加入误差矩阵中，提高了模型的简化质量。

三角形折叠算法和边折叠算法的思想大致相同，Zhou 等[8]首先计算出折叠点到相邻曲面距离的平方和，按照最小化折叠代价顺序对三角形折叠实现模型简化，由于算法以三角形折叠为中心，在简化率相同的情况下，其折叠速度明显优于边折叠。车力等[9]将三角形折叠与多视觉感知相结合并借此定义三角形折叠误差度量函数，可以很好地保持算法的边界特征，并有效改善模型质量，但由于多次计算不同视点误差造成算法耗时较长。

比较上述几种折叠算法，三角形折叠算法具有几何意义较为直观、算法效率较高等特点。为了解决QEM简化算法会造成模型几何特征丢失的缺点，提出保持几何特征的三角形折叠(triangle collapse preserving geometric features，TCPGF)算法，将三角形折叠引入到QEM算法中，并加入体积比及网格显著度因子来构建几何特征误差度量函数，在保持模型简化时间差别不大的前提下进一步提升模型质量，较好的保证模型的原始特征。

2 二次误差度量算法与三角形折叠

给初始模型中任意一个三角形Ti设置一个4×4的误差矩阵Kp，v为模型的任意顶点，包含顶点v的三角形集合用Ci表示。设一个平面p的方程表示为ax+by+cz+d=0，其中a、b、c、d为常数，不同时为0。然后，将该平面缩写为p=[a,b,c,d]T，且a2+b2+c2=1。则顶点v=(x,y,z,1)T到Ci的平方和为：

(1)

根据平面p=[a,b,c,d]T可知，每个三角形平面可以计算出大小为4×4的对称矩阵Kp，如式(2)所示：

(2)

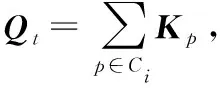
(3)

QEM算法旨在使新折叠点引起的折叠误差尽可能小。因此，计算该方程(3)中偏导数，并将其设为0。由此得到了一个线性方程如(4)所示：

(4)

解得：

(5)

若方程(4)可以求解，而且方程左侧的矩阵是可逆的，则从方程中可以得到新折叠点的位置，如式(5)所示。若不可逆，则将三角形的重心作为新的折叠点。三角形折叠法如图1所示。

QEM算法简化的几何基本元素是三角形，其累加性较好，本文中将边折叠延伸为三角形折叠，并更新折叠代价：

(6)

由于QEM算法没有考虑模型局部形态，测度标准过于单一，基于以上原因，为了使简化后的模型准确表达出原始模型的特征，下文将引入体积比和网格显著度，并将两者统称为约束因子，给出了一种类似于QEM的误差标准，能够有效地控制三角形的简化顺序。

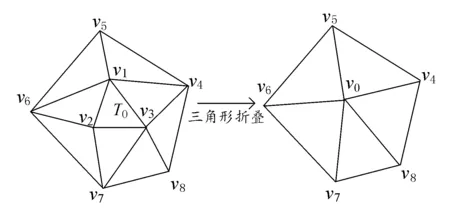
图1 三角形折叠法

3 约束因子的构建

3.1 体积比

体积作为一种常见的误差函数控制变量，旨在从几何尺度方面尽可能逼近原始模型[10-11]。本文中体积比指模型中三角形与原点围成的体积在简化前后的比值，并用该值来量化模型简化前后模型体积变化情况。

定义常见的三角形网络T，T=(t1,t2,t3,…,tn)，其顶点集合为V，V=(v1,v2,v2,…,vi)，与三角形3个顶点邻接的三角形被称为邻域三角形，如图2所示。被折叠的△v1v2v3三个顶点坐标分别为v1(x1,y1,z1)、v2(x2,y2,z2)和v3(x3,y3,z3)，由定义可知其邻域三角形为△v1v6v2，△v1v5v6，△v1v5v4，△v1v3v4，△v2v6v7，△v2v7v3，△v3v7v8，△v3v4v8。

图2 三角折叠引起的体积变化

设A为三角形的顶点坐标矩阵，|A|为对应坐标矩阵的行列式，则△v1v2v3与原点所围成的四面体的体积可由式(7)计算：

(7)

若初始网格中顶点v邻域三角形个数为m，则邻域各三角形顶点坐标矩阵为Ai(k=1,2,3,…,m)。△v1v2v3折叠后生成的顶点为v0后，设折叠后顶点v0的邻域三角形个数为n，同理每个邻域三角形坐标矩阵记为Bi(k=1,2,3,…,n)。则删除点v后模型体积比(volumetric ratio，VR)由式(8)计算:

(8)

为了使简化后的模型保持原有特征，仅仅依靠体积比来约束误差函数是不够的，对于模型简化来讲，网格的细节特征也是需要考虑的重要因素之一，下面将对误差函数加新的约束条件，合理化目标函数。

3.2 网格显著度

从视觉方面来讲，二维图像的显著度是指图像上能够吸引观看者兴趣、捕捉到注意力的某些特征，一般包括图像的纹理、颜色、亮度等信息，并且可以量化出来。而在三维模型中，网格显著度一般基于网格特征计算，比较常见的有高斯曲率、主曲率、平均测地线距离等等[12]。Lee等[13]首先提出了计算机图形学中网格显著度的概念，将图像中的显著度引入到三维网格中。

为了提取网格显著度，需要对网格噪声进行处理，因此滤波算法的选取极为重要。本文中使用双边滤波来计算网格显著度。双边滤波是一种线性的过滤方法，与高斯滤波相比，双边滤波将像素值相似度和空间邻近度进行一种折衷处理，以像素为单位进行操作，可以在达到滤波效果的同时，保证图像边缘结构[14]。双边滤波器公式化描述如下：

(9)

(10)

式中：c(ξ,x)为空间距离相似度高斯权重；s(f(ξ),f(x))为像素相似度高斯权重；k(x)用来对双边滤波结果单位化。

由于高斯曲率和平均曲率对特定曲面敏感度不足，为了准确反应网格面几何属性，本文中的像素值不采用平均曲率代替，而使用周继来等[15]的方法，使用顶点曲度代替。网格显著度计算步骤如下：

1) 计算三维网格的顶点曲度:

(11)

式中：KG为顶点的高斯曲率;KH为顶点的平均曲率，两者均通过文献[16]中计算方法求得。

2) 计算基于三维网格顶点曲度的双滤波空间距离权重αc以及特征保持度权重βs：

(12)

(13)

3) 计算三角形网格显著度值：

(14)

(15)

式中：P为顶点的一层邻域；C(x)为顶点曲度。根据大量实验，取σdist为v一阶邻域内三角形边长的平均值，图3为导弹发射车组件网格显著度图像，根据图像可知，模型中的颜色较深部位代表网格显著度较高的区域，同时也说明该区域模型几何特征较明显。颜色较浅代表显著度较低的部位，该区域网格变化较为平缓，特征度相对较低。

图3 组件一、二网格显著度图像

4 TCPGF算法

导弹发射车模型结构复杂，建模精度较高，部件连接复杂。针对以上特点，在QEM算法基础上加入体积比以及网格显著度这两个约束因子建立新的折叠误差函数。由于TCPGF算法是根据三角形的折叠代价大小进行三角形折叠操作的，故如何计算折叠代价，直接影响到折叠三角形的选择以及新顶点的确定。

4.1 折叠代价的计算

将体积比VR(Ti)以及网格显著度约束因子B(Ti)作为参数添加到式(6)中进行新折叠误差的计算。三角形T0折叠后引起的局部体积比值越高，显著度越高，表示该网格局域属于特征明显区域，则应延迟折叠该区域三角形，更新折叠误差矩阵如下所示：

Qt′=(VR(Ti) +B(Ti))Qt

(16)

式中：VR(Ti)与B(Ti)分别根据式(7)—(15)求得。那么新的折叠误差标准为：

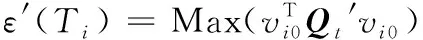
(17)

4.2 新顶点的确定

(18)

vi0即是三角形折叠的最佳位置。若该方程无解，则将三角形的重心作为新顶点的位置，如图4所示，重心即三角形三条中线的交点，是三角形最佳平衡点，坐标根据三角形3个顶点坐标的几何均值求得，即：

vi0=(v1+v2+v3)/3

(19)

图4 三角形重心

4.3 算法步骤

本文中提出的基于三角形折叠的网格简化方法采用堆排序的方法按照折叠误差的大小进行排序，模型特征越明显的部位网格显著度越高，折叠后引起的体积变化较大，因此每次简化就要延迟该三角形的折叠，即每次在堆中提取误差最小的三角形进行简化。

步骤3：计算每一个三角形的折叠误差，并按照折叠误差从小到大排列三角形，将其加入误差堆队列中；

步骤4：将折叠误差最小的三角形从队列中取出并折叠，更更新所有相关信息，若折叠误差为0，则将其插入到误差为零的三角形队列后；

步骤5：若达到需求的简化率或者队列为零，则转到步骤6，否则转到步骤4；

步骤6：算法终止。

4.4 算法合理性分析

文中提出的保持几何特征约束算法在设计过程中采用QEM进行三角形折叠方法，一次可以同时简化2个三角形，相当于两次边折叠的效果，具有更快的迭代速度。但仍然存在简化后网格过于均匀的缺点，故引入了体积比以及网格显著度两个参数，与二次误差度量方法结合，合理维持局部网格形状变化，弥补了经典QEM算法无法保持模型细节、简化网格过于均匀等缺点，使算法在时间开销与现存算法差别较小的前提下向优化的方向发展。QEM算法是公认简化效果好、适用性高的算法，将仿真结果与QEM算法(文献[5])和在其基础上改进的算法(文献[6])进行对比，保证了该算法的合理性与可行性。

5 实验结果及分析

所有实验在处理器为Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz 1.99 GHz、操作系统为Window 10、安装内存为8 GB的计算机平台上，通过Visual Studio平台上实现。导弹发射车三维模型数据来源于集成电路与微系统设计航空科技重点实验室(1)集成电路与微系统设计航空科技重点实验室设立于2015年，主要研究方向包括：智能计算机基础理论、新型机载网络理论及芯片设计技术，积累了大量实验设备、关键技术，是航空领域核心集成电路前沿阵地以及人才培养和专业发展的综合平台。，由3DMAX软件制作，将其导出为.obj文件并在此基础上进行实验。

为了验证改进算法的合理性，实验采用多种距离误差以及算法时间开销作为指标，与文献[5-6]中模型简化算法对比。

5.1 不同简化率下模型简化效果对比

由于导弹发射车模型数据量太大，实验针对性选取了导弹发射车两个特征明显的部件作为仿真实验对象。如图5所示的组件一(a)，组件二(b)。其原始模型分别含有1 674与4 004个三角形面片，其中组件一模型表面顶点分布较为均匀而且是连续的表面；而组件二几何特征复杂，顶点分布不均匀且模型表面不连续。

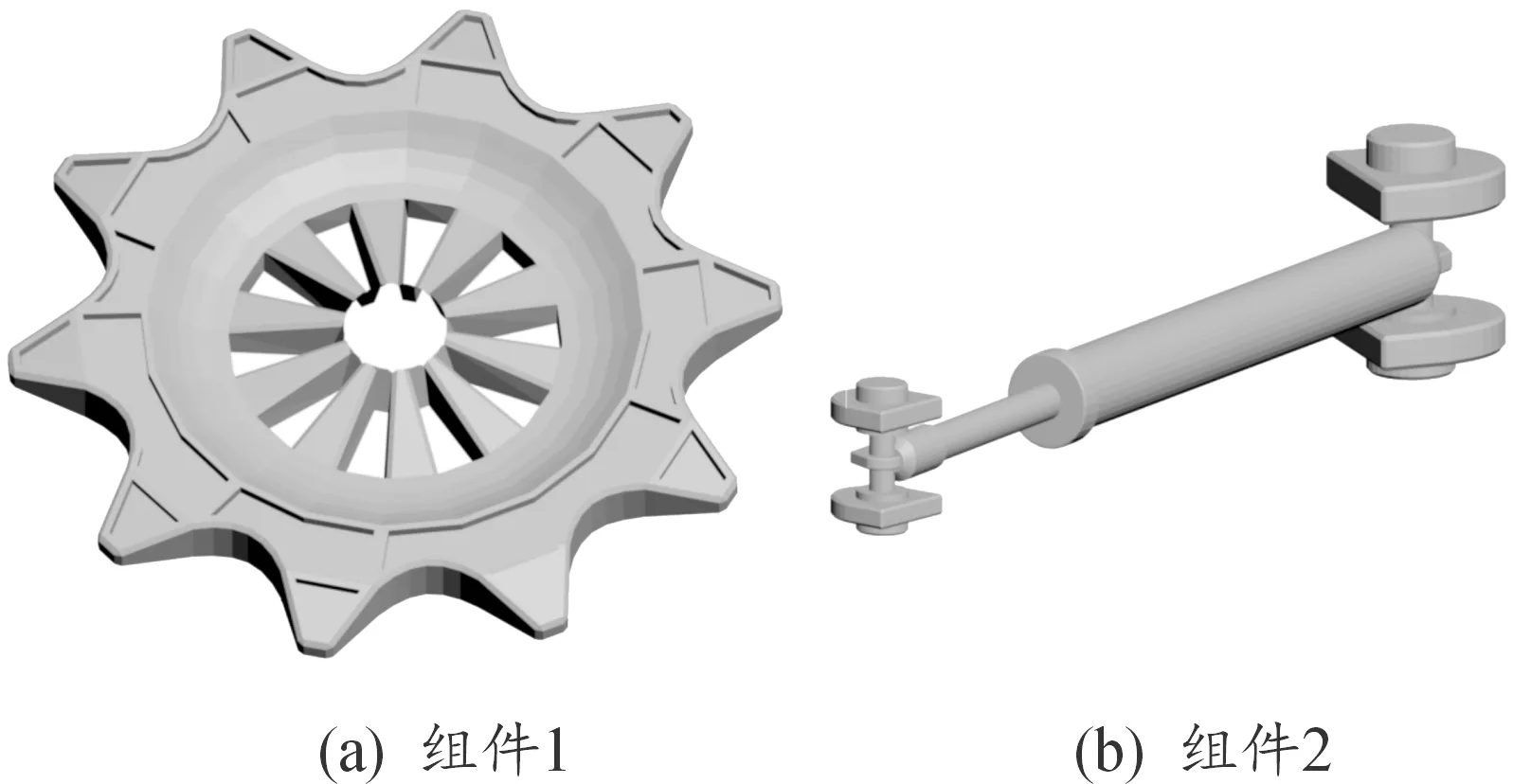
图5 组件一、组件二原始模型图

为验证改进模型简化算法效果，图6中(a)—(c)是使用文献[5]算法、文献[6]算法以及本文算法对组件一简化15%的简化结果，可以看出三者在视觉效果上没有明显差异。直到将模型简化率提高至85%时，如图6(g)—(i)所示。文献[5]算法简化后的模型虽然边角特征未退化，但三角网格分布过于均匀，与原模型差别较大。采用文献[6]算法后模型梯形边角退化为尖锐的三角形，无法保持模型原始特征。相比较看，本文算法可以有效防止模型边角特征退化。

图6 组件一模型简化结果对比

图7给出了组件二分别采用文献[5-6]和本文算法在简化率15%、55%、85%下实验简化结果，由于组件二顶点数比较多，使用3种算法将模型简化15%时，如图7(a)—(c)所示，很难从视觉方面比较的简化效果。

图7 组件二模型简化结果对比

当简化率提升至85% 时，使用本文算法简化的模型轴体区域保存仍然比较完整，轴杆头尾特征明显，没有出现较大范围的特征退化，使特征能够较好的保留下来，并且网格显著度高的区域较稠密，而使用文献[5-6]对模型同样简化85% 时，轴体左端部位形变率较大，而且网格显著度较低的区域网格仍较稠密。由此可见，加入体积比以及网格显著度2种约束因子能够有效地保持原始模型特征。

图8为简化率为85% 时局部细节放大图(图7圆圈标识部位)。从图中更能看出在分别使用文献[5]算法以及文献[6]算法后，组件二模型轴体两端特征已退化，并产生较多的狭长三角形，而本文算法简化结果无较多狭长三角形，也不会造成模型特征退化的现象。

图8 简化率85%时组件二局部对比

5.2 几何误差分析比较

TCPGF算法在保证误差最小的原则下进行实验，为了更好地衡量该算法的优劣性，首先定量分析组件一、二在简化率为15%、25%、35%、45%、55%、65%、75%、85%下的 Hausdorff 距离误差；再通过误差比较工具Metro(v4.07)测量模型简化率为15%和85%时的最大误差和平均误差，根据实验结果验证本文算法性能。

定义Hausdorff 距离为：

Dist(A,B)=max{min{d(pA,pB)}}

(20)

其中，d(pA,pB)为点pA与点pB之间的距离。

图9和图10给出了文献[5]算法、文献[6]算法以及本文算法的Hausdorff距离误差对比结果。由图9、图10可知，当简化程度相同时，使用本文算法得到的组件一的Hausdorff距离误差比文献[5]算法降低了28%～37%，比文献[6]降低了3%～28%；对于组件二模型，使用本文算法简化的几何误差比文献[5]降低13%～30%，比文献[6]算法降低3%～18%，可以看出使用本文算法计算得出的模型误差明显小于其他2种算法，能够更好地逼近原始模型。

Metro误差比较工具由Cignoni[17]等在论文中提出设计，是至今评价误差的主要量化标准，使用Metro测量出的误差对比如表1所示。

图9 不同算法下组件一模型Hausdorff距离误差对比

图10 不同算法下组件二模型Hausdorff距离误差对比

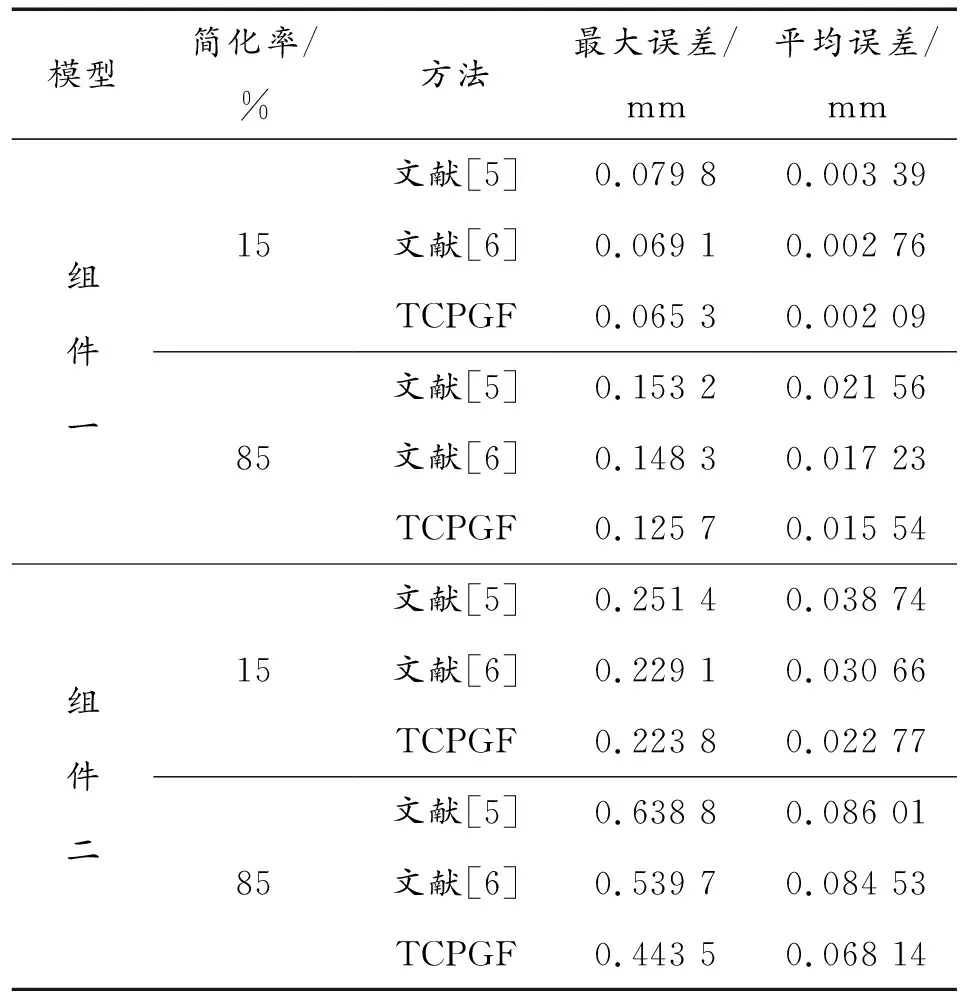
表1 组件一、二简化误差对比

从表1对比数据分析可得，在简化程度较高时，使用本文中方法简化得到的平均误差能够稳定在0.069 mm内，均小于其他算法。随着简化率的升高，计算出的最大误差值与其他2种算法相比差距也变大，这是因为最大误差一般产生在三角形面片密集的区域，而改进的算法在计算简化误差时加入了网格显著度因子，可以有效地控制防止模型显著度较高区域被过度简化，保留了特征点和边，从而较好地保持模型初始特征以及拓扑性。

5.3 时间开销分析比较

时间开销是衡量模型简化算法是否高效的重要指标之一，本文挑选组件一、二模型简化率分别为15%、55%、85%时算法所花费的时间作为三组对比实验，实验数据如图11、图12所示。通过数据对比分析，可以得出结论：模型越复杂，其简化耗费时间越多，由于本文算法需要计算体积比以及网格显著度，所以算法耗时增加，但得到的简化模型质量有较大的提高，且算法耗时差距在毫秒级别，故算法增加的时间开销在可接受的范围内。

图11 不同算法下组件一模型简化耗时对比

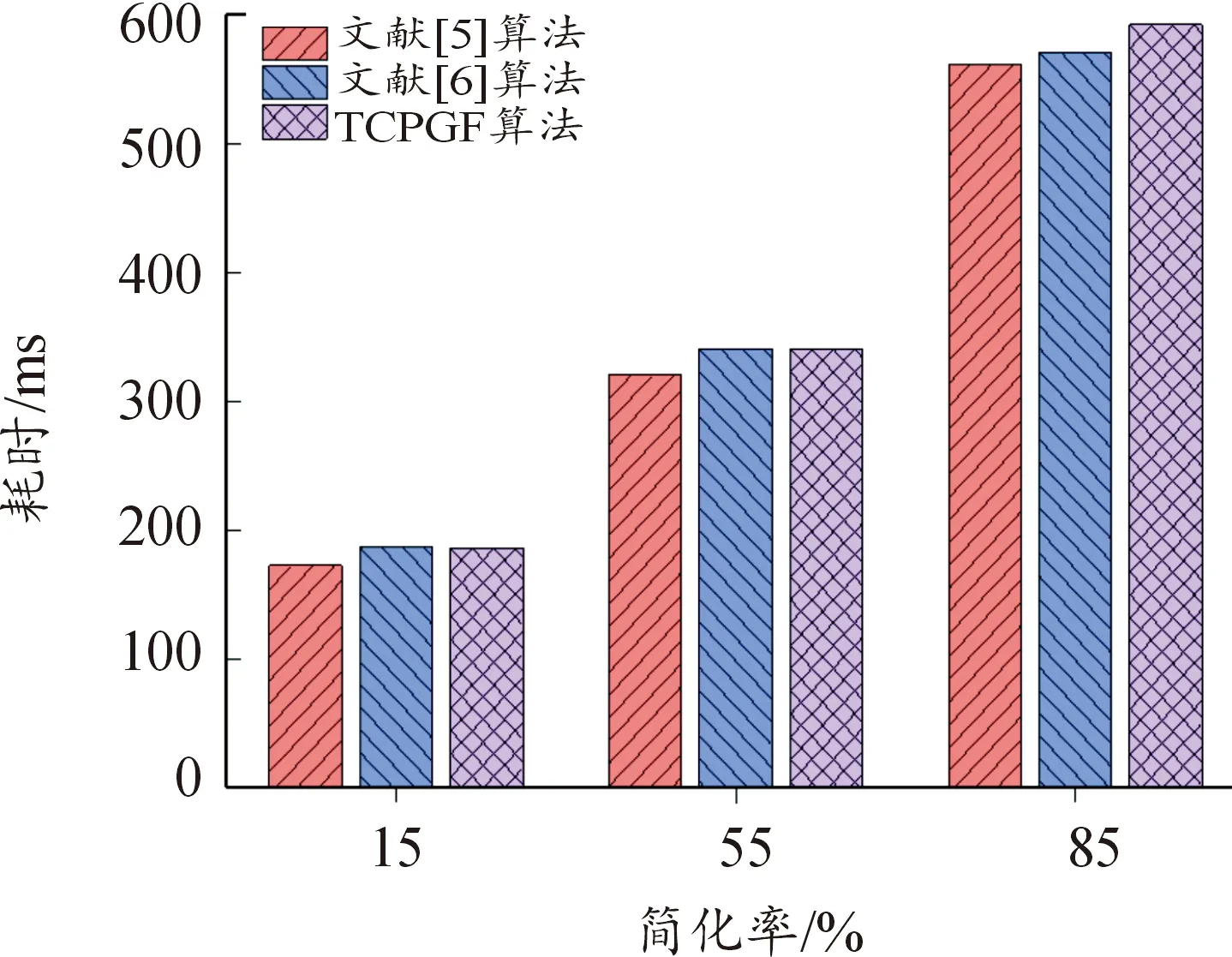
图12 不同算法下组件二模型简化耗时对比

6 结论

提出了一种保持几何特征的导弹发射车模型简化算法，解决了传统QEM算法简化模型造成特征丢失、网格过于均匀的缺点。通过实验结果可知，改进算法时间开销较其他2种算法有所增加但差别较小，在可接受的范围内。在模型简化率较高时，模型简化平均误差稳定在0.069 mm内，并且能够生成质量较高简化模型，有效防止模型特征部位退化，对于提高虚拟战场仿真场景模型加载速度以及人机交互流畅性具有重要作用和积极意义。下一步工作需要设计并行计算程序，采用GPU提高算法效率，同时在TCPGF算法的基础上考虑纹理、光照等多维因素的影响，实现对带有纹理模型的简化。