基于初高中衔接研发课例,促进学生深度思考
冒昌梅

摘 要:初、高中衔接课程不能只是在知识点上进行补充或拓展,还需要在解题策略、数学思想方法上进行拓展与训练.以“直线和抛物线相交问题”为例,可以体现初、高中衔接教学中的解题策略训练与思想方法的渗透,同时也能有效促进学生学会“深度思考”.
关键词:初高中衔接;微专题教学;直线和抛物线相交;深度思考
为帮助部分优秀学生参加热点高中自主招生考试的复习备考,学校数学组积极策划,利用集体备课进行专题课程的研发打磨,笔者承担了其中一个课时的主备任务,主题是关注“直线和抛物线相交问题”.本文整理该课的教学设计,并给出教学立意的阐释,提供研讨.
1 中考“抛物线”微专题拓展课教学设计
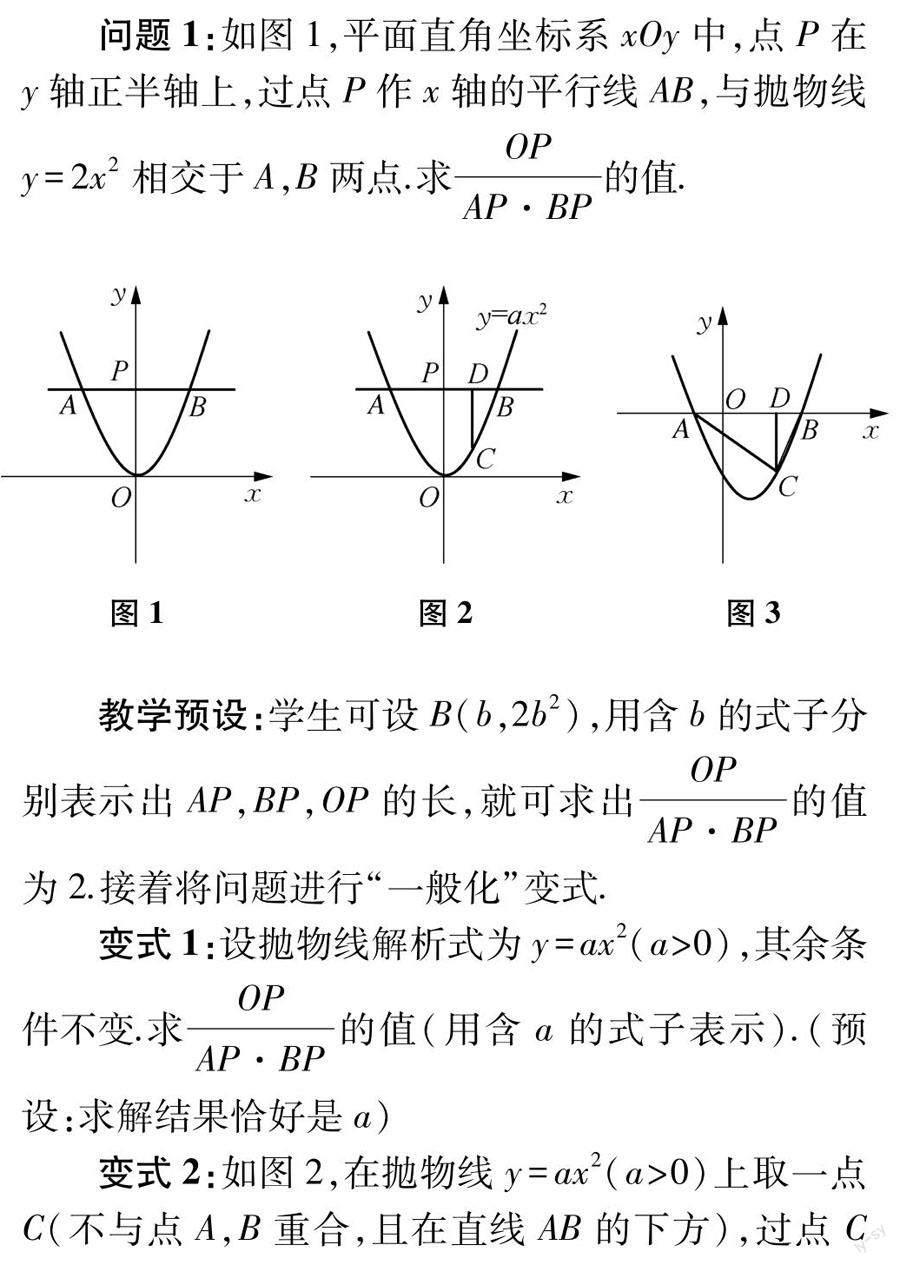
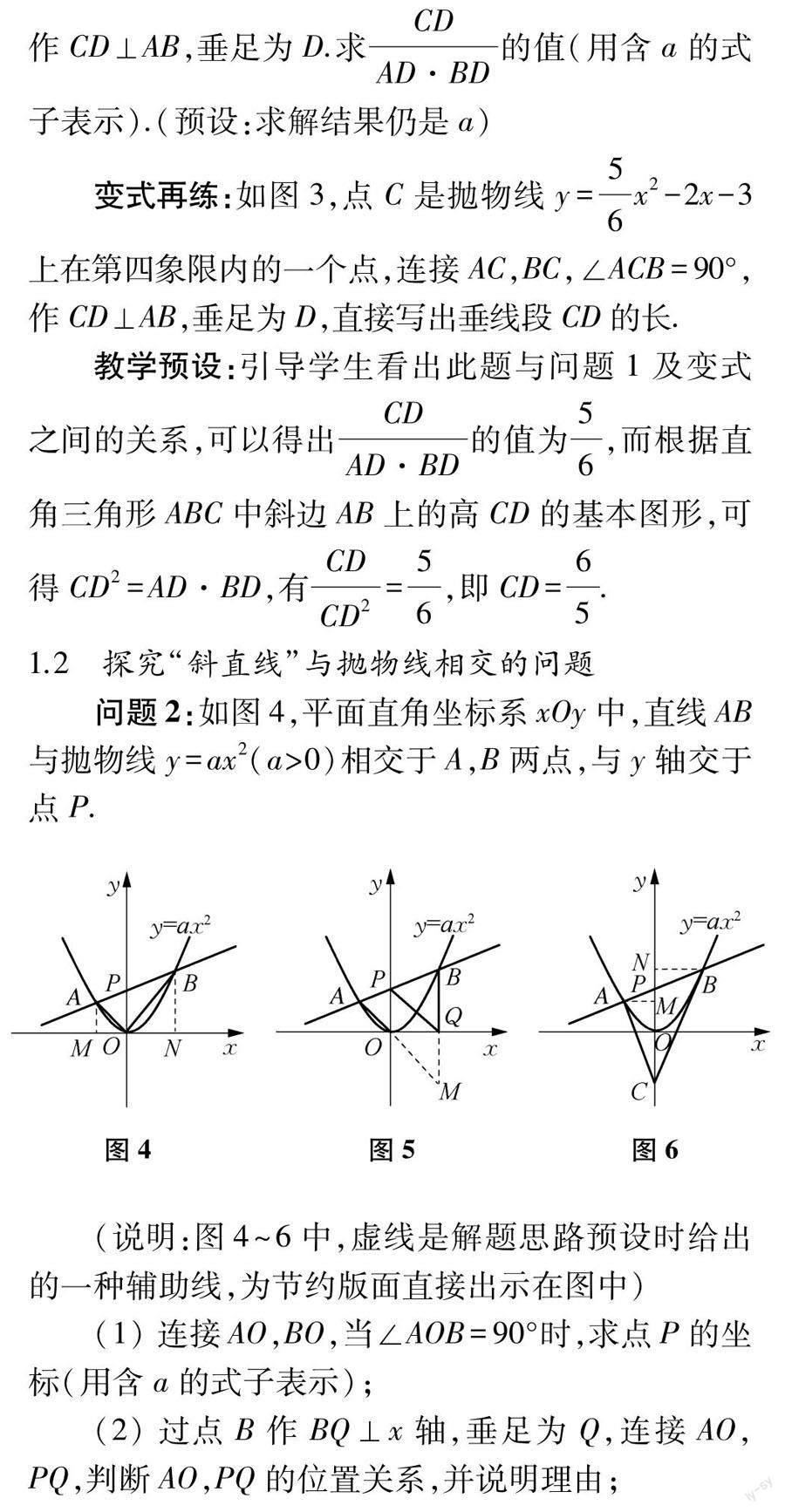
1.1 探究“水平”直线与抛物线相交的问题
1.4 课堂小结,布置作业
小结问题1:本课主要研究了直线和抛物线相交的系列問题,你对哪类问题印象深刻?结合例题说说你的理解.
小结问题2:本课学习过程中需要较强的“含参”运算能力,你积累了哪些运算或变形的经验?可结合具体的例子分享你的经验.
布置作业:
1. 整理本课研究的一些问题的解题过程.
2. 问题2、问题3中抛物线的顶点都在原点上,如果将抛物线进行适当平移,有些性质是否还成立?课后继续“一般化”地深入思考,可将其整理成数学小论文提交.
2 关于中考微专题拓展教学的进一步思考
2.1 精心选编初高中衔接内容,研发微专题拓展课
初高中衔接教学是一个值得深入研究的课题,目前不少这方面的教辅资料或课程资源主要集中在对一些知识点的补充上(比如补充因式分解的十字相乘法、二次根式分母有理化等),然而具体到初高中的数学思想方法上的衔接教学研究还不太多见.上文课例中,我们围绕直线与抛物线相交的系列问题,训练学生“含参”运算、代数推理等能力,在一定意义上也是在积极开展初高中衔接教学研究.顺便提及,当前很多地区的热点高中的自主招生考试中,也会出现本文所关注的直线与抛物线相交的变式问题或等价问题,从提优训练或复习备考的角度来看,也是值得积极实践的.
2.2 预设变式问题串留白呈现,引导学生深度思考
文[1]中指出“教师在备课时应根据课型、教学内容、学生情况等因素对课堂留白进行预设.”在上文课例中,我们选编三个“主问题”,并在每个“主问题”下预设了变式问题串,这样做可以促进学生围绕一个主问题进行深度思考.教学时,教师可“留白式呈现”每个主问题的系列变式或拓展问题.具体来说,课前不必将本课待讲评的主问题及系列变式全部印发在学案上提前发给学生,为了节约学生课堂上反复画坐标系及抛物线y=ax2(a>0)的时间,可以提供一些备用图印发给学生,其余的问题都在教师的课件中渐次呈现、留白式呈现.让专题课也能上出探索未知领域的味道.
2.3 通过课堂小结回顾与反思,继续探究“成果扩大”
涂荣豹教授在文[2]中认为:“解题学习中某些解题策略可以通过经验式概括而获得,共同特征是解决这类问题的具有一般意义的规律.”在上文课例中笔者带领学生探究直线和抛物线相交的系列问题,由于课堂教学时间有限,要取得较好的学习效果,还需要学生课后继续回顾、梳理,这也是学生将解题策略进行概括的时间保证.此外,在作业布置中还要求有能力的学生以“数学小论文”的方式整理“直线和抛物线相交问题”,这也是在积极实践宁连华教授所提出的数学教学要重视“教深度思考,教合理变换,教运算思维,教精准表达”[3].
参考文献:
[1] 蔡甜甜,刘国祥,宁连华.数学课堂留白艺术的理论探析与实践反思[J].数学教育学报,2018,27(6):29-32.
[2] 涂荣豹,陈嫣.数学学习中的概括[J].数学教育学报,2004(1):17-22.
[3] 宁连华.指向核心素养的数学高考评价及教学转向审思[J].中学数学月刊,2022(11):1-4.

