BOPPPS模式在高中数学课堂教学中的应用

陈神玉 罗亮 杨月贵 王康飞 彭焕光

摘 要：新形势下教育改革对课堂教学提出了新的要求，课堂教学要考虑学生的全面发展，展现学生的主体性.BOPPPS教学模式强调学生参与学习，并在教学过程中根据学生的反馈信息及时调整后续教学内容.本文以函数的单调性为例，构建基于BOPPPS模式下的教学设计，分析在课堂上培养学生数学学科核心素养、提升综合素质具有的应用价值.

关键词：BOPPPS模式；高中数学；课堂教学；函数单调性

高中阶段是学生成长的关键期，在学习上表现出强烈的选择性，个人兴趣与情绪往往对其学习造成很大的干扰.同时高中阶段课程多、难度大，在当下高考选拔人才的教育背景下，学生学习压力倍增，成绩分化现象尤为严重.这就要求在教学活动中，教师采用合适的教学方法和手段传授知识，同时促进学生能力的提升，思维状态的发展，使教师教有所得，学生学有所获.

针对高中数学课堂教学改革，本文以《函数的单调性》为例，设计基于BOPPPS模式的教案，通过教学评价表说明其有效性.

1 BOPPPS教学模式简介

BOPPPS模型的核心有两点，一是强调学生参与式学习；二是在此过程中可以及时获得学生反馈的信息，并以此为依据来继续调整后续的教学活动.

BOPPPS模式分为六个环节：bridgein（导入）、objective（學习目标）、preassessment（前测）、participatory learning（参与式学习）、postassessment（后测）、和summary（总结）.以上六个基本要素根据课程需要改变顺序，彼此串连起来形成了一个完整的、有效的、高效的课堂.可以说BOPPPS是一个“有效果”、“有效率”、“有效益”的“三有”教学模式.

2 基于BOPPPS模式的教学设计-以函数的单调性为例

“函数的单调性”是人教版高中数学必修第一册第三章第二节《函数的基本性质》第一课时的内容.函数的单调性是函数的重要性质之一，它刻画了函数的增减变化规律，函数单调性的知识是今后研究具体函数的单调性理论基础；研究函数性质的数形结合思想将贯穿于整个高中数学学习.本节内容十分有代表性，在解决函数值域、定义域、不等式、比较两数大小等具体问题中均有着广泛的应用；在历年的高考中对函数单调性的考查都有涉及.

针对BOPPPS模型融入高中数学的课堂教学设计：

（1） 导入环节能够使学生将新、旧知识相联系，将之前所学的相关数学知识迁移到现在的学习中.

本节内容在导入环节设定以下问题：

在第23届奥运会上新中国首次参加就获得15枚金牌，随后第24届-29届奥运会中国分别获得5枚、16枚、16枚、28枚、32枚和51枚金牌的好成绩，请画出散点图.

通过学生亲自绘制图象，清晰看到从1996年第26届奥运会开始，中国所获得的金牌数不断增加，这充分说明了我们祖国的繁荣富强和体育事业的飞速发展，增强民族自信.

（2） 学习目标可从知识目标、能力目标、德育目标进行设计.这种可观察、可衡量的学习目标组织形式培养和激发学生的学习兴趣，同时它既指引教师授课，也能让学生明确学习的方向.

1） 知识目标

① 了解单调函数、单调区间的概念，能说出单调函数、单调区间这两个概念的大致意思，并能根据函数的图象指出单调性、写出单调区间.

② 通过对金牌数变化图进行观察——猜想——推理——证明，进一步熟悉函数单调性.

2） 能力目标

① 引导学生通过观察、归纳、抽象、概括，培养自主建构单调增函数、单调减函数的概念的能力；

② 培养运用函数单调性概念解决简单的问题的能力；使学生体会特殊到一般，简单到复杂，具体到抽象的研究方法；

③ 渗透数形结合的数学思想，培养学生发现问题、分析问题、解决问题的能力.

3） 情感和育人目标

① 在函数单调性的学习过程中，使学生体验数学的科学价值和应用价值，培养学生善于观察、勇于探索的良好习惯和严谨的科学态度.

② 通过数据的变化，深刻认识到我们祖国的繁荣富强和体育事业的飞速发展，增强民族自信.

（3） 课堂中前测能够让教师摸清学生的情况，也能为后续的课堂讨论定下基调，充分体现因材施教理念.

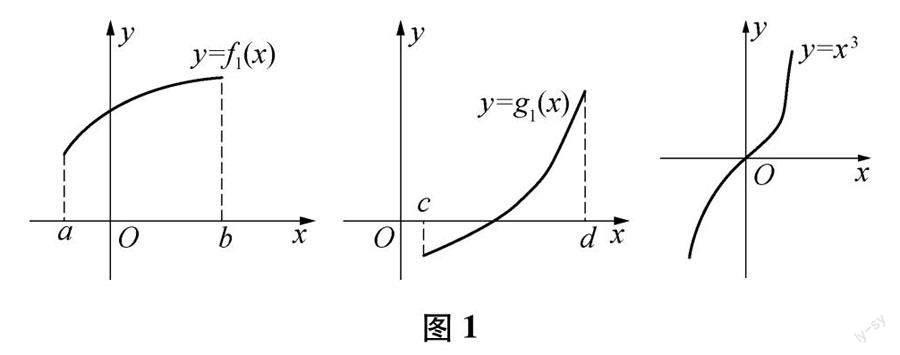
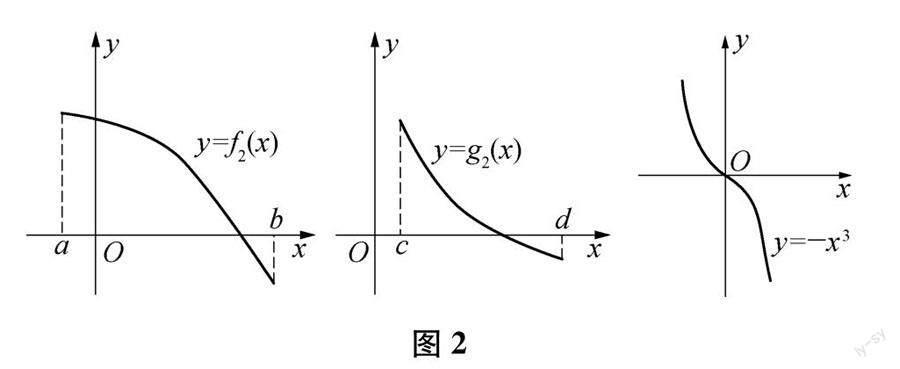
请同学们观察下面两组在相应区间上的函数，然后指出这两组函数图象的主要区别是什么？

第一组：

第二组：

让学生观察不同的函数及其图象的变化趋势，引出函数的一个重要性质——函数的单调性.

（4） 学生参与以学生为中心的课堂的交流学习实践，此教学模式体现了师生互动、生生互动；学生通过小题的小测试、小检验等方式将学习聚焦在目标上，高效地对知识进行深入地学习.同时，教师要注意加强师生互动，了解学生在目前学习阶段的学习成效.

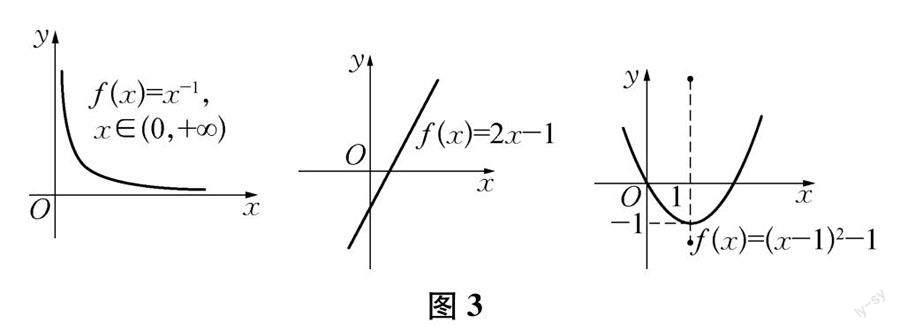
问题1：说一说图3所画函数的图象的变化趋势.（下面打出部分函数的图象）

问题2：你能明确地说出“图象呈逐渐上升趋势”的意思吗？此时X与函数值Y如何相互影响的？

问题3：我们刚才已经对函数的单调性，做了定性的分析，我们如何从量的角度来刻画这种性质.你能给出一个确切的定义来吗？请用你自己的话表达出来，并说给你的小组成员听，与他交流后，形成集体意见，再展示给大家.

这部分内容采用的授课方式：对每一个问题，小组成员先独立做，再分别说出自己的想法，然后讨论，形成集体的意见.

小组内成员合作，组间成员的竞争讨论是一种有效的教学策略，使得整个评价的重心由个人之间竞争转为团体合作达标，并能使教师与学生、学生与学生之间有更多的交往、互动的机会.它也是引导学生积极参与教学过程的重要措施，是培养学生合作精神和激发学生创新意识的重要手段，也是促使每个学生得到充分发展的有效途径.

本题难度较大，学生难以从中归纳出证明方法及步骤，因而有必要先详细讲解，通过分析、引导学生抽象、概括出方法及步骤，提示学生注意证明过程的规范性及严谨性.其次归纳证明方法并加以比较说明，使学生突破本节的难点，掌握重点内容.

通过一系列的问题，引发对概念的全面思考.从具体到抽象，再从抽象到具体，通过合作交流，增强学生对概念的理解，不断地修正、完善结论，达到建构数学的目的.

（5） 后测部分教师可以通过类型丰富的选择题、判断题、问答题、开放性问题对课堂的教学成果进行系统性检测，学生可以灵活地应用这种自检互检的方式了解自己在整堂课上的学习成果，并且对自己目前的学习水平有一个整体的认知，从而将课堂内容应用于实践，解决了学生反映数学课程“学而无用”的情况.

根据函数图象说明函数的单调性：

本次教学设计在54人的班级中进行教学，上课过程动静结合，学生思维活跃，讨论过程积极主动，对函数单调性有较深的理解，对本节课的知识掌握牢固，并能够形成知识体系框架.

3 结束语

本文给出了《函数的单调性》课程中应用BOPPPS教学模式的一个课程设计内容，为高中数学的教学模式提供参考.模式架构应用可根据不同授课内容和学情分析，灵活调整六个模块的完整性，不用拘泥于模块的顺序性，做到更加契合当代中学生的心理特征、接收程度和认知规律.

BOPPPS教学模型能够在一定程度上弥补传统教学模式的不足，强调学生的主体地位、侧重教学目标清晰明确地向学生展示，注重课后反思和教学反馈，学生的创新能力和合作意识也随之潜移默化地增强了，实现高效果、高效率、高效益的有效教学.

参考文献：

［1］ 曹丹平，印兴耀.加拿大BOPPPS教学模式及其对高等教育改革的启示［J］.实验室研究与探索，2016，35（2）：196-200+249.

［2］ 唐慧羽.BOPPPS模式下高等数学微课教学设计策略的探讨——以“曲线的凹凸性”为例［J］.教育观察，2019，8（20）：55-57.

［3］ 王萌，朱玉清.基于BOPPPS模型的高等数学课堂教学设计——以“定积分概念”为例［J］.知识文库，2019（17）：59-60.

［4］ 杨超，韩振来，孙书荣.BOPPPS教学模式在高中数学教学的应用——以“瞬时速度与导数”为例［J］.Proceedings of 2018 3rd International Conference on Education Research and Reform （ERR 2018）（Advances in Social and Behavioral Sciences，VOL.24）.

［5］ 閻岩.BOPPPS教学模式下高中生数学态度的研究——以济南市S中学为例［D］.济南大学，2020.

［6］ 樊欣，马小琼，韦华益，唐剑岚.动感技术的融合提质增效数学教学——以“反比例函数图象与性质”教学片段为例［J］.数学之友，2022，36（2）：88-89.

［7］ 马洪超.打造“极简理念”下的生态数学课堂——以《函数与方程》一课为例［J］.数学之友，2022，36（3）：32-33.

［8］ 陈万寿.从三个事件互相独立的条件谈起［J］.数学之友，2022，36（3）：55-56.

［9］ 罗理想.高考数学解析几何考查状况分析——以2021年高考数学全国二卷为例［J］.数学之友，2022，36（3）：81-82.

［10］ 张娟.简洁中的深刻，朴实后的精彩——构建指向深度学习的有效课堂［J］.数学之友，2022，36（4）：21-22.

［11］ 吕亚琼.捕捉瞬间，“问”出精彩——浅谈初中数学课堂的有效提问策略［J］.数学之友，2022，36（4）：49-51.

［12］ 吴紫娟.平板电脑在函数教学中应用的课例与反思［J］.数学之友，2022，36（4）：81-83.

［13］ 张倩，沈威.一道中考销售类试题蕴含模型思想的探究［J］.数学之友，2022，36（5）：5-7.

［14］ 兰育哲.回顾促思 层层推进——“长方体和正方体”单元复习的思考［J］.数学之友，2022，36（5）：52-53.

基金项目：2018年度广东省高等教育教学改革项目“面向新工科《数学分析》课程之‘对分课堂教学改革研究与实践”（编号：531）.