高中数学运算素养的学习进阶研究
沈敏忠


摘 要:基于学习进阶理论在学科教学中的逐渐渗透使用,以及新课标提出的数学课堂教学要关注数学核心素养的形成和发展两大背景,本文尝试在学习进阶理论的指导下,以平面向量數量积运算作为教学研究对象,实践探索在课堂教学中,如何结合学生的认知基础和认知发展规律,为学生合理的搭建适宜学习的进阶点,使高中学生在数学课堂中能更好地提高数学运算核心素养.
关键词:学习进阶理论;数学运算核心素养;平面向量
1 研究背景
1.1 学习进阶理论
学习进阶理论起源于美国科学教育领域,美国国家研究理事会(简称NRC)对学习进阶的概念界定为:“学习进阶是学生连贯且逐渐深入的思维方式的假定描述,在一个适当的时间跨度下,学生学习和探究某一重要的知识或者实践领域时,其思维方式逐渐进阶.”
学习进阶理论常描述学习者在学习某一模块内容时,需要分阶段学习这一内容,通过不断深化前一阶段内容的认知结构,促进对核心概念的理解,后一阶段对该概念的学习都是以拓展前一阶段的内容为线索,最终目的是促进学生学科素养的发展.
近年来,学习进阶理论逐步进入数学等学科教学领域.
1.2 数学教学要关注学生数学核心素养的形成和发展
《普通高中数学课程标准(2017年版)》指出:高中数学课程要面向全体学生,更多关注数学学科核心素养的形成和发展,促进学生在不同学习阶段数学核心素养水平的达成.数学运算是数学学科的六大核心素养之一,是解决数学问题的基本手段,几何与代数是高中数学课程的主线之一,而向量是沟通几何和代数的桥梁,运算是向量的灵魂,所以借助构建向量运算的学习进阶,是提升学生数学运算素养的一种良策.
基于上述研究背景,本文拟以“平面向量的数量积运算”作为研究对象,遵循数学概念建立的逻辑性和层次性,对研究对象分别进行静态、动态的分阶划分,积极思考如何科学设置学习的进阶点,引导学生有序建构,期望最终能实现学生数学运算素养的有层次生成.
2 基于学习进阶理论的研究对象和学情分析
2.1 研究对象分析
教材选用人教A版(2019版)必修第二册6.2.4章节内容,教材分为2个课时,第一课时介绍数量积的概念,第二课时介绍数量积的运算律.《标准(2017年版)》指出,在必修课程与选择性必修课程中,突出几何直观与代数运算之间的融合,即通过数与形的结合,感悟数学知识间的关联,加强对数学整体性的理解.向量的数量积是向量运算中的一个重要部分,在学习了平面向量的基本概念、平面向量的加法、减法、数乘这些线性运算后,再继续学习平面向量的数量积运算,深化向量运算,让学生完善平面向量的运算体系,感受平面向量的运算魅力.受教学课时影响,本次实践教学以《平面向量数量积运算》第一课时作为研究对象,主要介绍平面向量数量积的概念以及简单计算,对概念本身的处理.为了能更好地承接前面所学的向量的线性运算,课堂教学时没有先从物理做功的角度引入数量积,而是从代数运算角度入手,通过对运算结果的合理分析来引出平面向量数量积的概念,并进一步从几何直观、物理融合等多角度对数量积概念加以深化理解.
2.2 学情分析
该段学习内容的学习对象为高一年级学生,学生在物理知识方面已经学习了“力”“功”等相关内容,经过向量前段时间的学习,对平面向量的概念,向量的加法、减法、数乘这些线性运算及其相应的运算律有了一定的认识.
3 研究对象的学习进阶划分
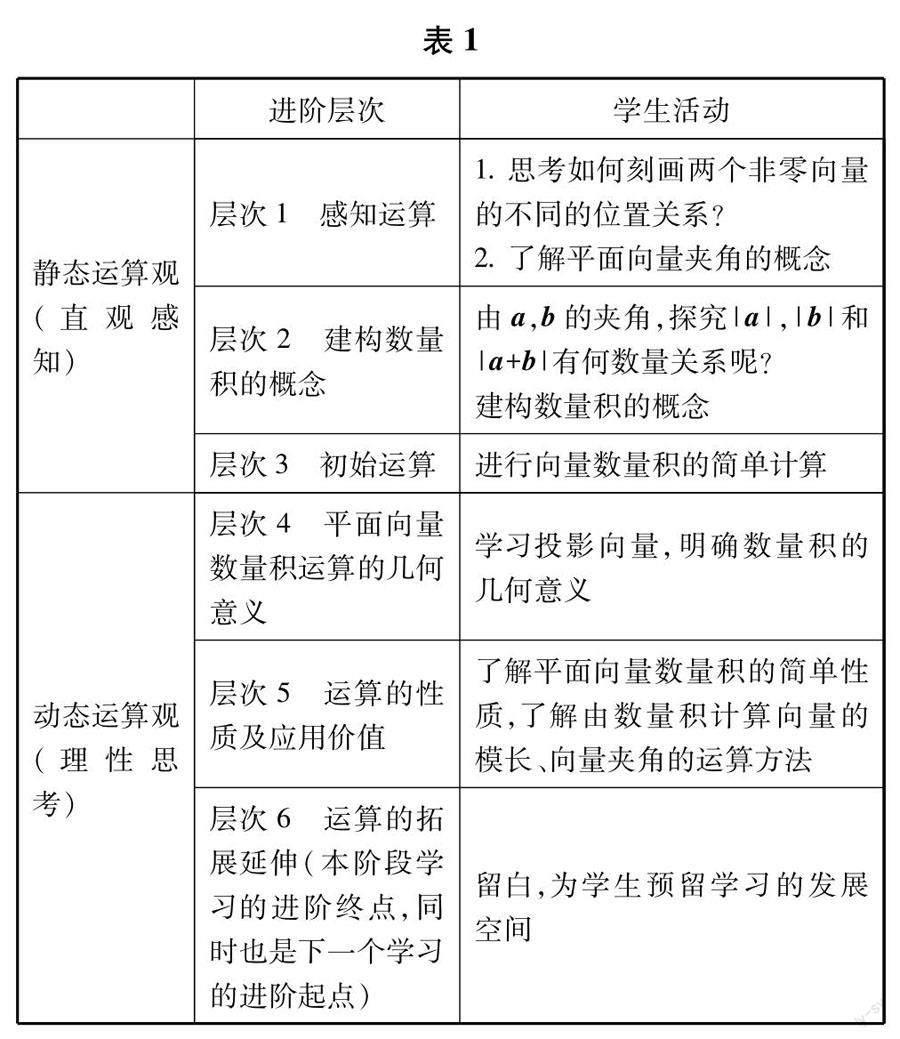
基于学习进阶理论的过程设计,笔者认为应该首先确定学习进阶的起点和终点,高度重视由进阶起点到进阶终点的进阶序列的搭建,恰当划分进阶的层级.为了促进高中数学运算素养的提升,首先需要明确具体的数学运算是什么,可以以此作为学习进阶的起点,围绕是什么(概念),怎么算(运算律),与其它运算的横纵联系(内涵外延),以及运算可以干什么用(运算实际应用)等系列问题,提高学生对数学运算的多维度感知,从而积极提高学生的数学运算核心素养,达到学习进阶的终点.为此,将平面向量的数量积教学第一课时进行了如下层级的学习进阶划分(如表1).
4 具体的学习进阶实践
对照表1的学习进阶划分,本节课笔者将向量数量积的运算教学按照确定学习进阶起点→生成概念→简单计算→探寻运算的几何意义→学科跨界融合→性质探究→课堂小结的进阶线路展开,具体实施如下:
4.1 明确学习进阶的起点
前面我们已经学习了向量的加法、减法运算,类比实数的运算,向量能否相乘?如果能,那向量的乘法该怎样定义?
设计意图:在课堂引入环节,从类比实数运算的角度来激发学生的学习兴趣,引导学生对未知领域积极探索.
我们知道平面向量有大小、方向两个要素,我们用模表示向量大小,用带箭头的有向线段表示方向,对单个向量的方向认知,经历了从起点到终点的直观感知,到借助坐标表示向量的精准定位的过程.对两个非零向量,我们还可以从考查它们的位置关系入手进一步理解向量两个要素的内涵.我们可以如何刻画两个非零向量的不同的位置关系?
设计意图:让学生直观感知可以用向量夹角来刻画两非零向量的不同位置关系,介绍平面向量夹角概念.
将最基本的向量加法运算作为学习的进阶起点,开展对若干向量模长关系的定量计算研究,有利于向量运算由加法到乘法的前后承接,探究活动中关注对运算过程进行由特殊到一般的思维训练、运算结果进行理性定量思考,这些思维活动有助于培养学生的逻辑推理、数学运算等核心素养.
向量有着丰富的物理背景,在物理中,如果物体在与运动方向成角度θ的力的作用下,产生位移s,那么如何计算力对物体做功的大小?功的计算公式与向量的数量积有什么联系?
从数学角度来看,力和位移都是向量,做功大小的计算过程从运算角度理解,可以抽象为两个向量的运算问题,如何看待向量与向量的这种乘法运算?该运算与以往学过的向量加法、减法、数乘运算在运算结果上有什么差异?
设计意图:给出向量数量积的定义后,再联想物理中功的计算,可以增强学科间的融合,增加对数量积概念的理解,同时也能很好地发展学生的数学抽象能力.通过与以往的向量线性运算的结果进行比较,感受差异,让学生明确向量数量积的运算结果是数量,而非向量.
4.3 数量积的初步简单计算
4.6 课堂小结,留置探究空间
每一种运算都有相应的运算法则,类比实数的乘法运算律,思考数量积有类似的运算律吗?
5 基于学习进阶理论的教学反思
本节课在教学设计时运用了学习进阶理论,考虑到向量本身兼具数形两方面的属性特征,逐层引导学生熟练掌握理解公式,从教学进阶起点的设置到数量积的概念引入,探寻数量积的几何意义,再到思考数量积的简单性质,层层递进,多角度帮助学生构建并加深对向量数量积运算的再認识.具体流程如下:
学习过程中,针对平面向量数量积概念的生成,设置不同的学习进阶点,引导学生从具体到抽象,帮助学生逐级构建并加深对平面向量数量积概念的再认识,学生的主体地位得到了充分的彰显,教师的主导作用得到了有效体现,学生探究问题的能力、数学运算以及对运算结果的处理分析能力得到了有效锻炼,在探究环节中还渗透了由特殊到一般的数学思想,课堂教学实现了从简单学习知识到培养数学思维、提升数学核心素养的全面进阶,基于学习进阶理论的教学尝试有利于促进数学学科核心素养的落地生根.
参考文献:
[1] 刘晟,刘恩山.学习进阶:关注学生认知发展和生活经验[J].教育学报,2012,8(2):81-87.
[2] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
[3] 教育部课程教材专家工作委员会.《普通高中数学课程标准(2017年版)》解读[M].北京:高等教育出版社,2018.
[4] 周军.学习进阶视域下的数学大概念深度学习实践[J].中学数学(高中),2020(19):92-94+97.
[5] 章建跃.核心素养立意的高中数学课程教材教法研究[M].上海:华东师范大学出版社,2021.
[6] 张玉峰.基于学习进阶的科学概念教学内容整合[J].课程·教材·教法,2019,39(1):99-105.
基金项目:江苏省教育科学“十三·五”规划课题“学习进阶理论下数学核心素养培养的实践研究”(课题编号:B-b/2020/02/156);江苏省“十三·五”规划课题“数学核心素养导向下学习文化建设研究”(课题编号:C-c/2018/02/78).

