增强问题意识 提升核心素养
王彪

[摘 要] 问题意识是指思维的问题性心理,人在认知过程中经常会遇到一些不明白的问题或现象,由此产生一探究竟的心理。数学教学应着重培养学生的数学核心素养,让学生会用数学的眼光发现并提出问题。在课堂教学中,教师对于学生问题意识的培养还存在不足,文章以“3的倍数特征”一课为例,通过分析这些不足,提出增强学生问题意识、提升学生核心素养的策略。
[关键词] 问题意识;核心素养;3的倍数
课堂教学中有这样一种现象:老师会经常性地鼓励学生要不懂就问,遇到问题要多问几个为什么。然而学生这边却是一头雾水,不知道问什么,不清楚怎么问。这不得不引发我们的思考,是不是作为执教者的我们在培养学生的问题意识上出现了问题呢?
问题意识是指思维的问题性心理,人在认知的过程中经常会遇到一些不明白的问题或现象,并且通常会产生一探究竟的心理。伟大的教育家陶行知先生说:创造始于问题,有了问题,才会思考,有了思考,才有解决问题的方法,才能产生独立思考的可能。好的问题不仅可以激发学生学习的欲望,还有助于学生加深对知识和方法的理解、探究学习的本质,引发学生高质量的思维活动。《义务教育数学课程标准(2022年版)》也指出,要能够在实际情境中发现和提出有意义的数学问题,进行数学探究;形成对数学的好奇心与想象力,主动参与数学探究活动,发展创新意识。当下“满堂灌”教学得到较大改观,但教师对于问题意识的培养仍存在一些问题,下面以“3的倍数特征”的教学为例,谈谈问题意识的问题及解决对策。
一、问题意识的课堂现象与分析
现象一:问题偏多,学生缺少了思维的时间。如一位教师在教学中,与学生进行了如下的对话。
师:2、5的倍数有什么特征?
生(齐):2的倍数,个位上是2、4、6、8、0。
5的倍数,个位上是0、5。
师:3的倍数可能会有什么特征?
生1:个位上是3。
生2:个位上是3、6、9。
师:果真如此吗?让我们验证一下吧。
学生举例。
师追问:这些数的个位上是不是都为3、6、9呢?
生(齐):不是。
师:那个位上是哪些数呢?
生(齐):0、1、2、3、4、5、6、7、8、9都有可能。
……
在这个过程中,教师将一个核心问题“3的倍数是不是也像2、5的倍数一样只看个位就可以了”,生生地分解成了接连不断的若干个问题,看似有序,實质上却剥夺了学生独立思考的机会。接连不断的提问,会让学生无暇去思考,这样就变成了教师与学生之间的“一问一答”式的对话,激发不了学生的思维活动,而问题的设计目的应该是为了激发学生的思维,引起学生的深度思考。
现象二:问题偏易,学生缺少了思维的空间。比如在学生发现个位上是3、6、9的数不一定是3的倍数时,教师又进行了这样的提问:“刚刚发现个位上是3、6、9的数不一定是3的倍数,那十位上是3、6、9的数行不行呢?”学生答:“不行。”“那百位呢?”学生又答:“也不行。”“那其他数位呢?”学生齐答:“都不行。”像这样逐个提问个位、十位、百位等等数位行不行的问题,对学生而言毫无难度,不需要思考便可回答,也引发不了什么数学思考。
现象三:问题带有指向性,限制学生的思维发展,失去问题的价值。再如还是在发现3的倍数不能靠个位来判断时,有教师又这样提问。
师:请同学们斜着看一下3的倍数,观察这些数各个数位上的数字的和,你有什么发现?
生1:1+2=3,2+1=3。
生2:1+5=6,2+4=6,3+3=6,4+2=6,5+1=6。
生(齐):每一斜行的和都一样,都是3的倍数。
……
教师机械地让学生观察斜行中“3的倍数特征”,学生在教师的指引下只需要进行计算,稍微动点脑子便可轻松发现规律。其实,这是用教师的思维代替了学生的思维,学生按照教师铺好的路子走下去就一定不会出错,也就不会再有“问题”,但这样的做法却限制了学生的思维发展。
二、问题意识的课堂梳理及实施
1. 在问题情境中,提出“真”问题
《义务教育数学课程标准(2022年版)》指出,教学应为学生提供丰富的问题情境、充分的思考空间,让学生经历观察、实验、猜测、推理、交流、反思等数学活动过程,帮助学生感悟基本思想,积累基本活动经验。基于此,要求教师在组织教学活动时,要能够激发学生学习的欲望,引发认知冲突,提出“真”问题,为深度思考搭建平台。
复习:前面我们研究过2和5 的倍数,那它们各有什么特征呢?我们是怎么研究的?板书:找数、观察、猜想、验证、归纳。今天,我们来研究“3的倍数特征”。
出示“百数表”。
师:你能从表中找出3的倍数吗?找出来后说一说,这些数有什么特征?
学生以组为单位探究、交流、汇报。
生1:个位上1、2、3、4、5、6、7、8、9、0的数都是3的倍数。
生2:不对!这些数有的是3的倍数,有的不是3的倍数。
生3:个位上是3、6、9的数都是3的倍数。
生4:也不对。像13、26、29都不是3的倍数。
生5:这说明不能以个位上的数来判断一个数是不是3的倍数。
师:那怎么办呢?还能再观察出一点别的规律吗?
生6:我发现横着的数每隔两个数就是3的倍数。
生7:竖着的数也是每隔两个数就是3的倍数。
生8:我发现,斜着看,第一斜行的数的各个数位上的数字加起来是一样的,都是3;第二斜行的数的各个数位上的数字加起来是一样的,都是6;第三斜行的数的各个数位上的数字加起来是一样的,都是9。
……
在这个教学过程中,教师把问题抛给学生,学生先是利用2、5倍数特征的经验去探寻“3的倍数特征”,发现从个位上来判断3的倍数是行不通的,引发新的问题冲突。学生转变思考路径,先横着看再竖着看,从数的组成上去尝试能不能找到答案,经历了先发现规律,再否定规律,接着继续寻找规律的过程。这个过程,教师围绕“3的倍数特征”这个核心问题,利用“真”问引发“真”思考。也许学生发现的规律不一定正确,对于研究也不一定有帮助,但这些都促使了他们去发现问题、分析问题,只有这样才能为深度思考搭建平台。
2. 在问题驱动下,经历“真”探究
人类认识的过程总是从实践、探索开始的,是一个从无到有、从低到高、从慢到快的过程。研究“3的倍数特征”的难度大于研究“2、5的倍数特征”的难度。知识与学生之间存在巨大的鸿沟,教师既不能把研究的规律灌输给学生,又不能手牵手地带领学生去重走一遍特征发现之路,而需要让学生重新认识知识产生、发展的关键环节,让学生在实践探究中发现知识、建构知识,促使学生经历面对表面现象去深度探究的过程。
在上述引发冲突之后,教师组织如下探究活动。
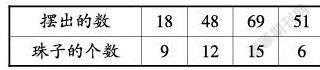
师:只看个位、十位都不行,那就要十位、个位一起看。为了方便观察,我们在计数器上拨一些数。比如15,一共用了几个珠子?
生1:6个。
让学生再拨24、42、51、60。
师:你有什么发现或想法呢?
生2:都用了6个珠子。
生3:这些都是3的倍数,拨出的珠子的个数也都是3的倍数。
生4:珠子的个数和3的倍数有没有关系呢?
出示活动单,学生在百数表上找出3的倍数,在计数器上拨一拨。
出示部分数据,引导观察。
生(齐):拨这些数用的珠子的个数是3、6、9、12、15、18,它们都是3的倍数。
……
在上述教学过程中,教师并没有让学生直接计算个位、十位上的数的和,发现这个“和”与3的倍数的关系,而是引导学生带着问题、带着冲突,回归数的组成,经历拨珠、算珠个数、猜测、推理、实验等活动,在拨珠的过程中直观地发现拨出的珠子的个数是3的倍数。因为从学生的思维角度出发,他们很难想到个位、十位上的数的和与3的关系,但有了拨珠的经历,学生就更容易想到珠子的个数与3的倍数的关系。在這一活动中,学生不是被动地去接受外在知识,也不是从实践开始盲目实验,而是通过主动的有目的的活动,去自主发现“3的倍数特征”。有了学生的全身心投入,深度思考才能悄然发生。
3. 在问题验证中,实现研究转向
爱因斯坦说,学习知识要善于思考、思考、再思考。是的,学习知识不能一蹴而就,不是一次思考就可以完成的,而是要反复思考,正反向同时论证。先思考得出猜想,再思考验证猜想,接着思考生成新的问题,最后完善结论,就是在这样一个循环往复的思考中学生的思维不断发展。
在学生获得发现、提出猜想后,教师扩大举例范围。
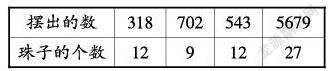
师:刚刚我们研究的百数表,发现拨这些数用的珠子的个数都是3的倍数。现在可以下结论了吗?
生1:不可以。还要研究更大的数。
师:怎么找到更大的3的倍数。
生2:用3乘更大的自然数。
学生活动,教师指导。学生填表,展示交流。
师:通过研究更大的数,你有什么发现?
生3:拨是3的倍数的数,所用的珠子的个数也都是3的倍数。
师:那如果不是3的倍数,珠子的个数还会是3的倍数吗?
学生继续操作实验,得出:拨不是3的倍数的数,所用的珠子个数也不是3的倍数。
反向研究。
师:那反过来,组成一个数的珠子的个数是3的倍数,那这个数就一定是3的倍数吗?
学生继续拨珠实验。
在上述教学过程中,随着研究的对象从百数表到更大的数,研究的范围不断扩大,产生新的问题:对于更大的数,发现的规律是不是也成立呢?如果不是3的倍数,珠子的个数还会是3的倍数吗?这样让研究问题从片面走向全面。接着,从正向研究转向反向研究:如果珠子的个数和是3的倍数,那么这个数是不是也一定是3的倍数?这样的问题研究由片面到全面,由正向到反向。在这一过程中,学生的思考也由浅入深、由表及里,走得更深、更广。
4. 在问题反思中,发现数学理性
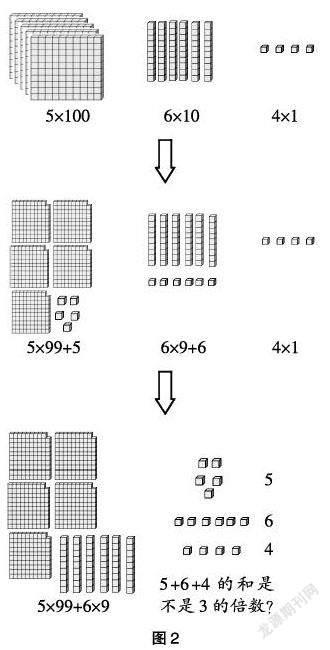
数学是讲“理”的学科,对于一个规律的形成,如果让学生仅仅经历探究、发现、总结规律的过程,而不让学生明白其中的道理,那只能是知其然,学生也就无法领悟数学学习的意义与价值。探究了“3的倍数特征”之后,学生心中一定会有这样的想法:2和5的倍数可以从数的个位来判断,为什么3的倍数要从各个数位的和来判断呢?带着这样的问题,在总结“3的倍数特征”时,教师又借助直观对规律进行了解释。举例564、288、672等数,通过多媒体直观演示,配合数的组成进行推理。如564=(5×100)+(6×10)+4=(5×99+5)+(6×9+6)+4,判断564是不是3的倍数只要看5+6+4的和是不是3的倍数就可以了,如图2。经历了这一教学过程,从现象到道理,进而发展学生的推理能力与理性精神。
问题是数学的心脏,实践证明,教师通过问题引领能有效诱发学生的深度思考。学生经历观察现象、提出问题、分析问题、解决问题的过程,激发了创造性思维,提高了解决现实问题的能力,发展了核心素养。

