基于真实情境的初中数学课程转化
张依淼 鲁荣章



【摘 要】情境教学法在教学设计领域具有重要影响,根据真实数学教育理念,情境问题是数学教育的“心脏”。本文依据真实情境教学的内涵,厘清真实情境的数学课程转化的逻辑理路,论证真实情境与数学课程设计的相融性及能力表征与课程转化之间的关联性。在此基础上,建构关联性转化的四个基本要素,即知识要素、情境要素、表征内涵、智能活动。本文辅以教学案例进行论证,以期为初中数学教学提供参考。
【关键词】情境教学法;真实数学教育;课程转化;关联性;相融性
一、引言
21世纪以来,教学设计从跨学科领域研究到信息技术方法的整合,从学习环境的建构到评估理念的转变都发生了翻天覆地的变化。“情境教学”是适应时代发展而产生的一种教学方法,它将认识论、学习心理学与教学设计进行整合。数学学科中强调真实情境的运用,是源于荷兰的真实数学教育思想[1]。美国威斯康星州教育研究中心研发出一套情境数学课程[2],主要为培养和塑造中小学生的数学能力而设计,其实质是延续了荷兰的真实数学教育思想。近些年来情境教学模式不断衍生、发展,如以情境为主导的生态化教学模式,以生活为导向的课堂教学模式等。
当今信息社会快速发展,真实情境学习在社会生活与科学技术中发挥着重要作用,它可以引导学生主动探索知识,培养学生解决生产生活实际问题的能力。高度信息化的知识经济时代对新一代学习者提出了更高的要求:碎片化、浅层化、非系统化的学习已经不能适应时代的要求,学习者需要在真实生动的情境中进行深度思考,深入参与教学,以激发自身主动学习的欲望。与传统“填鸭式”课堂教学相比,真实情境教学在教学中融入真实生动的情境,以培养学生信息获取与处理、反思、问题解决、迁移运用、人际交往等方面的能力。从这个意义上讲,真实情境教学作为一种现代教学方法,强调了对学生主体性和创造性的培养,体现了教学与生活的深度融合。《义务教育数学课程标准(2022年版)》在课程理念中提出要引导学生在真实情境中发现问题和提出问题,因此,基于真实情境的问题解决和关注学生的综合实践体验,对于启发学生思考和寻求问题解决方案具有积极的影响作用。
二、基于真实情境的数学课程转化的研究综述
从宏观分析,Shulman在其建立的教学知识转化理论中论证“教学推理与行动模式”,指出教師教学知识转化要经过四个环节——准备、表征、教学选择、调适。他特别强调表征阶段,是教师根据自己对课文的理解和领悟来决定向学生传达内容的教学方法(包括类推、隐喻、举例说明、证明、模仿),表征能让教学变得更具体。[3]从知识转化角度,王有远等认为课程转化存在隐性知识和隐性课程资源。[4]梅景瑶等认为知识转化意味着整合性多维度创新能力提升。[5]从跨学科角度,Niklas Gericke等认为强大的知识应与转化分析联系起来,并作为跨学科特定学科教学法的研究框架来发展和实施。[6]从教师教育角度,周彬认为教师教育的教学知识需要依托学科知识背景和教育科学知识才具有生命力,因此有必要进行课程转化。[7]从核心素养角度,李刚等围绕学科大概念的课程转化设计为落实学科核心素养提供指引线索,深入贯彻新时期我国课程改革中立德树人的根本任务。[8]从人才培养目标的角度,吕立杰等强调课程转化与人才培养目标的融合,指出在教材编写中,中介性转化、多形态转化、聚焦式转化、多层次转化等方式是实现培养目标的有效途径。[9]
从微观学科教学视角来看,数学学科具有其他学科所不具备的抽象性,根据Shulman的教学知识转化理论,需要通过表征将数学由抽象转变到具体,因此创设真实情境对于数学课程教学就显得十分必要。有研究者使用“真实情境的数学化”和“数学知识的数学化”这两个元素说明真实情境的创造性,认为数学概念的建立是基于人类的活动,是帮助学习者与周遭环境产生意义的一种工具。[10]国外学者认为真实情境设计对数学学习具有重要作用,Pauline Vos指出,基于真实情境产生的真实数学问题更能激发学生学习的积极性。[11]Lieven Verschaffel等认为情境问题与数学建模任务之间具有复杂关系,同时指出教科书、软件和教师是促进解决情境问题能力发展的三个重要因素。[12]仝玉婷等阐释美国EM教材数学情境设计具有表征具象、非识记型认知、路径多元、思维可视化等特点,对我国数学教材编写具有启示性。[13]李玲等也认为思维能力是数学核心素养之“魂”,真实情境设置能够促进学生思维可视化,从而产生深度教学。[14]
三、基于真实情境的数学课程转化的逻辑理路
将真实情境纳入数学课程设计,需要经历课程的相融和转化的过程。所谓课程相融,是指外在真实素材通过教师的改编,产生有意义的联结,然后内化于学生的认知结构。所谓课程转化,就是各层次的人对课程层次给出的内涵进行觉知、理解和解读后,依据这一层次的情境因素将课程整理为学生能够理解的样态和教学情境能够践行的样态,并确定下来。更为具体地讲,课程转化是指把抽象和宏观的课程标准转化为可供教学使用的课程要素(包括学习内容、教学活动和预期目标),然后利用数学工具表达与课程转化有关的概念。在由正式课程向运作课程转化的过程中,教师认识、诠释和转化能力指标需要教学活动设计和课堂实际操作来达成。
1.真实情境与数学课程设计的相融性
真实情境与数学课程设计的相融要求外在真实素材内化于学生的内在知识结构之中。数学学习是一个动态发展的过程,它具有开放性和创造性,数学教学也应符合这一特点。教师只有充分挖掘数学知识背后所隐藏的数学思想方法,才能真正实现有效的数学课堂。因此,真实数学教学有如下基本特征:运用脉络和模式;学生能够自主生成结论和构建知识;教学过程具有交互性;解题时能够整合交叉分支的知识。本文整合这些特征,设计真实情境与数学课程相融的图示模式(图1)。在真实情境的脉络下,课程设计要有意义地联结其他部分,并将符号、图示和模式等工具潜在地融入,以开放的形式呈现数学素材与问题内容,让学生在活动中能和其他人互动、探讨、交涉和合作,这样学生才有机会去做数学、沟通数学,并通过集体引导获得更自由、更开放的产出。
2.能力指标与课程转化之间的关联性
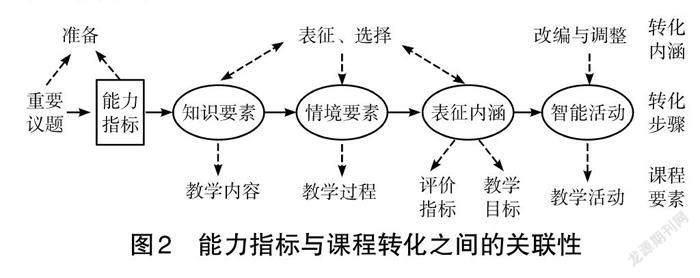
教学是推理与行动的循环,而在这个循环中,转化位于教学推理模式的中心位置,可见转化的重要性。转化的内涵包括准备、表征、选择、改编与调整等四个要素。其中,准备和表征是最基本、最重要的两个要素,它们为整个教学过程奠定基础。所谓准备,是指教学目标的厘清、概念的重组等。表征则是指运用表征,如示范、譬喻、模拟等。选择则是指教学、组织、管理等方式。改编与调整则是根据学生的特质,适时适度地调整与修正教学方式。因此,在教学之前,除了理解教学的内容知识,还应该考量学生的特质,选择适当的表征方式与教学方法,对教学内容进行适度转化,以符合优质教学所需。在本文研究中,准备是属于能力指标解读的范畴;若要进行能力指标的转化,则需要考量表征、选择这两个要素的使用与安排;而改编与调整则属于教学转化的智能。我们从能力角度进一步切入,得出结论:能力指标的课程转化培养学生正视问题,能够运用知识和有效策略来解决问题。由此可见,转化贯穿于整个教学过程,具有非常重要的作用和意义。然而,任何一个具体的教学活动都离不开一定的思维品质。所以,在能力指标课程转化过程中,需要抓住四个基本要素的内在联系,即知识要素、情境要素、表征内涵和智能活动。其中知识要素是指知识的类型与层次,可通过树状、螺旋网状等方式延伸概念;情境要素则是引导学生学习思考、问题解决或探索某项课程主题的各种挑战或问题;表征内涵是预设在教师提出问题与挑战后,学生对问题的认知与态度;智能活动是教学活动的安排。因此,教师在进行真实情境融入数学课程的设计时,要选择、改编、组织、调整、整合这些要素,才能使真实情境的融入变得更有意义。如图2所示。
四、基于真实情境的数学课程转化的教学设计——以“二元一次方程组的图像解法”为例
真实情境与数学教学内容该如何融合为一体,需要教师对数学教材进行开发利用。教学转化过程需要经历准备、表征、选择、改编与调整过程,这中间涉及学生的能力表征到课程转化。将课程内容转化为学生能力需要四个基本要素——知识要素、情境要素、表征内涵、智能活动,它们构成了由外而内的转化过程。真实情境与课程设计的相融性取决于其他外部材料与真实情境素材的相互作用过程,以及让学生建立从感性到理性的认知过程。这些转化需要教师在数学课堂中以计划、行动、观察、反省的行动研究過程不断推进。基于此,本文以初中数学中二元一次方程组的知识点整合加以设计。
1.基于真实情境的数学课程相融性实施
基于真实情境的数学课程相融性主要表现在真实情境设置与数学教材的相互作用关系。学生一般对数学公式心存畏惧,尤其是数学公式的逻辑推理与求证过程。通过将抽象的数学公式与真实情境相结合,运用真实情境中的具体内容解释数学公式背后的逻辑,使学生的思维在具体与抽象之间架起一座桥梁。真实情境设置能使学生透过现象挖掘背后的本质,从而提高思维的深刻性。基于此,真实情境与数学课程相融合的设计思路如图3所示。
为此,“二元一次方程组的图像解法”课程内容相融性主要通过设计教学导入情境和3份带有真实情境问题的学习单作用于数学知识结构,建立有意义的联结。具体做法如下:
(1)为使学生产生有意义的联结,教师在上课前展示生活中的趣味情境,使情境与学生的认知结构相互作用。例如用来调节浴室中水供应的数学方程式,在统计学方程式的帮助下培育农作物,解释汽车开动时周围气体如何流动的纳维-斯托克斯方程(Navier-Stokes equations),卫星导航系统中涉及牛顿运动定律和万有引力定律等。通过这些情境设置使学生的学习内容与外在素材相融合。
(2)为了使学生更好地理解二元一次方程组的基础知识,设置篮球赛胜负比的真实情境,通过列算式、求根、绘图过程,理解数字背后的含义。利用真实情境中的数字信息解答数学公式背后的内在逻辑,将真实情境与数学知识更好地融合。
(3)通过设置商品组合的真实情境,将真实情境转化为直角坐标系中的图像,根据数学图像反过来求二元一次方程组相等解的情况。这样的设置将真实情境、直角坐标系及二元一次方程组表达式相融合。
(4)通过地铁周边土地地价之研判的情境背景材料,将真实情境转化为数学图像,根据直角坐标系找到最优解。此情境设置将数学知识结构与真实情境中的数学问题相融合。
2.教学要素转化
《义务教育数学课程标准(2022年版)》将学生的能力指标用“三会”来体现,即强调数学眼光、数学思维、数学语言对现实世界的重要性。[15]真实情境与现实世界相联系,无形中形塑学生能力指标,为此我们以初中数学的“二元一次方程组的图像解法”为例,按照转化需要具备的四个基本要素开发单元内容教材资源。通过学习,让学生知道在现实生活中存在着大量的线性方程问题,从而培养他们解决实际问题的能力。如表1所示。
表1中各案例根据转化四要素进行层层递进设计,以单元式知识内容为统领,将二元一次方程组的图像解法的知识贯穿始终。通过不同的真实情境,引导学生将数学知识与实际生活问题产生联系,建立信息联结,从而实现能力转化。知识要素围绕二元一次方程的列式、绘图,利用直角坐标系求根,判断根的情况,解决实际问题等进行内容呈现。情境要素围绕正向思维案例、逆向思维案例以及实际应用案例展开,促进学生将真实情境与数学知识相融合。表征内涵则充分利用数学工具,如语言文字、数学符号、图像等。智能活动围绕新课改的学习方式进行,以自主合作探究、竞赛展示、分组讨论等形式开展。四个要素相互渗透,彼此深化,从而有效实现从真实情境到学生能力的转化。
五、小结
真实情境与课程设计的相融性需要真实素材脉络与教材设计之间的相互作用,不论是数学工具的使用,还是资源开发,都离不开相互作用过程。把真实情境纳入数学教学过程,需注重真实材料和课程教材的关联性,需架起课程转化和能力指标实现的桥梁,即知识要素、情境要素、表征内涵、智能活动这四个要素的有机融合,实现学生由知识学习向能力转变。在这个转化过程中,知识呈现方式和问题解决模式直接决定着学习者对数学知识的理解程度,而认知风格又会影响学习者解决问题的策略选择。
根据奥苏贝尔有意义学习理论,学习本质上是将课本知识与现实生活建立有意义的联结。通过把真实情境嵌入学习者的知识脉络里,为学习者提供挑战真实世界问题的机会,他们不仅可以在情境中获得知识,而且学习也能从教室迁移到实践生活领域中。这种“回到教科书”式的课堂教学方式能够有效解决传统教学方式存在的诸多弊端,提高教学效率和质量,促进学生全面发展。基于此背景,本文提出真实情境学习模式。真实情境学习意味着将抽象的数学问题具体到对应的现实世界中,情境意味着通过特殊场景建构有意义的活动,进而完成知识与能力的转化。[16]课堂中的真实情境学习意味着创设一种现实环境,学生在体验现实世界中数学问题的复杂性和多样性的同时,会进行不断的经验改造、重塑和再创造,让数学与现实生活产生真正意义上的联结,从而真正做到运用数学眼光、数学思维和数学语言解释现实世界。
参考文献:
[1]FREUDENTHAL H. Revisiting mathematics education:China lectures[M]. New York:Kluwer Academic Publishers,1991.
[2]ROMBERG T A. Revisiting numbers:britannica mathematics in context[M].[S.l.]:Holt McDougal,2006:22-26.
[3]SHULMAN L S. Knowledge and teaching:foundations of the new reform[J]. Harvard educational review,1987(1):1-22.
[4]王有遠,欧阳园园,徐长斌.高职院校精品资源共享课程隐性知识转化研究[J].职教论坛,2018(10):55-60.
[5]梅景瑶,吕正则,朱凌.基于知识转化的工程人才创新能力提升研究:以一门综合创新实验课程的教学为例[J].高等工程教育研究,2018(1):159-164.
[6]GERICKE N,HUDSON B,OLIN-SCHELLER C, et al. Powerful knowledge,transformations and the need for empirical studies across school subjects[J]. London review of education,2018(3):428-444.
[7]周彬.教师教育专业知识:生成、积累与课程转化[J].教育研究,2021(7):37-47.
[8]李刚,吕立杰.落实学科核心素养:围绕学科大概念的课程转化设计[J].教育发展研究,2020(Z2):86-93.
[9]吕立杰,李刚.人才培养目标的课程转化路径探析[J].教育研究,2018(12):56-62.
[10]BROPHY J E. How teachers influence what is taught and learned in classrooms[J]. The elementary school journal, 1982(1):1-13.
[11]VOS P.“How real people really need mathematics in the real world”:authenticity in mathematics education[J]. Education sciences,2018(4):195.
[12]VERSCHAFFEL L,SCHUKAJLOW S,STAR J,et al. Word problems in mathematics education:a survey[J]. ZDM mathematics education,2020(52):1-16.
[13]仝玉婷,郑太年.美国EM教材数学情境设计及其对我国的启示:以EM教材中的“分数”内容为例[J].现代教育技术,2021(10):32-39.
[14]李玲,王宝霞,付惠.“思维可视化”在小学数学教学中的实践与思考[J].教育理论与实践,2021(35):57-59.
[15]唐彩斌,史宁中.素养立意的数学课程:《义务教育数学课程标准(2022年版)》解读[J].全球教育展望,2022(6):24-33.
[16]莱夫,温格. 情景学习:合法的边缘性参与[M]. 王文静,译. 上海:华东师范大学出版社,2004:43-47.
(责任编辑:潘安)

