以“问”启“智”，助推学力发展

薛龙跃

摘 要：促进学生学习力的发展在当下的数学课堂教学中十分重要.以“问”启“智”的数学课堂给了学生思考、猜想、探究、发现、验证和归纳的机会，充分展现学生的潜能，让学生的思维更活跃，更促进学生学习能力的提高，最终助推学习力的发展.

关键词：小学数学；思维生长；学习力

在素质教育纵深发展的当下，数学课堂越发注重师生的生命力价值，进一步从学生的立场着手反思，促进学习力的发展是数学课堂教学的重中之重.什么样的课堂是助推学生学习力发展的课堂呢？自然需要教师基于核心知识，通过问题串为学生搭建思维阶梯，激发和引导学生有智慧地数学思考，有效启迪学生学会思维，从而进一步提升其学习能力，最终助推学习力的发展［1］.下面结合教学实践提出以“问”启“智”的教学手段，夯实学习发展教学的过程.

1 用心设计引领“实践操作”的问题串，培养探究能力

数学课堂是充满创造机会的地方，这就需要教师以“问题串”为导引，激起学生的探究欲望，用开放的课堂设计，为学生提供创造的机会，让学生经历一次又一次探索与发现的过程，启迪学生在“做数学”的过程中，培养主动探究的意识，感受数学之妙，培养和提高学生的探究能力.

案例1：圆的认识

问题1：请你想出一个办法，帮助体育老师在操场上画出一个大大的圆.

设计说明：问题1的抛出，使得学生的探究欲望呼之欲出.学生从自身的已有生活经验出发展开思考，基于圆规画圆这一方法的经验，有的提出可以利用竹竿画圆，有的提出可以利用绳子画圆等.教师顺势拿出绳子想要与学生进行画圆的“较量”.学生不甘示弱，立刻与教师展开了比赛，结果自然教师获胜，学生画出起伏不定的“圆”.学生顿时不免产生疑问：为什么老师画的圆是标准的，我们画出的圆却不标准呢？就这样，学生的求知欲望被进一步激发.

问题2：教师借助绳子画出了一个标准圆，而刚才的两位同学为什么不能呢？

设计说明：這一问题的抛出，引发了学生浓厚的探究兴趣.学生再次回顾画圆的过程，立刻有学生提出：两种绳子不一样，我们是一种有弹性的绳子.就这样，学生从进一步思考和探索中明晰了“画圆不仅需固定中心点，绳子的长度也不可变化，这样绕中心点旋转一周才能画出一个标准的圆”.

问题3：独立观察，试一试找出圆中隐藏的其他秘密，并与同桌分享你的想法.

设计说明：随着问题难度的加大，学生逐步走上了探索之路.这一问题不仅可以引导学生回想圆的特点，并归纳得出圆的基本特征，还能积累画圆的活动经验，使得学生的思维经历具体到抽象再到具体的过程.

以上案例中，教师借助于生动活泼的实践操作，让学生亲历画圆的过程，自主体验和感悟圆的基本特征.整个过程中，引领性的语言和拾级而上的问题串使得学生的浅层次活动感受向着较高层次的活动经验逐步转化.就这样，将思维的深刻蕴藏在数学问题、操作活动和比赛之中，通过层层深入的提问让学生的探究能力与学习能力得到了有效发展.

2 用心设计引领“猜想验证”的问题串，培养推理能力

在课堂教学中，学生的“学”是核心，问题串导学不仅可以引发学生的数学探索，使其经历数学思考的过程，还能检验数学猜想的正确性，引领更深层次的推理探索，从而实现知识的深度建构［2］.因此，在教学的过程中，教师需从学生的思维水平和已有生活经验出发，设计引领“猜想验证”的问题串，引导学生深入观察和实践，推动数学归纳和类比，最终获得数学猜想.这样的过程，还有助于彰显个性化思维，实现知识建构和推理能力提升的目的.

案例2：三角形的分类

问题1：大家猜一猜，这个从信封中露出一个角的三角形是什么三角形？

设计说明：教师抛出的问题1从本质上来说是多个问题，若信封外露出的是一个直角或钝角，学生则可以较快地推导得出信封中的三角形.而当露出一个锐角时，学生的判断就容易出错了.这里，当教师拿着露出一个锐角的信封时，学生果然因思维定式给出了“锐角三角形”的错误结论.而片刻之后，大部分学生在反思后领悟过来，并重新给出猜想“可能是锐角三角形，也可能是直角三角形，也可能是钝角三角形”.教师进一步追问理由，学生从三角形角的特征出发，借助各种各样的策略进行了阐述和验证.就这样，学生也就完整地经历了一次演绎推理的过程.

问题2：倘若露出的锐角就是这个信封中三角形的最大的角呢？是什么三角形？为什么？

设计说明：教师进一步提出的问题2，又一次为学生提供了一些“说”的机会，并让他们在说理的过程中明晰“倘若三角形中最大的角是锐角，该三角形即为锐角三角形”.

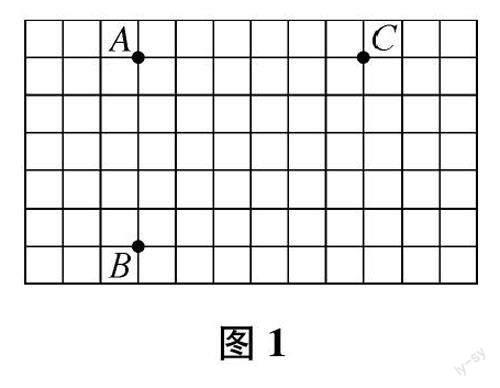
问题3：如图1，这个钉子板上的点A和点B是固定的，移动点C可以围成不同的三角形，仔细观察和思考，你发现了什么？

设计说明：问题3的抛出，为学生提供了一些“做”数学的机会，让他们在此过程中发现点C处在不同位置时围三角形的规律.

数学猜想不仅是一种技巧，也是一种能力，经历数学猜想的过程，可以更高效地激发学生的发散性思维，发展推理能力.以上案例中，问题串的设计在学生的认知结构基础之上，利用问题串引导学生猜想验证，在此过程中充分发挥学生的能动性，引导学生经历猜想、验证、讲理的过程，最终在问题解决的过程中提高学生的推理能力［3］.

3 用心设计引领“整理归纳”的问题串，培养梳理能力

整理归纳的过程也是对知识进行梳理的过程，更是助力学生建构知识网络的过程.当学生在思考问题串时，教师尝试让学生进行整理归纳，思维的过程随着问题的展开一步步深入.在这一过程中，学生能够对知识进行整理归纳，则可以在对知识的再发现和再认知中提升自身的梳理能力，充分建构完整的知识结构.

案例3 “多边形的面积”的整理与复习

问题1：回忆一下，学过的多边形面积计算公式有哪些？试着用你擅长的方式整理出来.

设计说明：问题1可以很好地帮助学生梳理单元知识，更重要的是达到了让学生反思知识点间联系的效果.之后，学生采用了不同方法进行整理，充分彰显了思维的多样性，同时也能在有序的思考和整理中很好地建构知识间的内在联系.

问题2：这些图形面积计算公式是如何推导的？在此过程中有何共同特征？

设计说明：回顾图形面积公式推导过程之后进一步引导学生归纳共性，这一过程可以让学生感受转化的作用，从而提升学生的理解水平.

问题3：哪个图形在转化的过程中更重要，为什么？

问题4：试着摆一摆黑板上的几个多边形，并阐述它们之间的关系.（具体图示略）

设计说明：问题3和问题4着重引导学生从图形的面积计算公式间的关联性出发，通过去说、去摆、去理等“做”数学的方式，直观归纳图形面积计算公式间的关系，促进学生形成自己的知识体系.

复习课相对于新授课而言难度较大，需要我们以问题串创设自如的课堂环境，让学生在整理归纳中建构知识体系.以上案例中，教师从数学知识的特点出发设计问题串，让学生去整理归纳，从而将单一的、零碎的知识连线织网，促进知识体系的建构，同时培养学生的梳理能力.

总之，在数学教学中，基于学生认知结构的问题串设计，探寻到了课堂教学的真实起点，有效把握住了学生思维发展的生长点，引领学生去思考、去探索、去实践、去归纳、去猜想、去建构.这样的问题串设计根植于学生，更能够让学生踏阶而行，培养探究能力、推理能力和梳理能力，大大地提升数学学习力.

参考文献：

［1］ 兰爱爱，吴利敏.数学核心素养在初中课堂教学中的培养途径探析［J］.湖州师范学院学报，2018（8）：111-116.

［2］ 管明贵.精心设计问题串，提高课堂教学效益［J］.数学大世界（中旬），2017（4）：3.

［3］ 孙军.问题链教学在初中数学教学中的运用分析［J］.新校园：中旬刊，2015（8）：115.