判别性增强的稀疏子空间聚类

胡慧旗，张维强，徐晨

（深圳大学 数学与统计学院，广东 深圳 518060）

0 概述

子空间聚类是一种非常有效的高维数据聚类方法，假设高维数据分布在几个低维子空间的并中，其目的是将高维数据分成不同的类，一类对应一个子空间。目前，子空间聚类已被广泛应用于计算机视觉［1］、图像处理［2-3］、系统识别［4］等领域。基于谱聚类的子空间聚类算法因其计算简单、聚类性能优异而成为研究热点。稀疏子空间聚类（SSC）［5-6］、低秩表示子空间聚类（LRR）［7-8］和最小二乘回归子空间聚类（LSR）［9］是基于谱聚类的子空间聚类中3 个经典的算法，它们的共同点是利用高维数据的自表示构建相似度矩阵，然后通过谱聚类得到聚类结果。3 种算法的不同点在于自表示系数的约束不同：SSC 对自表示系数矩阵采用l0或l1范数约束，希望每个数据的自表示是稀疏的，仅被其所属子空间（即同类）的数据表示，但是稀疏约束会导致自表示过于稀疏，即仅从同类数据中挑选最相似的数据对其表示，忽略了其他相关的数据，不利于聚类；LRR 对自表示系数矩阵采用低秩约束，这是一种全局结构，但低秩表示可能导致过于稠密的自表示，即不同子空间的数据参与了表示，另外，当数据采样不足时，低秩表示可能会失效；LSR 对自表示系数采用l2范数正则，这有利于将高度相关的数据聚集在一起，但也会导致类内类间的自表示都是均匀的，不利于分离不同类别的数据。

在子空间独立的条件下，以上3 种算法都被证明自表示系数矩阵是一个分块对角矩阵，即来自不同子空间数据间的表示系数为零。自表示系数矩阵的块对角结构揭示了数据与低维空间的真实隶属关系，从而相应相似度矩阵表现出类内相似度高、类间相似度低的特性，这有利于谱聚类产生正确的聚类标签。因此，子空间聚类问题关键在于自表示系数矩阵的构造，理想的自表示系数矩阵应同时具有稀疏性和聚集性，即类间稀疏、类内聚集。鉴于这一考虑，很多算法［10-12］对数据的自表示矩阵同时进行稀疏约束和低秩约束，或者同时进行稀疏约束和l2范数约束，强制自表示系数矩阵具有稀疏性和聚集性。FENG等［13］指出自表示系数矩阵应具有块对角结构，并通过添加显式的硬约束，强迫SSC 和LRR 得到的自表示系数矩阵具有精确的块对角结构。进一步地，LU等［14］提出K块对角正则项，迫使自表示系数矩阵具有块对角结构。考虑模型的整体性能，LI等［15］提出结构稀疏子空间聚类（SSSC）模型，通过引入联合正则项实现系数矩阵和聚类标签的联合学习，使得模型直接输出聚类标签。受SSSC 模型启发，ZHANG等［16］在LRR 模型中加入联合正则项，提出低秩结构稀疏子空间聚类（LRS3C）模型，构建了一个联合优化框架。在LRS3C 基础上，YOU等［17］通过添加促使低相关数据尽量远离的l1范数正则项，防止系数矩阵过于密集，加强了类间数据的稀疏性，进一步提升了聚类性能。

然而，原始数据中往往存在噪声和其他干扰，直接对原始数据进行自表示得到的相似度矩阵也会受到噪声或干扰的影响，导致不能准确反映数据的真实子空间隶属关系，造成数据误分类。针对此问题，SRR［18］对原始数据进行了二阶自表示：首先对原始数据进行自表示，由于得到的自表示矩阵反映了每个数据与其他数据的某种相关性，因此称其为邻域关系矩阵；然后将每个数据的自表示向量作为数据的新特征，对新特征再进行二阶自表示，也称为重构系数矩阵；最后基于此矩阵构造相似度矩阵，并通过谱聚类得到最终聚类结果。实验结果表明，该方法具有较高的聚类精度。

本文基于SRR 中数据的邻域关系可准确反映数据类别属性这一特点，提出一种兼顾相似度矩阵稀疏性和聚集性的子空间聚类方法。利用F 范数代替核范数，降低SRR 模型的求解难度，并构建一个新的正则项来增强不同类别数据之间表示系数的判别性。在此基础上，使用人脸和手写体数字数据集进行实验，验证本文方法的聚类效果。

1 符号定义与相关工作

考虑到原始数据中存在大量噪声和干扰，WEI等［18］认为数据间的邻域关系特征比原数据更能揭示其类别属性，并提出如下SRR 模型：

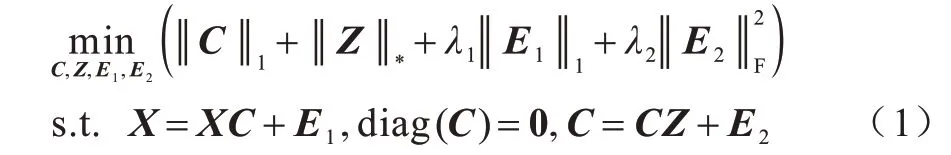
其中：X表示原始数据矩阵，其中一列对应一个数据样本；C为邻域关系矩阵；Z为重构系数矩阵；用于刻画数据中的离群点；用于处理邻域关系矩阵中的高斯噪声；λ1和λ2为权重参数。在SSR 模型中：首先邻域关系矩阵C的每一列表达了原始数据矩阵X中的对应列与其他数据之间的某种相关性，并利用l1范数对其进行约束；然后将C作为原始数据X的新特征进行自表示或自重构，用核范数来约束重构系数矩阵Z；最后用Z计算相似度矩阵，并通过谱聚类得到聚类结果。实验结果表明，该模型能够显著提升子空间聚类性能。

本文在SRR 模型基础上进行改进，提出一个新的模型，并给出求解算法。

2 判别性增强的稀疏子空间聚类模型

2.1 模型构建

文献［19］中证明，在一定条件下，基于F 范数的表示和基于核范数的表示是等价的，而平方F 范数最小化问题不需要矩阵奇异值分解运算。因此，本文利用平方F 范数代替SRR 中的核范数，使模型易于求解。F 范数能够保证重构系数矩阵Z的类内一致性，但是不能保证类间判别性，而C的l1范数有利于保证C的类间判别性，不能保证类内聚集性。因此，本文引入新的正则项来保证Z的类间判别性和C的类内聚集性。实际上有两重作用：当C给定时，若Ci、Cj不相似，即较大，则该正则项有利于使Zij接近于0，从而两个对应数据的相似度较小，有利于将其分为不同类；反之，当Z给定时，若两个数据的相似度|Zij|较大，则该正则项有利于使新特征Ci、Cj相似，从而保证特征的类内聚集性。

综上，本文给出以下改进的SRR 模型：

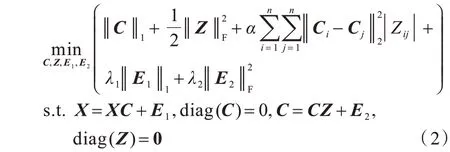
其中：α是权衡参数；diag(Z)=0 防止出现平凡解。

2.2 模型求解

本文采用交替方向乘子法（ADMM）［20-21］求解式（2）模型，引入辅助变量J和P，使模型转变为：

式（3）模型的增广拉格朗日函数表示为：

其中：Y1、Y2、Y3、Y4是拉格朗日乘子；μ1、μ2、μ3、μ4是惩罚项。交替更新J、C、Z、P、E1、E2、Y1、Y2、Y3、Y4，更新一个变量的同时固定其他变量的值。

固定其他变量，关于J的子问题为：

利用软阈值算子求解式（5），得到J的解为：

固定其他变量，关于C的子问题为：

式（9）是关于C的二次函数，其最优解满足以下方程：

式（10）是一个标准的Sylvester 方程，可以通过Matlab 的lyap 函数解决。

固定其他变量，求解下列问题更新Z：

对变量Z量求导并令其为0，Z的闭式解如下：

式（13）可以通过软阈值算子求解：

固定其他变量，更新E1即求解：

根据软阈值算子可得E1的解为：

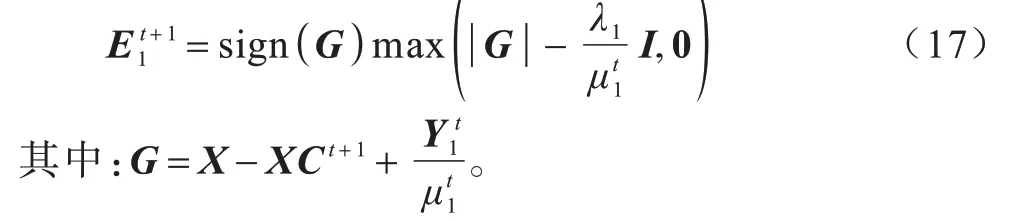
固定其他变量，更新E2即求解：

变量E2的解为：

更新拉格朗日乘子：

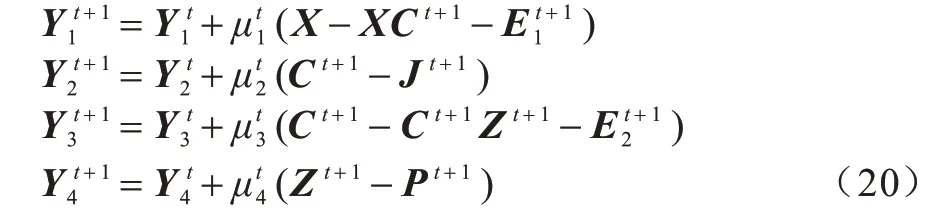
以上给出了利用ADMM 求解式（3）问题的各个变量的迭代公式。基于上述分析，给出以下迭代算法：

输入数据矩阵X，类别个数k，权衡参数α、λ1、λ2

输出聚类标签

2.3 计算复杂度分析

本文算法中更新变量J、Z、P、E1、E2的计算复杂度均为O(n2)，更新式（10）中邻域关系矩阵C需要求解Sylvester方程，其计算复杂度为O(n3)，因此，算法总的计算复杂度为T1×O(n3)，其中T1为迭代次数。由文献［18］可知，SRR 的计算复杂度为T2×O(n3)，其中T2代表迭代次数。通过对比发现，本文模型求解算法和SRR 模型求解算法的计算复杂度均为3阶。

3 实验

在经典数据集Extended Yale B［23］、ORL［24］、USPS［25］和MNIST［26］上进行实验来验证本文方法的有效性。同时，将本文模型与SSC［6］、LRR［7］、LSR1［9］、LSR2［9］、SSSC［15］、BDR-B［14］、BDR-Z［14］和SRR［18］模型进行比较。使用聚类错误率作为性能评价指标，其定义为误分类数据点个数与数据点总数的比值。聚类错误率越小，表示误分类的数据点越少，聚类效果越好；反之亦然。

本文实验在Intel®CoreTMi7-9700 CPU@3.00 GHz处理器配置下，Matlab R2018b 环境中进行。

3.1 参数分析

本文模型包含3 个权衡参数：α，λ1，λ2。参数α的取值越大，不同类别数据之间的自表示系数越小；参数λ1的取值大小决定了对原始数据奇异点进行处理的程度，设置适当的参数λ1，可以有效去除数据样本中的噪声，减小噪声对获取数据的新特征的影响；参数λ2用于进一步去除数据的新特征中的噪声。在Extended Yale B上，各参数对聚类结果的影响如图1所示。

图1 Extended Yale B 数据集上聚类错误率随参数的变化Fig.1 Clustering error rate versus parameters on Extended Yale B dataset

图1（a）是固定α=0.005，聚类错误率随另外2个参数变化的柱形图。可以看出，本文模型的聚类错误率主要取决于参数λ1，当λ1=0.5时，参数λ2取{0.001，0.005，0.01，0.05，0.1，0.5，1}中的任意值，聚类错误率都处于较低水平，这表明相较于第2次自表示中的噪声处理，第1次自表示对原始数据的噪声适当处理更为重要。

图1（b）是固定λ1=0.5，聚类错误率随另外2个参数变化的柱形图。可以看出，当α=0.001或0.005时，本文模型的聚类错误率较低，λ2取{0.001，0.005，0.01，0.05，0.1，0.5，1}中何值对聚类错误率影响不大，这表明本文提出的正则项对聚类性能起到重要作用。

综上可知，当α=0.005、λ1=0.5、λ2=0.001时，本文模型的聚类错误率最低，因此，将此组参数值作为参考经验最优参数。

3.2 人脸数据集实验

本节为选用Extended Yale B 和ORL 数据集的实验结果与分析。图2（a）和图2（b）分别为Extended Yale B数据集和ORL 数据集的部分人脸图像。

图2 Extended Yale B 与 ORL 数据集部分人脸图像Fig.2 Some face images of Extended Yale B and ORL datasets

Extended Yale B人脸数据集包含38个人的2 414幅人脸图像，其中每人约有64幅不同光照和姿势下的人脸图像。对于Extended Yale B数据集，本文遵循文献［27］中的数据处理过程：1）将每幅图像下采样到48×42 像素；2）将38人分为4个小组：1～10，11～20，21～30，31～38，对每组考虑2、3、5、8 个不同人的人脸图像的所有组合，对前3 组的每组考虑10 个不同人的人脸图像的所有组合。在此数据集上，SSC、LRR、LSR1、LSR2 和SSSC 模型的聚类错误率数据参考文献［27］。对BDR-B、BDRZ、SRR 和本文模型，通过选择参数以达到最低的聚类错误率，然后计算所有实验中聚类错误率的平均值、中值和标准差。

ORL 人脸数据集包含40 人在不同时间、光照、表情、角度、是否配戴眼镜等环境下拍摄的400 幅人脸图像，其中每人有10 幅人脸图像。对于ORL 数据集，考虑到降低计算时间和复杂度，本文将每幅图像下采样到32×32 像素。在此数据集上，调节参数使得模型效果达到最优。

各模型在Extended Yale B 和ORL 数据集上的聚类错误率如表1 所示，其中加粗表示最优值。

表1 各模型在Extended Yale B 和ORL 数据集上的聚类错误率 Table1 Clustering error rate of each model on Extended Yale B and ORL datasets %

由表1 可以看出，本文模型在2 个人脸数据集上均实现了比其他模型更低的聚类错误率。虽然所有模型的聚类错误率随着类别数目的增加都呈升高趋势，但其他模型迅速升高，而本文模型增高幅度较小，聚类错误率稳定在2%以内，标准差也稳定在1%以内，表明随着类别数目的增加，当聚类问题更具有挑战时，本文模型更加鲁棒。ORL 人脸数据集具有强非线性结构，对聚类方法提出了更大的挑战，但本文模型依旧实现了较对比模型更低的聚类错误率，聚类性能更优。为了更直观地对比不同方法，在Extended Yale B 数据集上，根据表1 的结果绘制了折线图，如图3 所示，从中可以明显看出，本文模型的聚类错误率始终低于其他对比模型。

图3 Extended Yale B 数据集上平均聚类错误率与类别数目的关系Fig.3 Relationship between average clustering error rate and number of subjects on Extended Yale B dataset

3.3 手写数字数据集实验

USPS 和MNIST 是2 个常用的手写数字图像数据集，USPS 和MNIST 均包含0～9 这10 个类别手写数字图像，部分图像如图4（a）和图4（b）所示。

图4 部分手写数字图像Fig.4 Some handwritten digital images

USPS 数据集包含9 298 幅手写数字图像，每幅图像的尺寸为16×16 像素。在此数据集上，利用每个手写数字的前100 幅图像进行实验，则可得到256×1 000 的数据矩阵。在MNIST 数据集上，取训练集每类手写字的前100 幅图像。考虑到算法运行时间，将每幅图像下采样到28×28 像素，展开为一个784 维的向量，此时数据矩阵的大小为784×1 000。

各模型在USPS和MNIST数据集上的聚类错误率如表2所示，其中加粗表示最优值。可以看出，本文模型的聚类错误率远小于其他模型，聚类性能最优。

表2 各模型在USPS 和MNIST 数据集上的聚类错误率 Table 2 Clustering error rate of each model on USPS and MNIST datasets %

3.4 运行时间对比

各模型在4 个数据集中指定数据上的运行时间如表3 所示。可以看出：统一模型SSSC 花费时间最多；LSR 模型（包括LSR1 和LSR2）花费时间最少；本文模型和SRR 模型虽然都具有3 阶计算复杂度，但本文模型在4 个数据集上的实际运行时间均少于SRR 模型。

表3 各模型在4 个数据集上的运行时间 Table 3 Runtime of each model on four datasets 单位：s

4 结束语

本文对SRR 模型进行改进，首先用平方F 范数取代核范数，避免核范数求解需要的奇异值分解，并获得解析解；然后引入类别属性增强的正则项，提高不同类别数据的自表示系数的判别性。在多个人脸以及手写数字数据集上的聚类结果表明，本文改进模型的聚类性能优于SSC、LRR、SSSC 等对比模型。下一步将考虑算法的收敛性，将模型扩展应用于多视角数据的子空间聚类问题。