基于茫然传输协议的FATE 联邦迁移学习方案

郑云涛，叶家炜

（1.复旦大学 计算机科学技术学院 上海市智能信息处理重点实验室，上海 200433；2.复旦大学 计算机科学技术学院 教育部网络信息安全审计与监控工程研究中心，上海 200433）

0 概述

近年来，由于数据的存储与处理效率的提高，海量数据参与机器学习模型的训练成为可能。利用不同来源的数据进行机器学习模型训练并生成预测模型能够获得更多的特征信息，从而提高模型的预测准确率。然而，现实中大多数数据分散在不同的组织中，由于受到法律等的约束，无法通过集成来进行共同的机器学习模型训练，如医院的患者信息、银行的用户账户信息等数据并不能得到公开共享，这使得整合来自不同来源的数据比较困难。因此，数据的隐私保护技术成为大数据时代机器学习不可或缺的技术手段。

安全多方计算是一种能够在保证计算参与方的数据不被泄露的情况下完成最终计算过程的隐私保护技术。目前，研究人员提出了多个实现安全多方计算的协议，包括利用同态加密来直接对数据进行加密的协议［1］、利用秘密共享实现数据不被泄露的Shamir 秘密共享方案［2］、茫然传输（Oblivious Transfer，OT）协议［3］等，以及相关的秘密分享协议框架，如SPDZ 协议［4］、ABY 协议［5］等。

联邦学习利用安全多方计算技术来对机器学习模型中的数据进行保护，在不泄露用户数据隐私的情况下共享数据并构建机器学习模型，使得训练出的模型的预测准确率不会受到损失。目前联邦学习的隐私保护机制的实现有基于模型聚类［6-8］、基于同态加密［9-11］、基于差分隐私［12］以及基于秘密分享［13］等相关研究。

FATE 联邦学习是一个成熟的、已投入使用的基于同态加密的联邦机器学习框架，文献［14］提出的FATE 联邦迁移学习框架，通过近似多项式的方法来拟合逻辑回归函数，并用Paillier 同态加密［15］的方式，在保证参与联邦学习双方的数据隐私的情况下完成损失函数和梯度的计算，最终达到收敛完成模型的训练。然而，由于在实际的模型训练过程中需要对大量的数据进行加密处理和计算，模型训练的效率较低。文献［16］提出了通过批量加密的方法来提高同态加密的通信效率，但是本质上没有解决同态加密乘法的计算开销问题。

针对FATE 联邦迁移学习（Federated Transfer Learning，FTL）中同态加密带来的计算开销的问题，本文提出一个基于OT 协议的隐私保护两方矩阵运算方案，并拓展应用到FATE 联邦迁移学习的设计中，在保证参与计算双方的数据隐私的前提下完成逻辑回归模型的损失函数和梯度计算。同时，针对OT 协议带来的通信开销问题，通过OT 扩展（OT extension）协议和批量传输进行优化，实现基于OT协议矩阵运算的FATE 联邦迁移学习方案。

1 预备知识

1.1 联邦迁移学习

联邦学习最早由谷歌在2016 年提出［17］，目的是通过分布在不同设备上的数据集来协同构建机器学习模型，并防止各个设备的数据泄露。

假设有n个数据持有组织{p1，p2，…，pn}，每个组织拥有自己的数据Di（1 ≤i≤n)，通过中间数据的交互来共同训练机器学习模型Mfed。一种常规的联合机器学习方法是将所有组织的数据聚合在一起，共同训练模型得到模型Msum。与普通的联合机器学习不同，联邦学习各个组织的数据Di不会泄露给其他组织。根据Vfed和Vsum联邦学习与联合学习的准确性，假如|Vfed-Vsum| ＜δ，则称该联邦学习算法有δ-acc级损失。

联邦学习的分类有横向联邦学习、纵向联邦学习与联邦迁移学习。横向联邦学习适用于样本不同的情况下参与方数据集的特征空间相同的情况；纵向联邦学习适用于参与方样本空间重合度高，但各自的特征空间不同的情况；如果参与方之间的数据的特征空间和样本重合度都很低，则需要用到联邦迁移学习，如图1 所示。

图1 联邦迁移学习框架Fig.1 Framework of federated transfer learning

1.2 OT 协议

OT 协议是重要的密码学原语之一，在实际应用中，往往需要许多简单的协议来完成高级协议的设计，在执行k次的协议（记为kO）中，发送方S持有k对比特对(，mi1)，其中，∈{0，1}，而接收方R持有一个k比特的选择向量b，通过执行k次协议后，R获得了，但是无法得知其他的比特位信息，而S无法得知b的信息，从而保证了隐私性与保密性。目前研究人员提出许多高效的OT 协议方案，如在半诚实模型下通过公钥机制来实现的Naor-Pinkas OT 协议［18］等。

OT extension 协议利用少数的Base OT 协议将原本大量的OT 协议数量大幅减少，能够极大地降低计算量和通信量。IKNP OT extension 协议［19］通过选定安全参数k，能够将m次协议降低到k次的Base OT 协议。发送方准备m对秘密消息作为协议的输入，接收方准备{0，1}m比特对消息作为协议的输入。在协议执行过程中，双方在预处理阶段执行k次的Base OT 协议，发送方作为Base OT 的接收者，接收方随机产生k比特对消息作为Base OT 的发送者。执行完k次Base OT 协议后，双方即可以在交互阶段进行m次的协议的交互，而每次协议的执行只需要进行少数的异或运算。接收方最终会获得自己选择的m个消息。IKNP OT extension 不仅能够减少OT 协议的通信量，也加快了计算效率。

1.3 逻辑回归的泰勒展开近似

在线性回归模型中，模型训练本质上是需要拟合出一条线，使得训练样本中的数据点尽可能多地靠近这条线，即y=W·x，其中：W是要训练的模型参数，它通过随机化一个初始值得到；x为参与训练的样本数据，它可以是一个向量，也可以称为特征值；x与W的维度大小是相同的，y是一个单值，也可以称为标签。

为了能够学习到模型的参数W，一般采用损失函数Loss 和随机梯度下降的算法来更新每一轮的W。Loss 函数为均方误差，计算公式如下：

无论是Loss 函数还是梯度计算，式（1）、式（2）都只涉及乘法和加法运算，因此可以使用多方安全计算来直接运用到线性回归问题上，同态加密与秘密分享的方法都是可行的，然而对于逻辑回归等模型的损失函数的计算，往往需要用多项式近似的方法来模拟损失函数［20-22］。文献［11］利用二阶泰勒展开的方式近似模拟损失函数并给出了精度损失的比较。对于损失函数：l1(y，φ)=loga(1+exp (-yφ))，其中，φ为训练模型的预测值，其二阶泰勒展开式为：

采用二阶的泰勒展开作为逻辑回归的损失函数拟合进行模型的训练。

2 基于OT 协议的矩阵运算设计

设计一种基于OT 协议的多方安全计算方案，并将其应用到矩阵乘法运算。

2.1 基于OT 协议的整数乘法运算

将OT 协议在比特位上的与运算扩展到简单的整数乘法运算，假设需要计算a·b，其中，A 持有a，B持有b，则：

2）B 作为OT 协议中的秘密提供方，随机化整数c，将c与c+b作为OT 协议的输入。

3）A 作为OT 协议中的选择方，输入为ai，输出结果为aib+c，即：当ai=0时，输出为c；当ai=0时，输出为c+b。

2.2 基于OT extension 协议的安全矩阵运算

构造基于OT extension 协议的矩阵运算的多方安全计算方案。

对于矩阵A和B的运算，P1拥有矩阵A，P2拥有矩阵B，针对矩阵运算分别进行如下构造：

1）A+B

对于需要相加的所有原矩阵或秘密分享矩阵，P1和P2直接本地相加即可。

2）A×B（矩阵A与B的按位运算）

P1和P2对于矩阵中的每对元素乘法分别执行基于OT 协议的乘法运算，并对所有的协议通过OT extension 进行优化。

3）a＊B（矩阵的数乘）

A×B的特殊形式，但是由于每次乘法的都是同一个数，相当于每次协议的选择都一致，因此通过算法1来优化OT extension的输入。P1通过调用Batch（C）与Batch（C+B）得到OTInput，OTInput作为OT extension 的输入，P2转化整数，将cchoice=∪ {ai}作为OT extension 的输入。P2将收到的OTOutput或OTOutput反向解码回矩阵，执行基于OT 协议的整数乘法运算。

算法1OT 协议批处理算法Batch

在上式中，m为矩阵数的比特长度，Eij定义如下：

P1构造长为M=n×l×m的选择向量cchoice=∪ {aijk}作为OT extension 协议的输入。

②P2根据矩阵整数的比特长度m与矩阵An×l的大小生成相应的随机矩阵组Cr，1 ≤r≤m×n×l。

③P2将ssecret={(Cr，Cr+B)}作为OT extension 协议的输入。由于对于每个矩阵内元素的协议选择都是一致的，因此可以通过运行算法1，将矩阵中的元素进行合并得到OTInput，OTInput输入到OT extension 框架中，以此减少需要进行的协议数量，提升OT extension 的运行效率。

（2）交互阶段

①双方根据输入运行OT extension 协议，得到各自的输出。

②P1作为协议的输入方，得到批处理的矩阵输出OTOutput ＜Cr＞，OTOutput ＜Cr+B＞反向解码回矩阵得到RReceived：

由于联邦学习中涉及大量矩阵运算，本文提出的基于OT 协议的矩阵算法不仅能够大幅减少OT 协议执行的数目，而且通过OT extension 将所要处理的OT 协议数目进一步减少，从而提高了数据的运行效率。

3 基于OT 矩阵乘法的FTL 方案设计

如图2 所示，模型包括两个参与方A 与B，共同进行机器学习的模型训练，每个参与方的样本数量为n。主要由以下3 个部分组成：

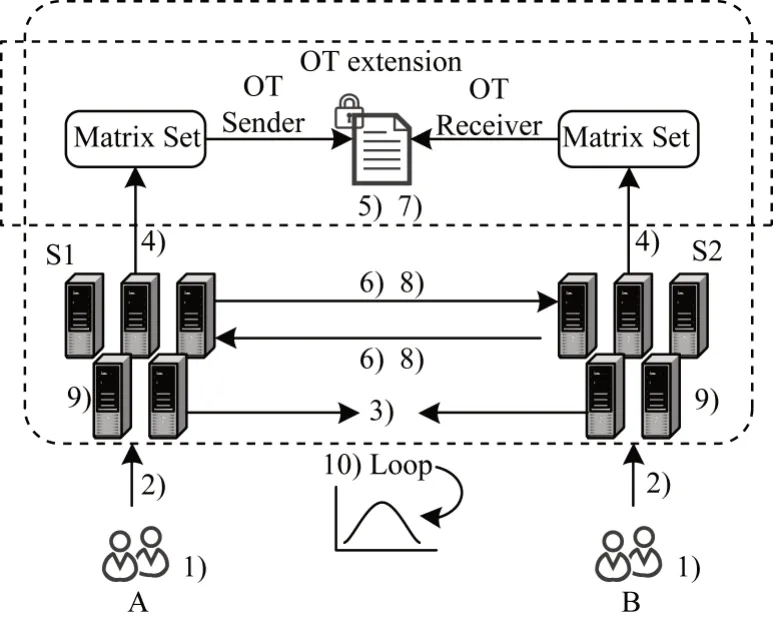
图2 基于OT 协议联邦迁移学习框架Fig.2 Framework of federated transfer learning based on OT protocol

1）参与方A 拥有一定数量n的样本，每个样本只有对应的特征值Xai=(xai1，xai2，…，xail) 和标签Yai，(Xai，Yai)∈DA。参与方B 拥有一定数量m的样本，每个样本只有对应的特征值Xbi=(xbi1，xbi2，…，xbil)，Xbi∈DB。DA与DB有少量的重合样本DC。假设A、B事先知道重合的样本ID，否则可以用RSA 加密机制对样本ID 进行盲化，然后进行样本对齐［6］。

2）A 和B 各自拥有的机器学习模型训练服务器S1、S2，这两个服务器各自受控于A 与B，不能进行共谋攻击。该服务器只负责机器学习模型相关的计算，如特征值计算、梯度计算、损失函数计算等。

3）OT 协议矩阵运算框架负责对计算出来的特征值进行信息的批量处理，并进行矩阵的安全计算。

假设参与方之间的通信存在安全通信信道，且双方的消息具有可验证性，图2 中的步骤标识对应流程如下：

1）A 与B 作为机器学习模型的参与方，在每一轮迭代中初始化各自模型的参数WA、WB。

2）A 与B 将本地的样本数据和初始化参数传输到机器模型训练服务器S1 与S2。

3）S1 与S2 通过RSA 加密机制盲化样本ID，进行样本对齐（可选）。

4）A 与B 用各自计算模型的特征值uA、uB，输入OT 协议框架准备进行安全矩阵运算。

10）返回步骤4），直到模型收敛。

定义1（安全性假设）当A、B 参与方都是半诚实模型时，任何恶意敌手可能且仅可能控制其中一方，则对M 有(OA，OB)=M(IA，IB)，其中，IB、OB是B的输入和输出结果，IA、OA是A 的输入和输出结果。假设A 是被恶意方控制的，如果对于任意数量的（，)，都有对应 的(OA，O′B)=M(IA，)，即恶意敌手无法分辨输出结果与随机结果，则该方案是安全的。

3.1 系统初始化阶段

假设OT extension 的安全参数为κ。

Setup(WA，WB，κ)→(∪r，∪s，∪K)

1）服务器S1、S2 根据输入的模型参数确定矩阵运算的维数，确定OT extension 需要进行的协议数量：m←（WA，WB)。

2）服务器S2 作为OT extension 协议的接收方，对于每个待计算矩阵，产生m维向量r=(r1，r2，…，rm)，rj∈{0，1}，1 ≤j≤m，作为自己的选择，初始化向量r的集合∪r。

3）选择Base OT 的数目κ作为安全参数。

4）发送方产生κ个随机数作为Base OT 的选择消息，s=(s1，s2，…，sκ)，si∈{0，1}，1 ≤i≤κ，初始化向量s的集合∪s。

5）接收方产生κ对随机数作为Base OT 的发送消息：，初始化向量K的集合∪K。

3.2 模型训练阶段-计算损失函数

Train1(WA，WB，DA，DB，DC)→L：

3.3 模型训练阶段-计算梯度

1）假设损失函数L 值并没有收敛，则需要计算对应的梯度值，根据式（4）得到：

计算得到梯度相关的分享值：3.2 节步骤2，重新计算损失函数。

4 安全性性能分析

4.1 安全性

定理1在半诚实模型假设下，两方的OT 矩阵运算方案是安全的。

证明在半诚实模型的条件下，参与矩阵运算的双方P1、P2是遵守协议规则的，但尝试去获取更多相关的信息。假设存在某敌手Adversary，每次最多只能控制P1、P2其中的一个。不失一般性地，假设对于矩阵的乘法B·A：当Adversary 控制A持有者作为OT 协议的接收方时，发送方每次执行OT 协议都会根据矩阵整数的比特长度m与矩阵An×l的大小生成相应的随机矩阵组Cr，1 ≤r≤m×n×l，以Cr+B与Cr作为输入，敌手或另一方服务器看来都是随机值的矩阵对，不会暴露任何有效信息；当Adversary 控制B持有者作为OT 协议的发送方时，选择方的选择隐私性依赖于OT 协议的安全性，在半诚实模型下是安全的，不会暴露自己的任何比特位信息。矩阵的按位乘法和数乘都将转化为基于OT 的乘法运算。同理，发送方每次执行OT 协议都会对应地产生随机数c，以c和c+b作为输入，在攻击者看来都是无法分辨的随机数。因此，对于任意一个矩阵运算，对于诚实方的任意Input，另一方接收到的Output 都是与随机值不可区分的，因此基于OT 协议的两方矩阵运算是安全的。

4.2 隐私性

定理2在半诚实模型安全性假设下，基于OT协议的联邦迁移学习方案不会暴露任何参与方的隐私信息。

证明在半诚实模型假设下，由于关于损失函数与梯度的计算都是基于OT 协议的矩阵运算构造方案，在矩阵运算的过程中不会暴露任何参与运算的数据的信息，因此可以推出：首先，对于恶意敌手Adversary，其在所有矩阵相关的运算中无法获得原始矩阵的任何信息；其次，对于最终传输的结果都是经过运算后的中间结果，并不会对A 与B 的数据特征信息uA与uB造成泄露；最后，这些中间结果都是由不同矩阵乘法或加法得到的累加值，在外部看来只是1 个随机的值，而不是某2 个矩阵直接相加或相乘得到的结果，即使在A 或B 重建恢复出这些中间结果之后，也不能反推出相应的模型参数值或数据特征信息。

在半诚实模型下的每一轮迭代中，A 或B 只能学习得到自己对应的梯度值或损失函数值，以此更新自己的参数，即对于任意数量的诚实方的输入，Adversary 无法得到与诚实方的输入相关的任何信息。

4.3 可扩展性

FATE 联邦迁移学习方案在效率优化和应用上都有很好的扩展性。

首先，在矩阵运算效率的提升方面，构造了线上的基于OT 协议矩阵乘法运算，可以对应地在线下构造大量的乘法三元组来进行优化［23-24］，构造乘法三元组的过程可以作为预处理输入，从而增加线上的效率，具有很高的实际应用意义。

其次，对于应用上的扩展，构造了逻辑回归机器学习模型的训练方案，而简单神经网络的每一层的激活函数与逻辑回归类似，在二分类的问题上，可以拓展应用到神经网络的拟合中，从而实现更高精确度的机器模型训练方案［13，25］。

4.4 效率分析

在局域网环境下基于FATE 联邦迁移学习框架代码进行了实现，运行机器是Intel 5220R 2.2 GHz 的CPU 处理器，为24 核48 线程以及128 GB RECC DDR4 内存，环境为64 位的Ubuntu20.04。实验使用C++语言编写IKNP OT extension 库并通过批量处理优化效率，通过extern C 关键字由C 语言编译成动态库libOTE.so 供机器模型训练代码使用。同时，逻辑回归模型训练采用Python 语言以及numpy 库进行编写。

表1 本文方案与FATE 联邦迁移学习方案性能对比 Table 1 Performance comparison between proposed scheme and FATE federated transfer learning scheme

图3 所示为本文方案在不同特征维度下的收敛时间变化与同态加密方案的联邦迁移学习方案的比较，实验模拟方案的样本数量为500个，样本重合数量为50个。可以看出：在特征维度增加的条件下，本文方案的时间开销呈线性稳定增长，依然拥有较好的性能稳定性，且平均效率比基于同态加密的FATE 联邦迁移学习方案高25%左右。可见本文方案在较为复杂的样本类型中仍然具备较好的性能，具有一定的实际应用意义。

图3 不同特征维度下的联邦迁移学习收敛时间Fig.3 Convergence time of federated transfer learning under different feature dimensions

5 结束语

本文提出一种基于茫然传输协议的安全矩阵计算方案。通过实现矩阵的加法、乘法与数乘的安全运算，完成逻辑回归模型的损失函数与梯度更新的计算，并将其嵌入到FATE 联邦迁移学习的框架中。同时，通过OT extension 技术和通信批处理计算，减少矩阵运算所需的OT 协议的通信开销。实验结果表明，与同态加密的方案相比，本文方案能够有效提高FATE 联邦迁移学习框架中模型的收敛效率。下一步将研究拓展本文方案在多方机器学习模型上的训练，以及通过乘法三元组结构来进行线下的预处理，从而提高线上的效率。