对与圆锥曲线切线有关的一个定值的证明

刘大鹏

(辽宁省黑山县第一高级中学 121400)

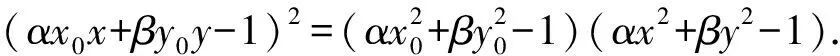
引理2 自抛物线y2=2px(p>0)外一点P(x0,y0)引抛物线的两条切线的方程为

1 对与双曲线切线有关的一个定值的证明

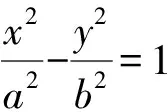
证明因为切线l1,l2的方程分别为

根据引理1，过点A(x′,y′)的切线方程为

=0.

联立直线DE的方程和双曲线的方程，

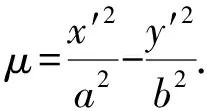
所以结论成立.

所以双曲线上的点(x0,y0)满足

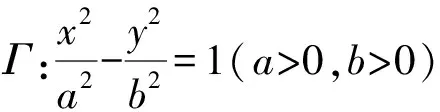
图1

证明记过点A的两条切线分别与双曲线相切于D，E两点，设A(x′,y′),D(x1,y1),E(x2,y2),F(x0,y0),因为点A在直线l上，所以点A的极线DE必过直线l的极点，坐标记为(m，n).

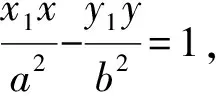
因为a2(y0-y1)-x0(x1y0-x0y1)

a2(y0-y2)-x0(x2y0-x0y2)

a2(y0-y1)(my0-nx0)-a2(y0-n)(x1y0-x0y1)

a2(y0-y2)(my0-nx0)-a2(y0-n)(x2y0-x0y2)

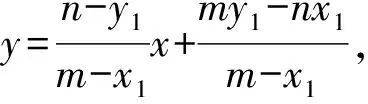
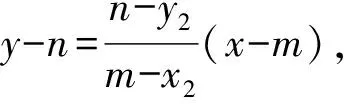
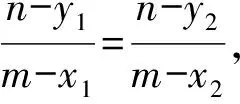
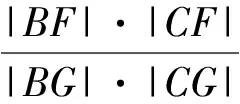
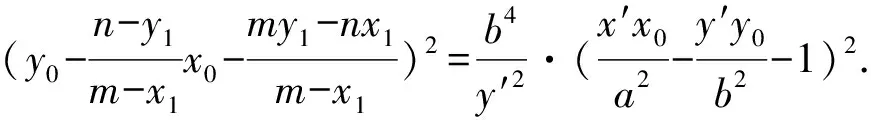
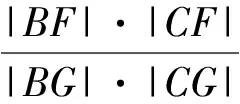
因为双曲线上的点(x0,y0)满足

联立直线DE的方程和双曲线方程

消去y,得

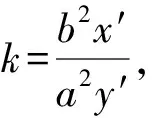
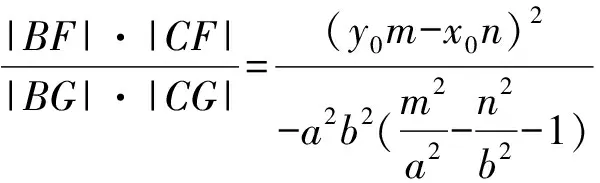
2 对与抛物线切线有关的一个定值的证明

引理4 过点A(x′,y′)作抛物线y2=2px的切线l1,l2,切点为D(x1,y1),E(x2,y2),则有

[yy1-p(x+x1)][yy2-p(x+x2)]

=[yy′-p(x+x′)]2-(y′2-2px′)(y2-2px).

抛物线上的点(x0,y0)满足

[y0y1-p(x0+x1)][y0y2-p(x0+x2)]

=[y0y′-p(x0+x′)]2.

证明因为切线l1,l2的方程分别为

y1y=p(x+x1),y2y=p(x+x2)，

根据引理2，过点A(x′,y′)的切线方程为

[y′y-p(x+x′)]2=(y′2-2px′)(y2-2px).

设[y′y-p(x+x′)]2-(y′2-2px′)(y2-2px)=μ[y1y-p(x+x1)][y2y-p(x+x2)]，其中μ为常数，等式两端的x项系数相等，得

2py′2-2p2x′=p2(x1+x2)μ.

联立直线DE的方程和抛物线的方程，

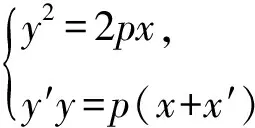
p2x2-(2py′2-2p2x′)x+p2x′2=0.

所以μ=1.

所以结论成立.

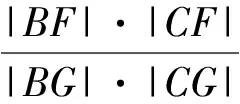
图2

证明记过点A的两条切线分别与抛物线相切于D，E两点，设A(x′,y′),D(x1,y1),E(x2,y2),F(x0,y0),因为点A在直线l上，所以点A的极线DE必过直线l的极点，坐标记为(m，n).

所以l的方程为ny=p(x+m),

AB的方程为y1y=p(x+x1),

AC的方程为y2y=p(x+x2),

BC的方程为y0y=p(x+x0).

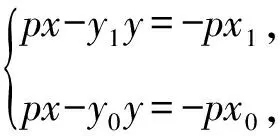
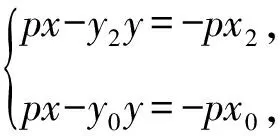
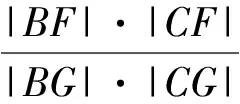
因为x0y1-x1y0-x0(y0-y1)

x0y2-x2y0-x0(y0-y2)

(y0-n)(x0y1-x1y0)-(y0-y1)(nx0-my0)

(y0-n)(x0y2-x2y0)-(y0-y2)(nx0-my0)

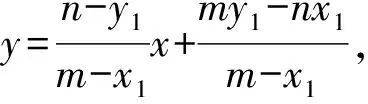
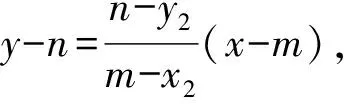
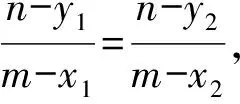
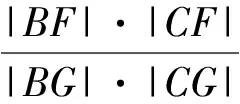
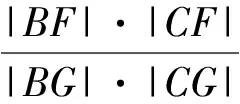
联立直线DE的方程和抛物线方程

k2(x-m)2+2(kn-p)(x-m)+n2-2pm=0.

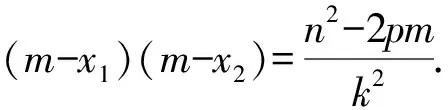
由DE方程为y′y=p(x+x′),

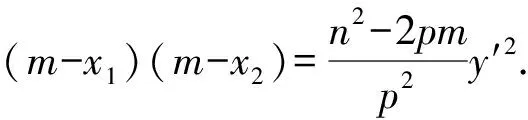
3 对与椭圆切线有关的一个定值的证明

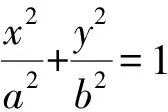
椭圆上的点(x0,y0)满足

引理5和定理3的证明见文[3].