例析高中数学与“圆”有关的最值问题

傅树兵

(福建省漳州招商局经济技术开发区海滨学校 363122)

与“圆”有关的最值问题解题思路灵活多变，其中函数视角、图形视角、对称视角、坐标视角、向量视角是解题的常用视角.不同视角适合分析的问题类型不同，解题细节存在较大差别，为使学生掌握不同解题视角的关键，教师应以经典例题为载体展开教学活动.

1 基于函数视角解题

基于对函数单调性的认识与理解不难发现，运用函数单调性解题时关键需把握两点：(1)构建正确的函数类型；(2)以函数为依托探讨最值问题需围绕自变量开展.能否正确地确定自变量范围，关系着求解结果的正确性，需根据习题情境以及实际情况，因此，应认真确定自变量的上限与下限.

例1 已知圆M和N的方程分别为：(x-cosθ)2+(y-sinθ)2=1(0≤θ<2π)，x2+y2-2x-4y=0.若两圆交于A，B两点，则tan∠ANB的最大值为____.

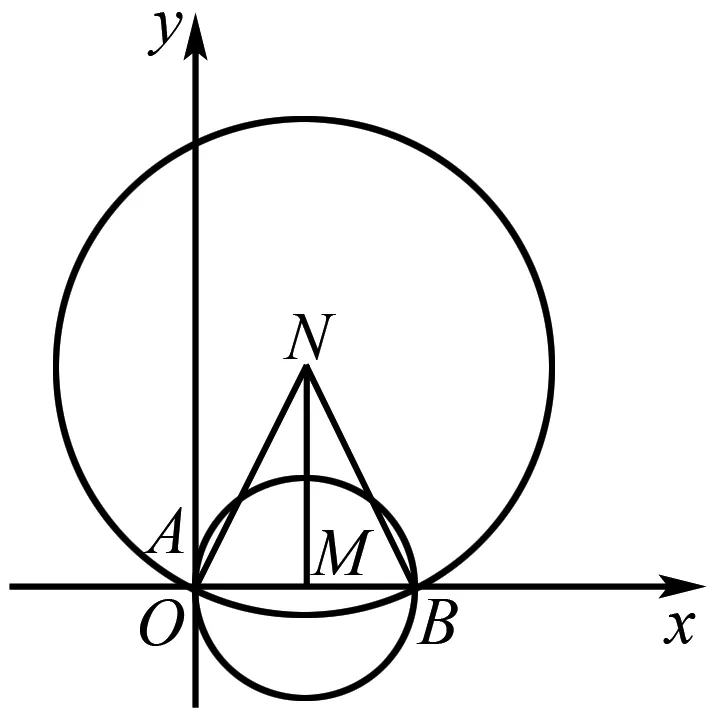
图1

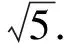
2 基于图形视角解题

例2 已知直线x+y=4上存在一动点P.过点P向圆O：x2+y2=4引两条切线，切点分别为A，B.在圆G：(x-4)2+(y-5)2=1上存在一动点M，则M到直线AB距离的最大值为____.

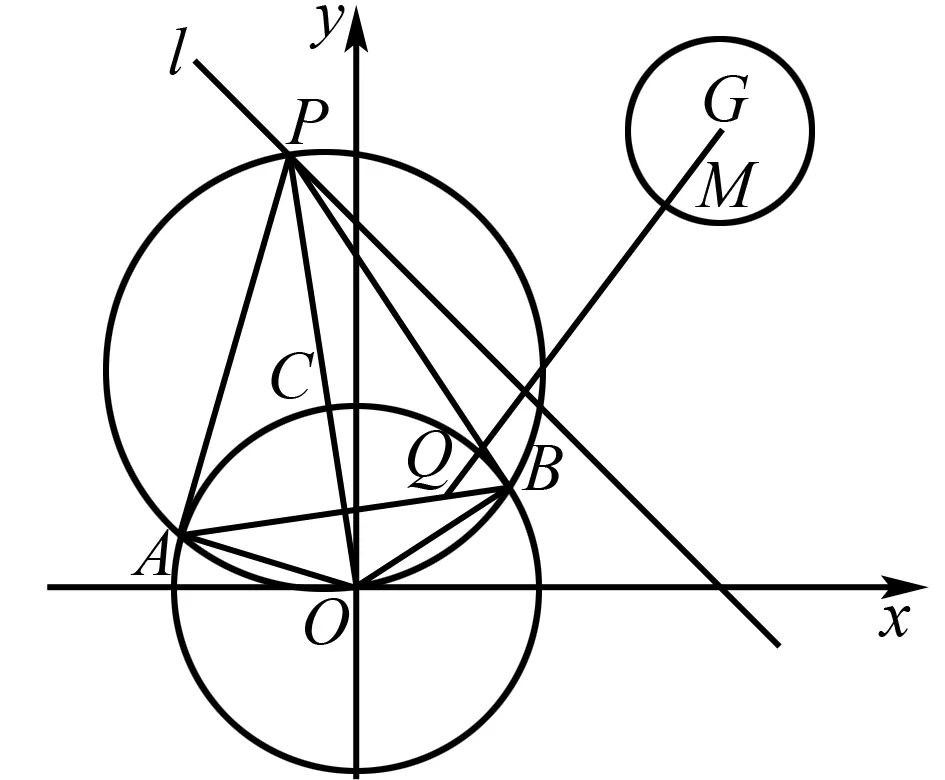
图2

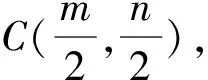
3 基于对称视角解题

基于对称视角解答与“圆”有关的最值问题，首先应突破如何寻找对称关系这一重点.寻找对称关系基于相关经验以及对图形关系的深入洞察，尤其需思考找到“对称”对象后接下来该怎么处理，是否实现了化难为易的目的.根据经验，经过“对称”处理后，最值点往往出现在点的共线上，并且这一共线关系和一些圆的圆心关系密切.在这一方向指引下不难寻找到正确思路，接下来只需认真计算即可.

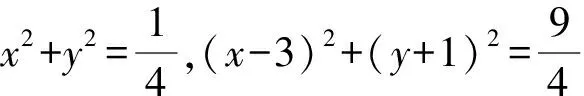
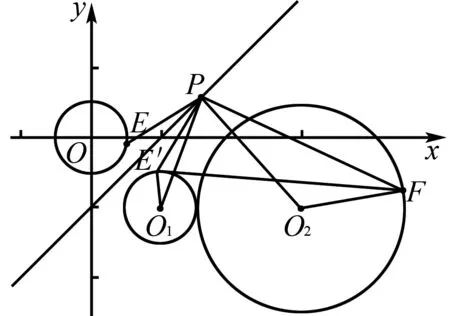
图3

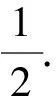
4 基于坐标视角解题

对于与“圆”有关最值问题的求解，可根据实际情况从坐标视角进行分析，通过坐标计算与图形关系的结合不难寻找到解题思路.众所周知，平面图形中点的坐标与平面直角坐标系位置密切相关.为降低计算复杂度应首先依托现有的图形、线段关系构建平面直角坐标系.在此基础上合理设出相关参数，对相关点的位置加以准确刻画.根据经验一些点的位置往往是动态变化的，其轨迹会形成一个圆或圆的一段弧.对于圆弧而言可借助圆的方程以及对应参数范围加以限定.以此为基础充分利用题干中的已知条件逐渐向要求解的问题靠拢，直到经过运算能够运用熟悉的知识顺利得出结果.

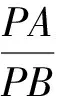
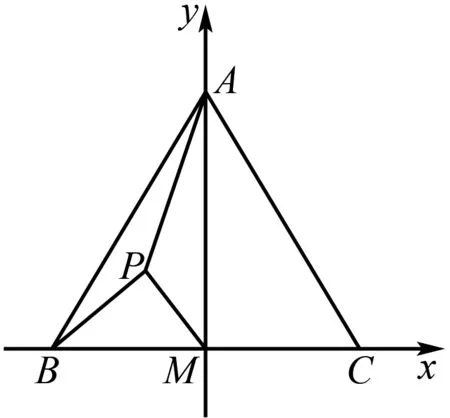
图4

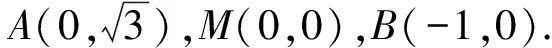
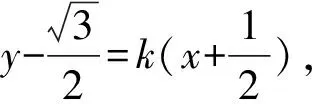
新课改思想对于教育教学有重要的指导作用，其要求的尊重学生学习成长阶段，循序渐进的指导学生学习的观点对于学生阅读能力的培养也有指导作用。在探索数学阅读之道的过程中，不能忽视新课改思想的应用，也不能忽视学生的身心发展阶段性，要循序渐进的指导学生阅读行为，培养学生阅读习惯。

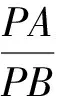
5 基于向量视角解题

向量与线段的区别在于向量具有方向性，使得其运算必须遵循自身的法则，但是向量的模与线段的长度是统一的.针对这一情况，可从向量视角解决一些与“圆”有关的最值问题.一般情况下，基于向量视角解决与“圆”有关的最值问题时，一般题干中都会有提示，如以向量的形式给出已知条件或者要求与向量相关的最值等.当然仅仅知道这一点是不行的，需充分运用已知条件通过抽象、运算、整理等处理，使得一些隐含的关系清晰地展示出来，为向量知识的运用做好铺垫.

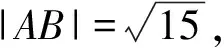
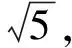
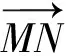
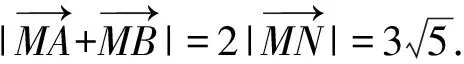
综上所述，高中数学与“圆”有关的最值问题是非常重要的一类问题.该类问题又被进一步细分为多种情境，而且不同情境应用的解题思路有时存在较大差别.实践中为使学生能够举一反三，实现解题能力以及解题灵活性的提升，在做好相关情境类似问题的基础上讲解常用的解题视角，并依托习题做好各视角在解题中的应用展示，鼓励学生多思考、多揣摩，将相关细节理解到位，把控到位.