2020年复旦大学强基计划第18题的多视角解答与探源
李 勇
(贵州省贵阳市息烽县第一中学 551100)
1 真题呈现
题目在△ABC中,AB=9,BC=6,CA=7,则BC边上中线长度为____.
此题乍看十分普通,细细品味后却发现内涵丰富,给人启迪.深刻而不深奥的一道试题既考查了学生数学建模能力,又考查了直观想象、数学运算等能力.
2 解法探究
如图1,取BC边的中点为D,连接AD,即求AD的长.
图1
视角1 借助公共角B(或角C).
解析不妨借助公共角B.
在△ABC中,由余弦定理有
AC2=AB2+BC2-2AB·BC·cosB.
所以49=81+36-2×9×6×cosB.
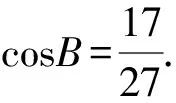
在△ADB中,由余弦定理有
AD2=AB2+BD2-2AB·BD·cosB
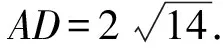
视角2借助∠ADB+∠ADC=180°.
解析在△ADB中,由余弦定理有
AB2=BD2+AD2-2BD·AD·cos∠ADB.
即AD2-6AD·cos∠ADB-72=0.
①
在△ADC中,由余弦定理有
AC2=CD2+AD2-2CD·AD·cos∠ADC.
所以AD2-6AD·cos∠ADC-40=0.
因为∠ADB+∠ADC=180°,
故cos∠ADC=cos(180°-∠ADB)=-cos∠ADB.
所以AD2+6AD·cos∠ADB-40=0.
②
由①+②,得2AD2=112.
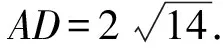
视角3 借助三角形的射影定理.
解析在△ADB中,由余弦定理,得
在△ADC中,由余弦定理,得
在△ABC中,由射影定理,得
a=ccosB+bcosC.
所以6=9cosB+7cosC.
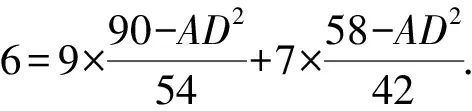
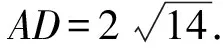
视角4 借助S△ADB=S△ADC.
解析设AD=x,
因为D为BC的中点,所以S△ADB=S△ADC.
由海伦公式,得
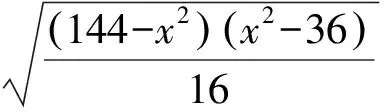
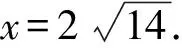
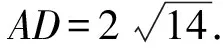
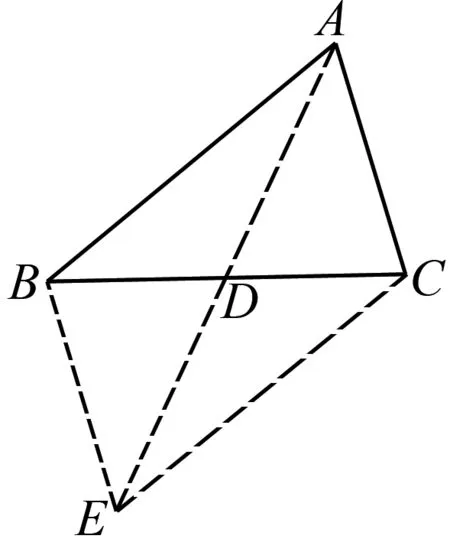
视角5 构造三角形的中位线,借助余弦定理.
解析如图2,过点D作DE∥AB交AC于点E.
在△ABC中,由余弦定理有
BC2=AB2+AC2-2AB·AC·cos∠BAC.
所以36=81+49-2×9×7·cos∠BAC.
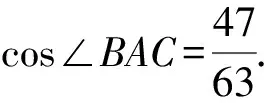
图2
由DE∥AB,所以∠BAC+∠AED=180°.
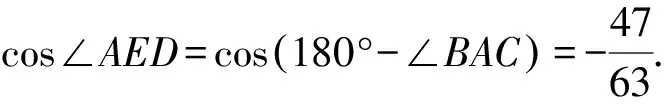
由DE∥AB,且D为BC的中点,AB=9,AC=7,
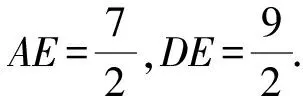
所以AD2=AE2+DE2-2AE·DE·cos∠AED
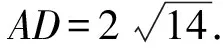
视角6 构造直角三角形,借助勾股定理.
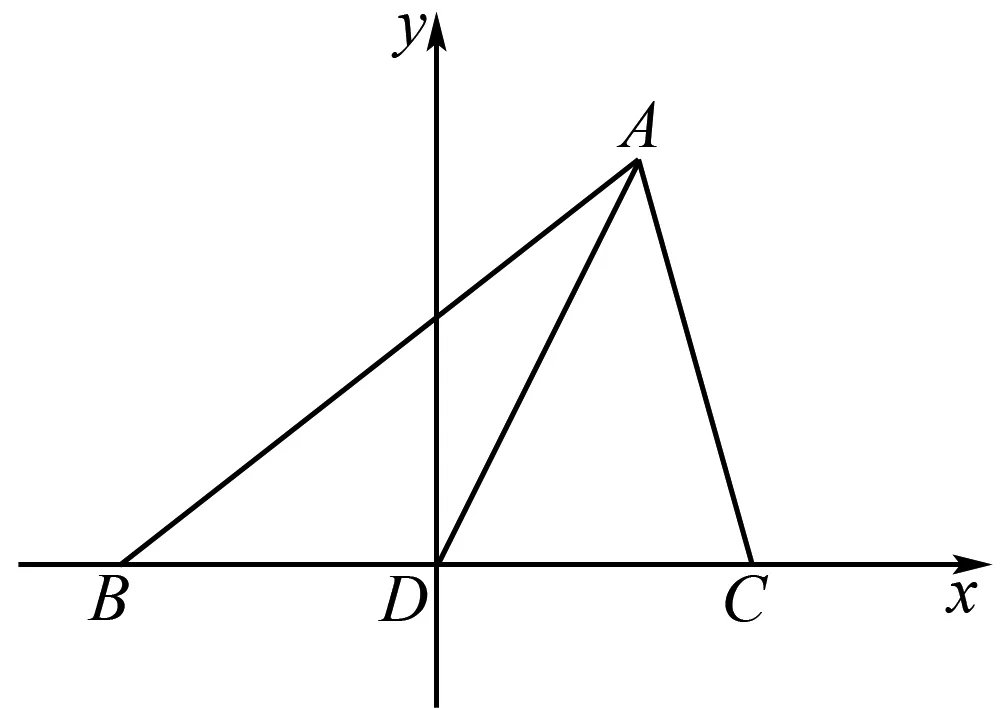
解析因为AB2 如图3,过点A作AE⊥BC,交线段BC于点E. 图3 设CE=x,则由勾股定理可得 AC2-EC2=AB2-BE2. 即72-x2=92-(6-x)2. 又由勾股定理可得 AD2-DE2=AC2-CE2. 解析在△ABC中,由余弦定理,得 因为AD是BC边上的中线, 视角8 借助平行四边形的性质:平行四边形的两条对角线的平方和等于平行四边形的两邻边的平方和的2倍. 解析如图4,延长AD于点E,使AD=DE,连接BE,CE,易知四边形ABEC是平行四边形. 图4 由平行四边形的性质,得 BC2+AE2=2(AB2+AC2). 所以62+AE2=2(92+72). 视角9 建立适当的平面直角坐标系,借助两点间的距离公式. 解析如图5,建立平面直角坐标系. 图5 则B(-3,0),C(3,0),D(0,0). 设A(x,y), 则AB2=(x+3)2+y2=81, ③ AC2=(x-3)2+y2=49. ④ 由③+④,得x2+y2=56. 视角10 借助三角形的中线长公式. 解析由三角形的中线长公式,得 本题来源于人教A版教材必修第二册第53页第15题. △ABC的三边分别为a,b,c,边BC,CA,AB上的中线分别记为ma,mb,mc,利用余弦定理证明 从表达形式可以看出,这道强基计划试题是教材中的试题进行数据改编而得的.近几年的自主招生,强基计划,各种竞赛试题的命制越来越新颖多变、形式多样,但万变不离其宗,它们都可以在教材中找到原型.因此,需要我们在平时的学习过程中留意对课本例题、习题、练习题的训练,要熟练地进行求解,掌握问题求解的通性通法,同时进行一题多解和多变练习,抓住实质,做到“胸中有本”,以不变应万变,一题一世界,一题可破万题山. 变式1 (2017年北京大学自主招生第6题)若三角形三条中线长度分别为9,12,15,则该三角形面积为( ). A.64 B.72 C.90 D.前3个答案都不对 解析如图6,设△ABC的三边分别为AB=c,BC=a,CA=b,三条中线分别为AD=9,BE=12,CF=15. 图6 由三角形的中线长公式,得 解析记M为AC的中点,由中线长公式,得 4BM2+AC2=2(AB2+BC2). 由余弦定理,得 解析设点B在面ACM上的射影为点O,则 由余弦定理,可得 因而∠OMC=150°. 对二面角B-MC-A的大小分类讨论. ①若二面角B-MC-A的大小为锐角, 则∠AMO=∠OMC-∠AMC=90°. ②若二面角B-MC-A的大小为钝角, 则∠AMO=360°-∠OMC-∠AMC=150°. 由余弦定理,可得 AO2=MA2+MO2-2MA·MO·cos150° 故选B,C. 变式4 (2021年复旦大学自主招生第3题)AD是△ABC的角平分线,AB=3,AC=8,BC=7,求AD的长. 解析1由三角形内角平分线定理得 所以3DC=8BD. 解析2 由角平分线长公式,得 教材是专家们花费大量心血进行千锤百炼、字斟句酌编写而成的,教材具有示范性和权威性,纵观近几年的自主招生、强基计划试题,可以发现许多试题都能找到课本习题、练习、例题的影子,试题中不变的是知识和思想方法,变化的无非是呈现的方式、问题的结构方式.这就要求我们平时在教学中,要对教材中经典的题目、具有代表性的题目特别关注,关注其解法,关注其变式,使学生知一题而懂一类.在提炼这些问题的基本方法、常规方法的同时,还要掌握不同题型的“秒杀法”,不论试题构思如何新颖,学生都能自如应对.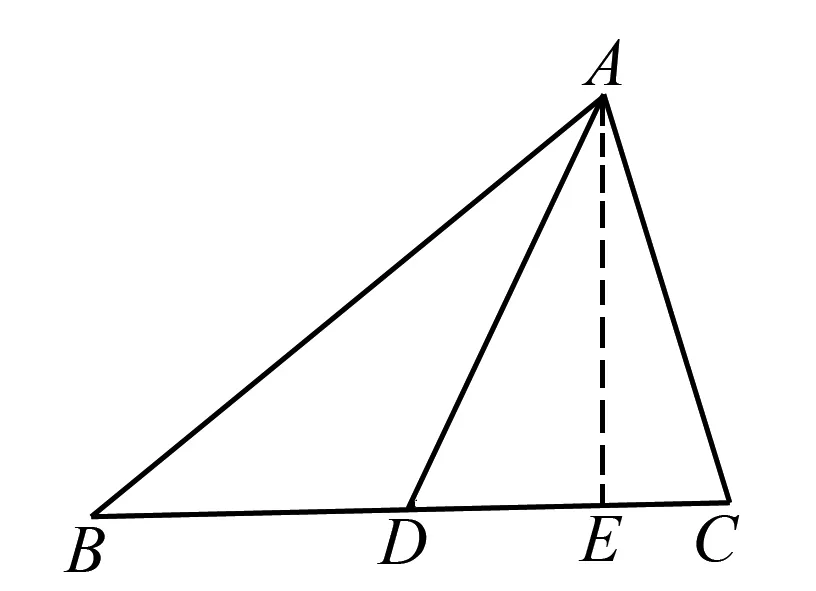
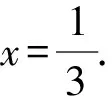
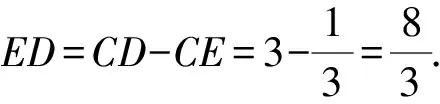
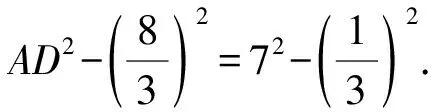
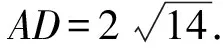
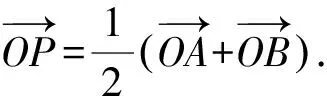
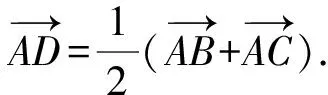
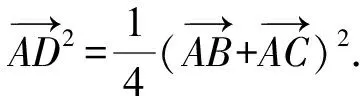
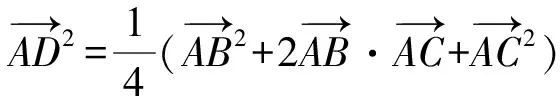
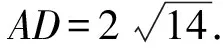
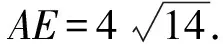
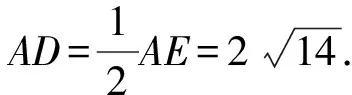
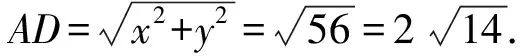
3 寻根探究
4 同源变式
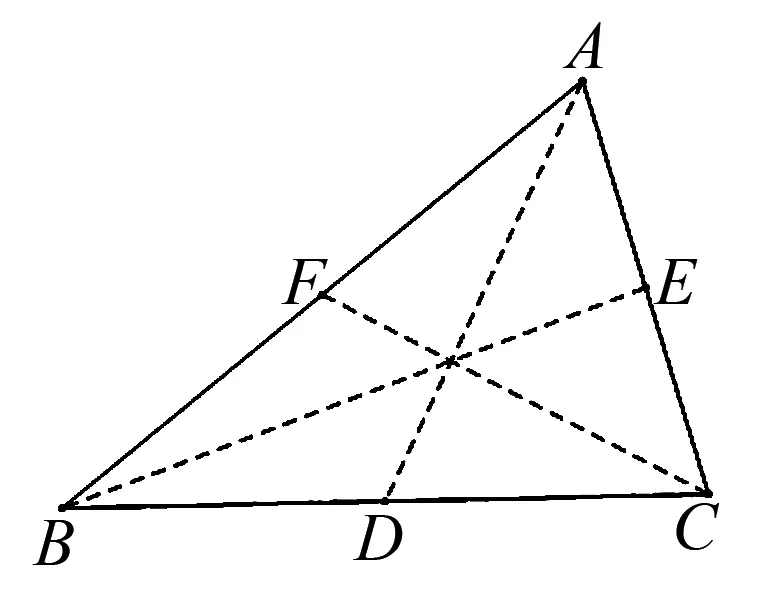
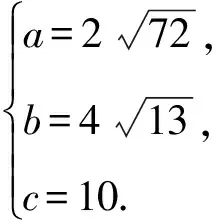
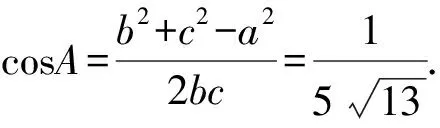
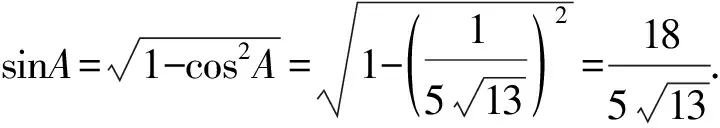
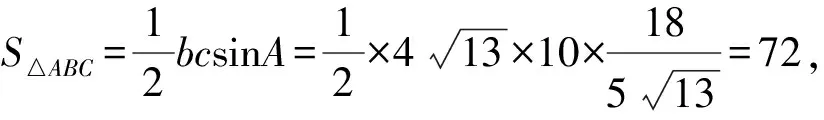
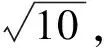
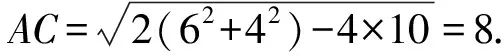
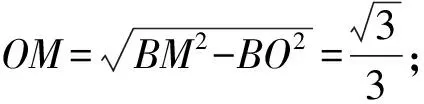
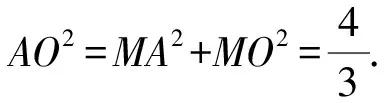
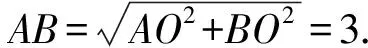
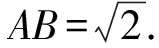

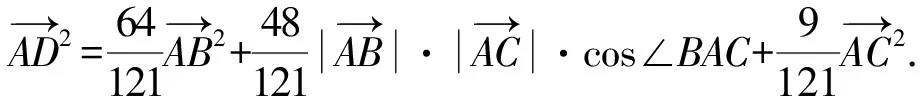
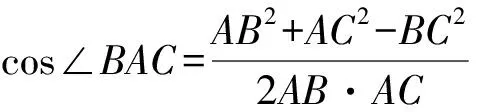
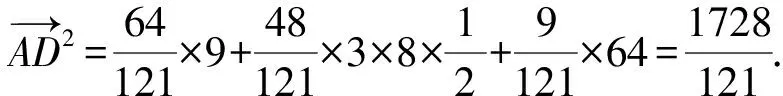
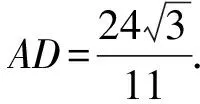
5 解题启示
——书写要点(三)

