研究题设条件 拓展应用价值——以江苏2008年高考物理第14题为例

张 萍

(江苏省清江中学 223001)

在高三复习备考过程中，为了把握高考命题的方向和命题思路，从专职教研员到学校一线教师，都特别注重对高考试题的分析研究.在市、县、校每一届高三复习第一次研讨会上，高考试题的分析研究通常都是研讨内容的重头戏.在高三复习教学过程中，教师经常会选择高考试题作为例题或习题，让学生亲历高考试题的分析解答过程，体悟高考试题究竟“考什么？怎么考？”探讨和总结解题的方法和策略，提升学生分析解决问题的能力和素养.为了充分发挥高考试题的应用价值，不能仅停留在符合参考答案正确解题的层面上，还可以根据试题及学生的具体情况，对高考试题进行适度变化和拓展，以期达到举一反三、事半功倍的教学效果.下面以2008年江苏高考第14题为例，展示高考试题拓展应用的新视角.

2008年江苏高考第14题：在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O点静止释放，小球的运动曲线如图1所示．已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g．求：

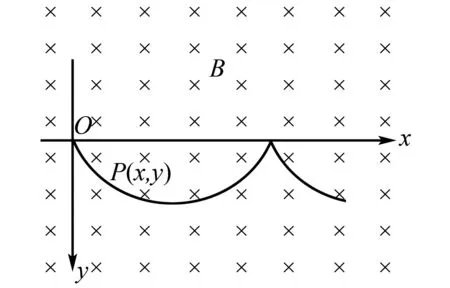
图1

(1)小球运动到任意位置P(x，y)的速率v.

(2)小球在运动过程中第一次下降的最大距离y.

解答见参考文献[1]，此处略.

评析本题是一道中等难度的电磁学综合题.考查内容涉及洛伦兹力、电场力、向心加速度、向心力等常用知识点，以及动能定理、牛顿运动定律等重要规律.突出了对考生运动观、能量观等物理观念的考查，突出了对考生分析推理等物理思维能力的考查.考生在解答该题时，必须要对小球进行受力分析、运动分析和能量分析，受力分析时要注意小球重力不可以忽略，运动分析时要认识到小球的运动是复杂的曲线运动，不是圆周运动.能量分析时要认识到小球重力势能、动能和电场能的相互转化.因为重力、电场力是恒力，洛仑兹力虽是变力但却始终不做功，所以用动能定理恰当，根据题设条件，牛顿第二定律只能运用到最低点这个状态.

拓展教学实践中，解答该题后，根据学生实际情况，特别是对部分优生，可以追问题目中给的条件：为什么此曲线在最低点的曲率半径为该点到x轴距离的2倍？能证明吗？

以下简要给出三种不同证明方法.

设小球到最低点时速度为v，最低点到x轴距离为y，曲线在最低点的曲率半径为R

方法一判别式法

在最低点，由牛顿第二定律得

整理得mv2-qBRv+mgR=0

上式是关于v的一元二次方程，因为在题设条件下v是客观确定的，故方程不可能有两解，只能有唯一解.由数学知识可知，对于一般的一元二次方程ax2+bx+c=0，有唯一解的条件是判别式应为0，即b2-4ac=0，应用到本题得(qBR)2-4m×mgR=0

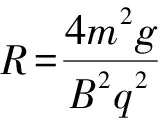
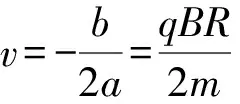
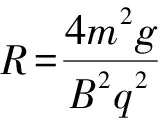
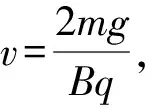
比较R与y表达式，显然R=2y

方法二微元法

到最低点过程中，水平方向运用动量定理得

∑qvyBΔt=mv而∑vyΔt=y

可得qBy=mv

所以R=2y

方法三运动分解法

下降的最大距离y等于匀速圆周运动这个分运动圆周的直径，即y=2r

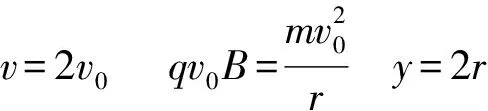
三个关系式消去v0和r得qBy=mv

所以R=2y

以上拓展的问题切合学生特别是优生的实际，没有盲目为变而变，解答该拓展问题涉及到高中物理多个重要规律，特别是解决问题的思路方法典型又多维，有利于培养学生思维的深刻性、广阔性和批判性，因此这样的拓展很有意义.