核心素养背景下高中数学导数问题求解策略分析
任丹
【摘要】数学核心素养作为高中数学教学的指挥棒、方向标,不仅能促进数学教学改革,赋能数学课堂教学,还能培养学生的逻辑推理、直观想象及数学模型建构等学科技能,从而带动学生综合解题能力的发展.而导数问题作为近年来高考考查的热点,在其解题教学中渗透核心素养,有利于进一步提升学生的导数问题求解能力.为发挥核心素养对学生导数问题求解的促进提升作用,文章将基于核心素养深入探究数学导数问题求解的有效策略.
【关键词】核心素养;高中数学;导数问题;求解策略
函数单调性、最值、不等式取值范围等问题均是导数知识点考查的重点,解决这些导数问题不仅要求学生熟悉导数的基本知识概念,能灵活迁移转化知识,还需要学生具备数形结合、分类讨论等思想能力,对学生的逻辑推理能力、直观想象能力也提出了较高的要求.随着学科育人思想理念的更新迭代,学科核心素养的培养已成为衡量课堂育人实效性的标准之一,并深受广大教育工作者的认可.对此,笔者将基于对核心素养的认识,简述对导数问题求解策略的见解.
一、在核心素养下研究高中数学导数问题解题策略的意义
(一)有助于强化学生导数问题求解能力
在核心素养指引下对高中数学导数问题求解策略进行研究,既能促使相关教育工作者重新审视导数解题教学,关注学生学科素养的发展情况,还能促进导数解题教学架构的合理规划,全面提升学生导数问题求解能力,帮助学生建构完整的导数知识模型.而学生亦能借此科学提升导数解题能力,发挥学科核心素养对导数问题求解的辅助效能,摆脱传统模板化解题的状态.
(二)有助于培养学生的学科素养
导数问题求解是学生发现、研究、创造数学的一个动态过程,在此过程中,学生能充分体会数学知识由已知转化为未知、由抽象到具体、由定量到定性、由理论到实际的方法技巧,掌握问题发现、切入、探究及处理的具体手段,锻炼并强化导数应用能力,以更好地理解导数的性质、内涵以及应用等,继而潜移默化地对学生的直观想象、逻辑推理及数据分析素养产生积极的导向促进作用,带动学生数学核心素养的发展.此外,导数问题作为集抽象、逻辑、数据于一体的综合性问题,与数学核心素养有着异曲同工之妙,故学生在导数问题求解训练中,也在不断地强化个人的学科素养.
二、核心素养下高中数学导数问题求解策略
(一)逻辑推理转化问题,用导数求解不等式问题
不等式恒成立问题与不等式证明问题作为导数问题的重要组成,是高考导数知识考查的热点.不等式恒成立问题可通过逻辑推理转化为函数的最值问题,再套用导数处理函数最值问题的方式进行解题.而对于不等式证明问题,可利用邏辑推理转化为函数的单调性问题.对此,教师不妨在利用导数处理不等式问题教学中侧重发展学生的逻辑推理能力,在解题环节引导学生关注不等式问题转化的条件,将未知信息转化为已掌握的函数知识,推理演绎出解题的思路,降低不等式问题求解的难度.用导数逻辑推理转化不等式问题的解题策略如下.
例1 已知函数f(x)=sinx(x≥0),g(x)=ax(x≥0),若f(x)≤g(x)恒成立,试求实数a的取值范围.
解析 根据题意,f(x)≤g(x)恒成立,代入原函数式可得到一个不等式,再根据所求的是实数a的取值范围,便可推理出本问题主要是用导数处理不等式恒成立问题.

反思:学生在用导数处理函数问题时,可先进行简单的函数式代入化简,若得到如例1中的f(x)≤g(x)恒成立不等式,便可根据上述导数求解不等式问题的思考切入方式,将其转化为函数最值与0的关系,从而进行求解.同时,将f(x)≤g(x)恒成立问题转化为f(x)与g(x)的图像关系,且前者图像应恒在后者图像下方.以上解题策略的探讨可带动学生逻辑推理能力的发展,达到发展学生学科核心素养的目的.
(二)数形结合直观想象,用导数求解最值问题
用导数解函数最值问题,一般需要学生先结合函数单调性求出函数的零点,再通过数形结合思想将其转化为具体的函数图像,根据图像的变化情况逆向思考是否符合题意,再直观想象推演出函数极值点.值得注意的是,该类型问题求解的关键是作图,教师需要在解题教学中侧重引导学生利用数形结合处理最值问题,引导学生养成作简图的习惯,以辅助学生更好地进行直观想象,高效求出导数问题的最值,达到发展学生直观想象素养的目的.
例2 已知A地为海中小岛,距离公路BC的直线距离AB=50km,且公路一端的B地与另一端的C地相距100km.若小明打算从海岛A地到C地,先借助速度为25km/h的小船到达公路BC上的D处(不与B,C重合),再乘坐速度为50km/h的小汽车从登陆点D去到C地,试分析登陆点D应当设在何处才能使小明所使用的时间最短.
解析 本例题主要考查学生函数关系建立及用导数求解函数最值问题.由于条件较为抽象,学生可通过数形结合辅助求解,从而更快地建立函数式进行最值求解.

反思:利用数形结合思想求解导数问题能为学生思考提供方向,使得学生更加迅速地找到问题切入点,化抽象要素为具体要素,将未知问题转化为导数求最值问题.
(三)分类讨论数据分析,用导数求解函数单调性
导数单调性问题是近年来高考热点,其大多与一元二次不等式相结合,需要学生根据导数与函数单调性所存在的关系判断函数的单调性.该类型问题的本质就是讨论分析导函数f′(x)的值的正负问题.而分类讨论思想作为处理该类导数问题较为常用的思想,是学生处理该类型问题必须具备的思想能力.同时,分类讨论思想能帮助学生强化数据分析能力,培养学生在不同情境中收集、分析、处理信息思维素养,使学生能结合题目条件灵活讨论、求解函数的单调性,帮助学生高效处理导数单调性问题.
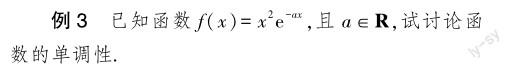
解析 根据题意,可知参数a会对函数图像产生影响,故a的取值决定着函数的单调性,所以本题主要应先求f(x)的导数,然后利用分类讨论思想对a进行分析,得出函数的单调性.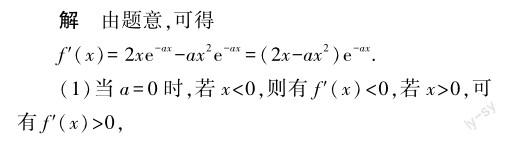

反思:本例题主要考查函数单调性判断问题,可直接归纳到f′(x)的符号判断上,而对于f′(x)>0或f′(x)<0问题,则可先将其转化为一元一次或一元二次不等式问题,再结合分类讨论思想进行讨论.
(四)建构模型导向实践,用导数求解实际问题
用导数求解实际问题,是学生提升知识迁移整合能力、综合解题能力的最佳手段,也是贯彻实践育人思想的重要体现.近年来,导数问题联系生活实际的题目渐多,同时,此类型题目需要学生综合运用最值、零点、单调性等函数知识,对学生的综合解题能力要求较高.对此,教师可通过整合以上多种解题策略,联系生活实际,帮助学生积累用导数处理生活问题的经验和技巧,逐步建构与之相匹配的导数解题模型,带动学生导数解题能力素养的发展,最终达到用生活实践数学模型建构带动学生导数解题能力的目的.

反思:本例题中涉及函数的众多知识,考查学生建构模型处理实际问题的能力,教师可通过用导数处理实际问题的数学模型来帮助学生解题:(1)列函数式y=f(x);(2)对y求导,并令y′=0;(3)求得x,解决实际问题.教师应通过数学模型建构提升学生的实际问题处理能力.
结 语
综上所述,导数问题求解教学可发展学生的核心素养,符合新高考考查学生知识技能的思想理念,故教师用核心素养创新指引高中数学导数问题求解策略势在必行.教师应基于核心素养推进导数问题求解教学体系架构,輔助学生建构完整的导数解题模型,发展学生的导数思维意识,锻炼学生的导数解题技能,以助力学生综合提升导数解题能力,最终达到发展学科核心素养的目的.
【参考文献】
[1]陈尔明,陈坤其.基于数学核心素养的试题命制与解析:以“导数解决零点问题”为例[J].高中数学教与学,2020(18):33-35.
[2]王洋洋.继承和构造思想在高中数学导数问题中的运用[J].数理化解题研究,2019(28):26-27.
[3]勇乐慧.分类讨论在高中数学导数问题中的应用[J].数理天地(高中版),2023(1):4-5.

