“双减”政策背景下小学数学作业分层设计实践研究
谭文昌
【摘要】“双减”政策下,传统的作业模式面临着极大的挑战.鉴于此,为了充分发挥作业的价值和功效,教师必须彻底摒除传统的作业设计模式,以分层作业设计理念为指导,为不同层次学生量身打造一套具有针对性的作业内容,以提升作业的有效性,促进学生的全面发展.文章就聚焦于此,简述了“双减”政策下分层作业设计的内涵和基本原则,并结合数学教学案例,针对分层作业设计路径展开了详细的探究,旨在落实“双减”政策的要求,提升小学数学作业设计质量.
【关键词】“双减”;小学数学;作业设计;分层作业
【基金项目】本文系2022年贵州省教育科学规划民族地区基础学科(领域)质量提升专项课题《双减政策背景下小学数学作业分层设计实践研究》(课题立项号:MJ22087)的研究成果之一.
在整个教育体系中,小学是夯实学生基础知识的关键时期.课后作业作为中小学教育体系中的重要组成,承担着巩固知识、发展思维、提高能力、培养习惯等多重任务,是提升学生学习效果的关键.目前,受传统作业设计理念的制约,部分教师依然倾向于“题海战术”,使设计出来的作业存在任务重、缺乏连贯性和持续性、内容不科学等问题,这不仅为学生带来了极大的课后压力,也限制了学生的思维发展.而“双减”政策倡导教师从素质教育和核心素养的角度出发,尊重学生的差异性,为其量身打造一套适切性的作业练习.
一、“双减”政策下分层作业设计的内涵和基本原则
(一)分层作业设计的内涵
“双减”政策下,分层作业设计模式逐渐走进教师的视野.与“一刀切”作业设计模式不同,分层作业设计立足于学生的个体差异,尊重学生的学习需求,使得学生在针对性的作业中获得成就感、自信心.具体来说,分层作业设计以学生的个体差异性为出发点,结合学生在学习成绩、知识范围、智力发展水平、知觉敏感力、学習兴趣和学习态度等方面存在的差异性,设计出差异化的数学作业.具体来说,分层作业设计集中体现在两个方面:一方面,对学生进行分层.教师应对学生的知识掌握情况、学习态度、学习兴趣、思维能力等进行全面的分析,基于学生之间的差异性,对学生进行科学、合理的分层,确保设计出来的数学作业能够兼顾不同层次学生的学习需求.另一方面,对作业的程度进行分层.在分层作业设计理念下,教师应根据教学目标和教学内容将作业划分为不同的等级,并从作业量、作业难易程度、作业形式等方面进行优化设置,旨在满足不同层次学生的学习需求.
(二)分层作业设计基本原则
鉴于“双减”政策下作业设计的必要性和要求,教师应遵循以下四个原则优化分层作业设计.
原则一:科学性.一方面,“双减”政策下,教师在设计分层作业时必须以新课程标准为依据,内容也必须合理,紧扣教材内容,不能与现行的课程标准、教学内容相背离;另一方面,在分层作业设计中,教师应考虑学生的知识水平和结构的差异性,作业难度应适用于各个层次学生的需求,使得每一个层次学生都能在作业中感悟到数学学科的魅力,并从中获得成长和发展.
原则二:发展性.“双减”政策下,分层作业设计旨在促进所有学生的发展.教师在设计分层作业时,必须以科学发展观为指导思想,确保设计出来的分层作业能够促进学生的个性化、可持续发展.同时,教师在设计作业时应兼顾作业的“质”和“量”,避免简单重复性的作业.
原则三:启发性.“双减”政策下,教师在设计分层作业时还应关注作业的启发性,确保设计出来的作业能够唤醒学生的探究兴趣,并使得学生在探索解题思路的过程中促进知识的内化、能力的提升和数学思维的发展,真正实现学生的全面发展.具体来说,“双减”政策下,教师应遵循启发性的原则,采用多种方式设计分层作业,使得学生在多样化的层次性作业探究中获得综合性发展,并形成浓厚而持久的学习动机.
原则四:层次性.“双减”政策下,教师在设计课后作业时必须基于学生的认知发展区,坚持因人而异的原则科学设计课后作业.这就要求教师在设计作业之前对小学生的学习特点、学习能力、知识掌握情况、学习态度等进行全面的了解,并基于学生的实际情况将作业划分为基础性、提高性和拓展性作业,以满足不同层次学生的实际需求.
二、“双减”政策下小学数学作业分层设计策略
(一)以生为本,关注学生的作业需求
“双减”政策契合了新课标的要求,倡导教师在组织课堂教学、设计课堂作业时坚持以生为本的理念,以学生的认知发展水平为基础,以促进学生的全面发展为主要目标.鉴于此,教师在设计分层作业时应提前做好学情分析,了解学生的数学基础知识、学习能力、思维发展水平、学习态度等,精准把握学生的实际情况.而要达到这一目标,教师在设计作业之前应充分利用课堂互动、课后交流、考试和作业诊断等方式了解班级内学生的学习情况,精准把握学生的数学学习潜能,在此基础上结合学生的知识水平、学习能力等将作业划分为基础层、提高层和拓展层三个层次.另外,教师应在此基础上,基于不同层次学生的学习需求制订不同的作业目标,确定不同的作业内容,使得学生在层次分明、结构合理的作业中获得不同程度的进步和发展.
例如,在人教版六年级下“比例的应用”这一节课的作业设计中,为了落实“双减”政策的要求,聚焦这一章节的重要知识点———比例尺,以及具体的教学目标,教师可结合基础层、提高层和拓展层三个层次学生的实际需求,为学生设计出以下层次化作业.
【基础题】
(1)一幅图中( )和( )的比叫作这幅图的比例尺.比例尺分为( )比例尺和( )比例尺.
(2)地图上2cm的线段表示实际距离6km,则地图的比例尺是( ).
(3)已知一个零件的实际长度为8mm,该零件在图纸上的长度为48cm,则制作该零件图纸时采用的比例尺是( ).
(4)填表.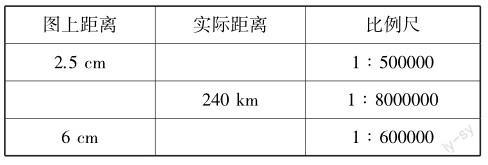
【提高题】
(1)一幅地图的比例尺为1∶2500000,经测量,天津到北京的距离为4.8cm,求两地之间的实际距离是多少千米.
(2)学校的会议室长为12m,宽为8m,请你用1∶400的比例尺将其平面图画出来.
【拓展题】
已知某一地图的比例尺为1∶2000000,A,B两地的图上距离为6cm.甲、乙两车同时从A,B两地出发,相向而行,2h后两车相遇.已知甲、乙两车的速度比为2∶3,则两车的速度分别是多少?
纵观基础题、提高题和拓展题,均聚焦本节课教学内容———比例尺,并聚焦本节课教学目标,同时凸显了生本理念,基于班级内基础层、提高层和拓展层的学生设计出针对性的作业练习.其中,基础题目是对基础知识的巩固和应用,旨在引领学生真正理解比例尺的含义,以及运用比例尺的概念进行求解;提高题的难度随之提升,基于实际生活中常见的问题,对学生的问题分析能力、知识应用能力、动手操作能力进行了考查,满足了班级中提高层学生的需求;拓展题的难度进一步提升,将比例尺和相遇问题整合到一起,为学生提供了挑战的空间,使得学生在探究中促进了数学思维、综合能力的发展,满足了拓展层学生的学习需求.
(二)设计弹性作业,促进学生动态发展
“双减”政策下,教师在设计课后作业时还应立足于“最近发展区”理念,基于不同层次学生的学习需求,为其设计出富有弹性的数学作业.这主要是因为学生的学习能力、认知发展水平并非一成不变的,而是呈现动态发展的状态.但是学生的这种变化并不明显,而是在潜移默化中逐渐提升的.因此,教师在落实“双减”政策时必须坚持因材施教的理念,基于学生的动态发展变化,为其设计契合学情的弹性数学作业.
例如,在人教版四年级上“公顷和平方千米”的课后作业设计中,教师在落实“双减”政策时应从学生当前的实际学情出发,为其设计弹性化的作业,以促进学生的动态化发展.据此,教师可将这一章节数学作业划分为必做题和选做题两大类.
【必做题】
(1)判断下列说法是否正确.
①6公顷=60000平方米.( )
②在日常生产实践活动中,常常用“平方千米”作为比较大的土地面积的计量单位.( )
(2)填上合适的单位.
华山的占地面积约为150( );学校占地面积约为1万( );鸟巢建筑物的占地面积约为20( ).
【选做题】
(1)学校打算修建一个运动馆,其长度为50m,宽度为25m,运动馆的占地面积为多少公顷?
(2)王叔叔家有一片果园,其长度为400m,宽度为200m,如果果园每公顷的水果产量为20吨,这个果园一共能够产出多少吨水果?
(3)学校组织体操表演,在面积为1公顷的正方形操场上,学生之间相隔2米站成方队,那么操场能够容纳多少学生?
在这一题作业中,必做题聚焦本节课教学内容和教学目标,并以判断和填空的形式出现,突出了作业的基础性以及数学知识和实际生活的内在联系,应面向基础层和提升层学生;选做题应面向成绩好、数学思维能力强的拓展层学生.基础层学生在学有余力的基础上可完成选做题的前两道题.针对提高层的学生来说,选做题中的前两道题目属于必做的范畴,在学有余力的同时可完成选做题的第三题.针对拓展层的学生来说,应完成所有作业.如此一来,在弹性化的数学作业中,学生可结合自己的实际情况自行选择作业内容,并在针对性的训练中感悟到数学知识的魅力,在快乐学习中获得数学综合素养的形成与发展.
(三)控制作业总量,丰富作业类型
“双减”政策下,小学数学教师在设计分层作业时必须基于“双减”政策的要求,从总体上控制作业的数量,并根据不同层次学生的需求精心安排针对性的作业.具体来说,针对基础层的学生,教师应尽量选择典型的题目,确保其覆盖所教内容的全部知识点,以便其在针对性的训练中增强学习自律性,产生强烈的学习动机;针对提高层学生,教师应将作业量控制在必做题和选做题之间,使其在完成必做题的基础上根据自己的时间和能力思考选做题;针对拓展层学生,教师则应遵循“少而精”的原则,适当减少作业量,增加作业的难度,使其在思考和探究中获得综合性发展.
例如,在人教版四年级下“运算律”的作业设计中,教师就可遵循上述原则,对作业量进行如下安排.
针对基础层学生,为其精选典型计算类题目.
(1)37×25×4,43×125×8.
(2)357+288+143,129+165+171+235.
(3)(80+4)×25,(125+17)×8.
針对提高层学生,设计“必做+选做”题目.
【必做题】
(1)学校组织五年级学生去游学,已知男生有184人,女生有216人,如果一辆大巴中能够乘坐40名学生,则学校一共要安排多少辆大巴?
(2)甲、乙两名工人合作加工一批零件.已知甲每分钟能够加工零件51个,乙每分钟能够加工零件49个,如果两人合作加工,6分钟即可完成.那么,这一批零件一共有多少个?
【选做题】甲、乙两辆货车,同时从A城、B城出发,两车相向而行.已知甲、乙两辆货车的速度分别为40km/h,50km/h,两车一共用了6h完成全程,则A,B两地的距离为多少?
针对拓展层学生,为其设计三道题目.
思考下列题目的简单计算方法:
32×95,28×225-2×225-225×6,
39×8+6×39-39×4.
如此一来,基础层、提高层和拓展层学生虽然面临的作业存在一定的差异性,但三个层次学生均在作业练习中掌握了运算定律这一章节中的重点内容,并从中获得了不同程度的进步和发展.
结 语
综上所述,“双减”政策下,基于小学生的实际需求设计层次化的数学作业已经成为教师要研究的重点.教师作为课后作业设计者,应突破传统“一刀切”“题海战术”的作业设计理念的束缚,立足于学生的认知发展区,坚持因人而异的原则,为不同层次学生量身打造一套针对性强的作业题目,使得学生在针对性作业中促进知识的巩固与发展、数学思维能力的提升与发展,真正落实数学核心素养下的教学目标.
【参考文献】
[1]孙金禄.“双减”背景下小学数学作业分层设计的策略研究[J].试题与研究,2023(22):51-53.
[2]黄婷.“双减”视角下的小学数学作业分层创新设计策略[J].亚太教育,2023(14):141-143.
[3]马晓梅.“双减”背景下小学数学作业分层设计的策略研究[J].天津教育,2023(19):85-86.

