利用Mathematica研究四电荷系统的电势与电场强度分布

曲 浩 冯 豪 郭芳侠

（陕西师范大学物理学与信息技术学院，陕西 西安 710119）

在高中电学学习中，由于电势以及电场强度的抽象性与复杂性，学生理解起来较为困难.受限于高中阶段物理知识以及数学工具的深度，学生往往只能利用对称性和叠加原理进行局部的定性分析，不能对复杂电场进行精确计算，从而全面分析和呈现电场和电势的特征.以往研究中，陈燕［1］和许冬保［2］分别对等量和不等量的两个点电荷激发的电场、电势进行了讨论，董顺成［3］利用Geo-Gebra软件呈现两个点电荷在不同电性、不同电荷量情况下的电场分布情况，而对于四电荷系统激发的电场的研究较少.

本文首先从理论上计算4个位置对称的点电荷在空间中产生的电场和电势，然后应用Mathematica软件直观展示静电场的分布，为教师教学和学生学习提供有力支持和帮助.

2022年高考全国乙卷物理试题第19题如下.

如图1，两对等量异号点电荷＋q、－q（q＞0）固定于正方形的4个顶点上，L、N是该正方形两条对角线与其内切圆的交点，O为内切圆的圆心，M为切点.则

图1

（A）L和N两点处的电场方向相互垂直.

（B）M点的电场方向平行于该点处的切线，方向向左.

（C）将一带正电的点电荷从M点移到O点，电场力做正功.

（D）将一带正电的点电荷从L点移到N点，电场力做功为零.

答案：（A）（B）.

本题情境是静止、等量的两个正电荷和两个负电荷构成的体系，主要考查学生运用点电荷电场、电势分布解决复杂电场中特殊场点的问题以及电场力做功的应用，对学生的学习迁移能力要求较高.图1中的L、N和M 3点的电场方向、电势很容易利用点电荷电场、电势规律及叠加原理解决，这里不再赘述.下面进一步分析4个电荷所在的正方形平面内各点的电场和电势分布，以期全面地展示电场和电势的分布特点.

1 电势与电场强度分布的计算

为方便对一般情形的分析讨论，将正方形顶点的4个点电荷设为q1、q2、q3、q4，并设正方形 的边长为2R，则内切圆的半径为R.以O点为原点，建立x Oy直角坐标系，如图2所示.

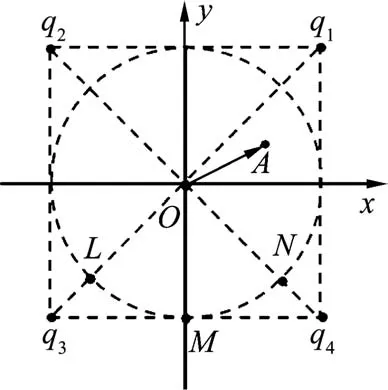
图2

则4个电荷的坐标为q1（R，R）、q2（－R，R）、q3（－R，－R）、q4（R，－R）.这里仅讨论x Oy平面内的电场分布，设平面内任意一点A的位矢为

r＝x i＋y j，取无穷远处为电势零点，4个点电荷在A点产生的总电势为

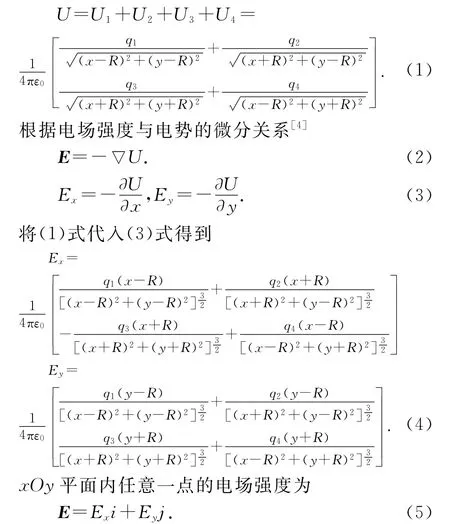
通过（1）（4）（5）3个表达式，就可以得到x Oy平面内任意点的电势和电场强度.

2 电势与电场分布图像

为使图2的点电荷系统在空间中产生的电场和电势更加直观，利用Mathematica进行计算并绘制图像.

2.1 x Oy平面内的电势分布

使用 Mathematica软件计算（1）式，并利用ContourPlot以及Plot3D命令绘制点电荷所在平面（xOy平面）内的等势线图和电势高低变化的立体图，分别如图3、图4所示.

图3形象直观地显示出4个点电荷所在的二维平面上电势的分布情况.由图可以看出，正电荷附近电势较高，负电荷附近电势较低；一、三象限电势为负，二、四象限电势为正；正方形的各边垂直平分线上（x轴和y轴）的各点电势都为零，是等势线；相邻电荷间等势线最为密集，反映了在该区域电场强度相对较大.图4则很好地反映了x Oy平面内电势大小的相对变化，正电荷周围图像凸起（电势为正），负电荷周围图像凹陷（电势为负），相邻电荷间电势梯度最为“陡峭”，反映出该区域电场强度是相对较大的.对称性方面，电势关于正方形的两条对角线对称.因此不难判断图1中将一带正电的点电荷从M点移到O点，两点位于同一等势线上，故电场力不做功；而将一带正电的点电荷从L点移到N点，两点电势不同，电场力一定做功.故而（C）（D）选项错误.

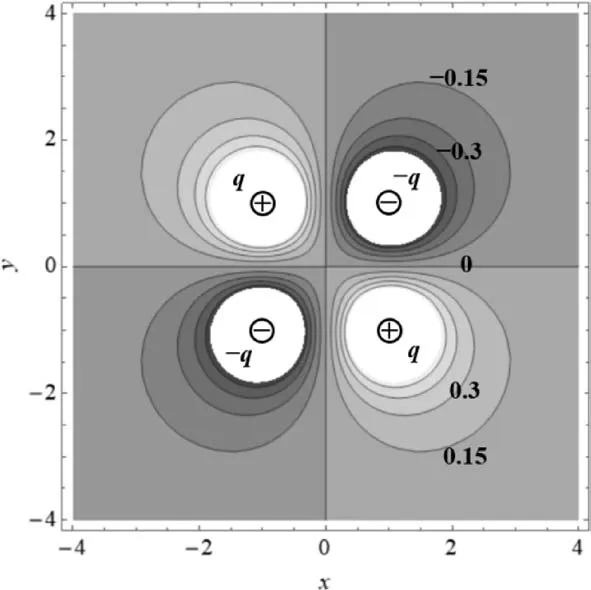
图3

图4

2.2 x Oy平面内的电场分布

使用 Mathematica软件计算（4）（5）式，并利用VectorPlot以及Plot3D命令绘制电场矢量图和电场强度大小变化的立体图，分别如图5、图6所示.

图5

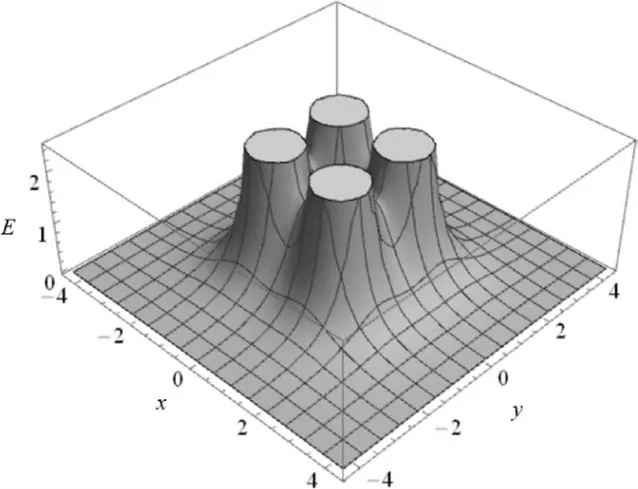
图6

图5显示出电场强度的大小关于正方形的对角线或任意边的垂直平分线（x轴和y轴）对称，但电场方向不相同，对角线上的场强方向沿对角线方向，但方向是变化的.该图还显示了图1中的L和N两点处的电场方向相互垂直，M点的电场方向平行于内切圆在该点处的切线，方向向左，故选项（A）（B）正确.点电荷平面内电场强度大小的分布如图6所示，“柱子”的粗细可以反映该处点电荷电量的大小，此图对应4个点电荷电荷量相等的情况.还可看出在点电荷附近电场强度较大，这也是不难理解的.

3 拓展讨论

以上讨论是正方形一对角线两端是等量负电荷，另一对角线两端是等量正电荷时的电势和电场的分布.现在将点电荷的电性、电荷量、位置进行变化，研究电性、电荷量或位置不同的情况下电势和电场的分布.将电荷量及坐标变化代入前文所得公式（1）（4）（5）中，再利用 Mathematica软件计算并绘制得到对应的电场和电势分布图.

图7和图8是4个等量同号的正电荷位于正方形4个顶点上的电场矢量图和等势线以及电势分布.平面内电势大于0，电势、电场强度大小关于各边平分线和对角线具有对称性.若是4个等量同号的负电荷，除电势为负、电场方向相反外，分布图相似.

图7

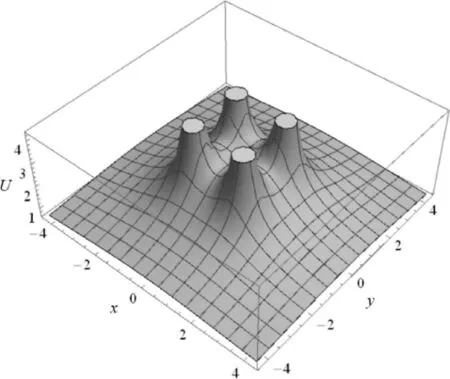
图8

图9和图10是把图1中4个电荷的位置进行调整，对角线上是两个等量异号电荷情形下的电场和电势分布.此时x轴是电势为0的等势线，y＞0区域电势为正.电势关于y轴具有对称性.电场强度大小关于x、y轴具有对称性.

图9

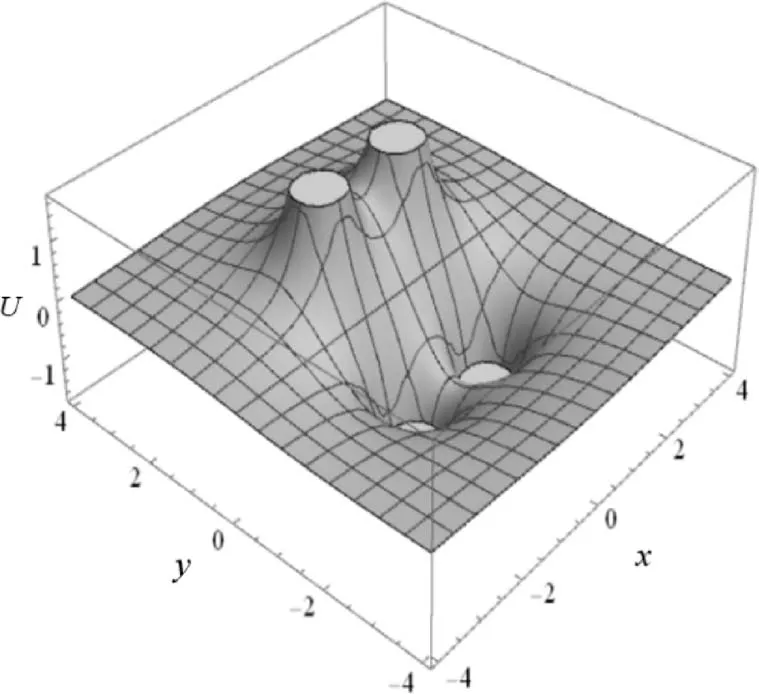
图10

图11和图12是将4个电荷的电荷量进行调整，上面两个点电荷的电荷量为＋2q，下面2个电荷量为－q.此时和图9相比，x轴显然不再是等势线.电势为0的等势线变成了图中的一条闭合曲线，闭合曲线内部区域电势为负.电势、电场强度大小关于y轴具有对称性.

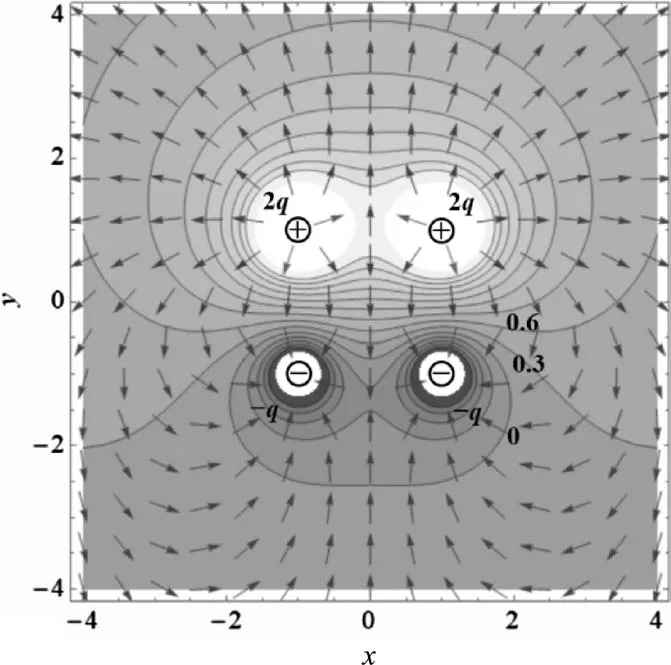
图11

图12

图13和图14是将一条对角线上面两个点电荷的电荷量变为±2q，另一条上的两个点电荷的电荷量变为±q.此时电势、电场不再具有对称性.电势为零的等势线变成了一条倾斜的曲线，曲线下方区域电势为负.

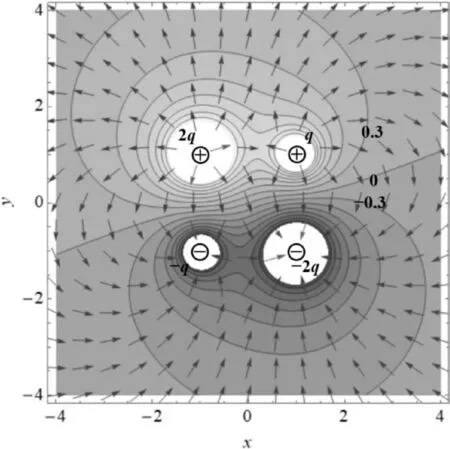
图13

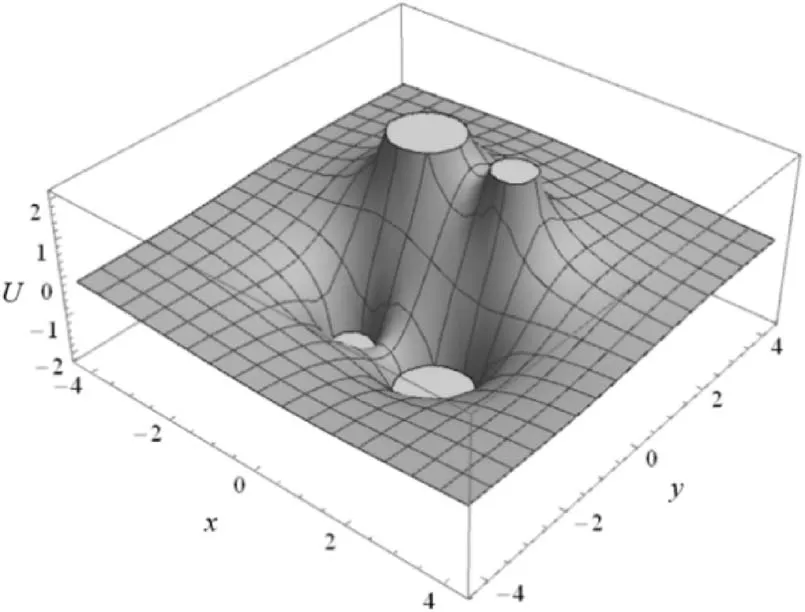
图14

由此可见，当场源电荷分布位置或电荷量发生变化时，空间的电场、电势分布一定随之改变.

4 结论

本文对2022年高考全国乙卷19题中4个位于正方形顶点的点电荷系统产生的电场这一问题，定量计算电场、电势的表达式，并利用 Mathematica绘制其电场和电势分布图，然后进行了拓展，就4个点电荷电荷量、正负电性、位置的不同变化对应的电势与电场分布进行了计算模拟，直观形象地呈现了复杂情形时的电场、电势分布，实现了可视化.模拟结果能够有效帮助物理教师和学生理解位置对称的4个点电荷的电场、电势的大致分布及特点.