基于布鲁姆学习目标和SOLO分类理论的试题对比评析

王贤勇 喻 斌

（贵州省毕节市第一中学，贵州 毕节 551700）

1 相关理论简介

1.1 布鲁姆学习目标分类

布鲁姆学习目标分类最早是由布鲁姆等人于1956年提出的，其主要目的是建构一个详细叙述不同水平认知能力的分类系统，以便在试题命制时能够准确考查考生的认知能力.该分类系统将认知能力分为6种类型，从低到高依次为知识、理解、应用、分析、综合、评价.Anderson把其修改为两个维度，其中一个是知识维度.知识维度分为事实性知识、概念性知识、方法性知识和元认知知识.另一个是认知能力，其中认知能力修改为记忆、理解、应用、分析、综合、评价.［1］本文主要运用的是认知能力维度.

1.2 SOLO目标分类理论

SOLO分类理论是约翰·比格斯和凯文·科利斯在皮亚杰的认知发展阶段理论的基础上提出的，该理论将学生的认知分为5个层次，分别为前结构、单点结构、多点结构、关联结构、拓展抽象结构.对应从点、线、面、立体到系统的发展过程，层级越高，要求学生具备的思维水平或认知能力越高.［2］

1.3 布鲁姆学习目标和SOLO分类理论与“四翼”“情境”学业质量水平的有机结合

中国高考评价体系中提出了“一核”“四层”“四翼”的概念，为高考命题提供了有效的理论支撑.其中“一核”为考查目的，回答为什么考的问题；“四层”为考查内容，回答考什么的问题；“四翼”为考查要求，即“基础性、综合性、应用性、创新性”，回答怎么考的问题.［3］课程标准中明确了学业质量水平，把其分为5级水平，其中水平4是学生进入高等院校相关专业应到达的水平要求.用于高等院校招生录取的水平等级考试试题应具有较好的区分度，有利于区分考生不同层次的学业水平，便于高校选拔人才.［4］下面通过表1和图1呈现它们之间的关系.

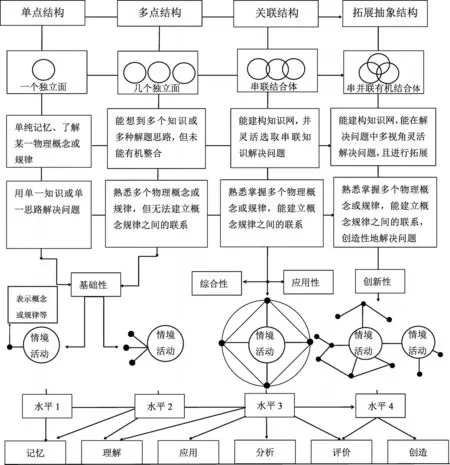
图1 布鲁姆和SOLO理论分类目标与“四翼”“情境”质量水平的有机结合

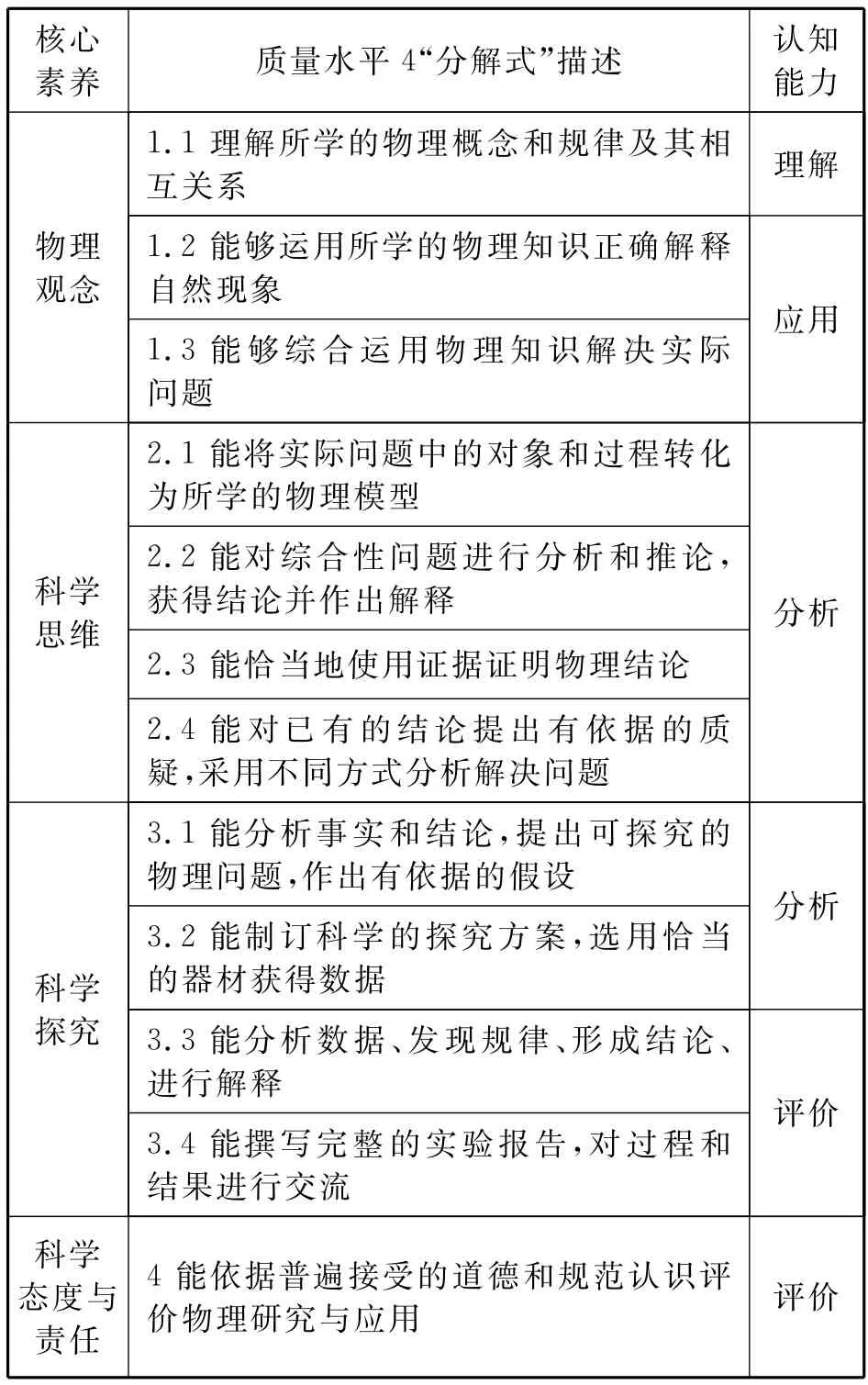
表1 物理课程核心素养、质量水平4和布鲁姆认知能力的对应关系［5］

2 试题对比分析

2.1 试题呈现

题1.（2022年全国高考甲卷第25题）光点式检流计是一种可以测量微小电流的仪器，其简化的工作原理示意图如图2所示.图中A为轻质绝缘弹簧，C为位于纸面上的线圈，虚线框内有与纸面垂直的匀强磁场；M为置于平台上的轻质小平面反射镜，轻质刚性细杆D的一端与M固连且与镜面垂直，另一端与弹簧下端相连，PQ为圆弧形的、带有均匀刻度的透明读数条，PQ的圆心位于M的中心.使用前需调零：使线圈内没有电流通过时，M竖直且与纸面垂直；入射细光束沿水平方向经PQ上的O点射到M上后沿原路反射.线圈通入电流后弹簧长度改变，使M发生倾斜，入射光束在M上的入射点仍近似处于PQ的圆心，通过读取反射光射到PQ上的位置，可以测得电流的大小.已知弹簧的劲度系数为k，磁场磁感应强度大小为B，线圈C的匝数为N.沿水平方向的长度为l，细杆D的长度为d，圆弧PQ的半径为r，r≫d，d远大于弹簧长度改变量的绝对值.

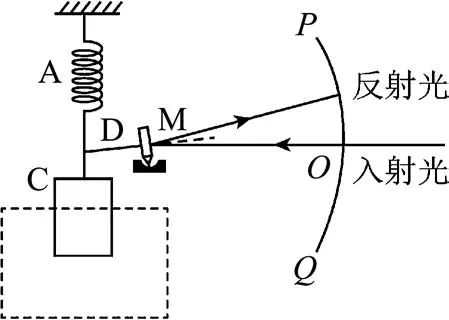
图2

（1）若在线圈中通入的微小电流为I，求平衡后弹簧长度改变量的绝对值Δx及PQ上反射光点与O点间的弧长s；

（2）某同学用此装置测一微小电流，测量前未调零，将电流通入线圈后，PQ上反射光点出现在O点上方，与O点间的弧长为s1.保持其他条件不变，只将该电流反向接入，则反射光点出现在O点下方，与O点间的弧长为s2.求待测电流的大小.

题2.（2022年全国高考乙卷第25题）如图3，一质量为m的物块A与轻质弹簧连接，静止在光滑水平面上.物块B向A运动，t＝0时与弹簧接触，到t＝2t0时与弹簧分离，第一次碰撞结束，A、B的v- t图像如图4所示.已知从t＝0到t＝2t0时间内，物块 A运动的距离为0.36v0t0.A、B分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞，之后A再次滑上斜面，达到的最高点与前一次相同.斜面倾角为θ（sinθ＝0.6），与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求

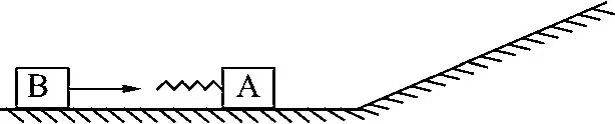
图3

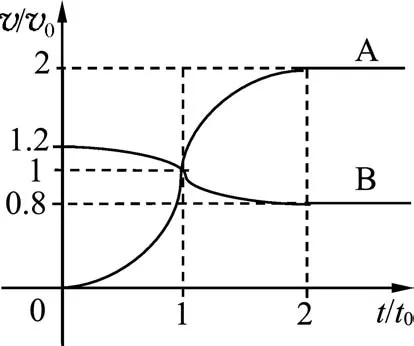
图4

（1）第一次碰撞过程中，弹簧弹性势能的最大值；

（2）第一次碰撞过程中，弹簧压缩量的最大值；

（3）物块A与斜面间的动摩擦因数.

2.2 试题对比分析

试题对比分析见表2.

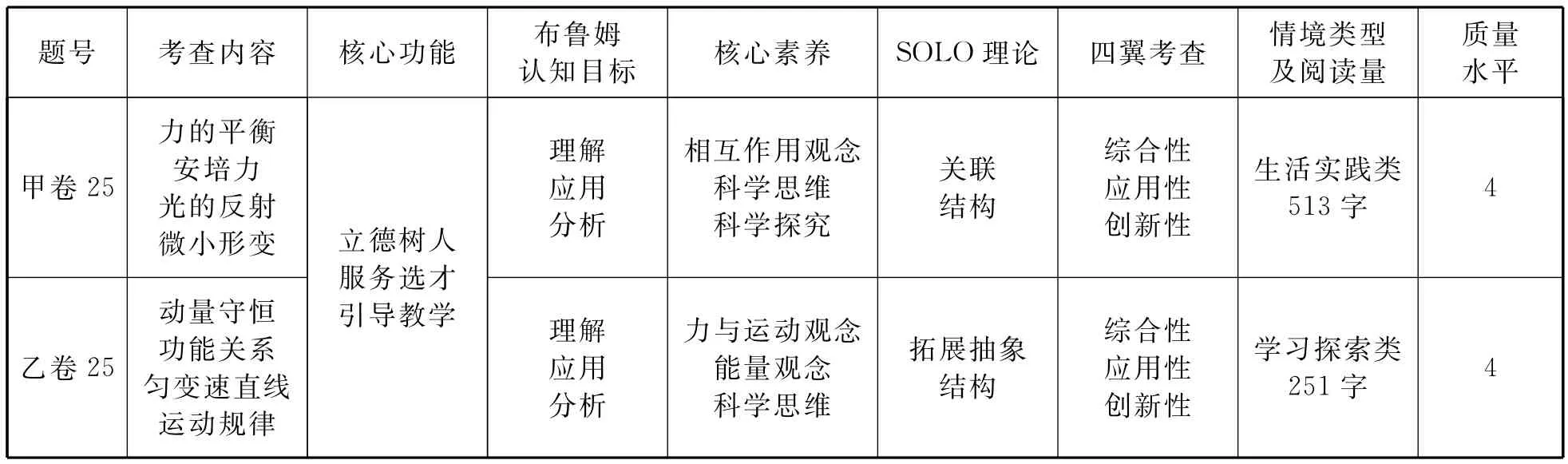
表2 试题对比分析

3 试题详细分析

3.1 甲卷第25题分析

3.1.1 情境化试题分析

如图5所示，该题只包含一个情境，即线圈C（下文简称C）通电后导致弹簧A（下文简称A）的长度发生微小形变，因而与弹簧连接的轻质杆D（下文简称D）带动平面镜M（下文简称M）发生微小转动，最终导致经过平面镜反射的光到达读数条PQ（下文简称PQ）上的位置发生改变，从而得到不同的读数.此题虽然只有一个情境，但是考生要理解该情境非常困难，原因是该题情境描述文字太多，导致部分考生心理压力过大，阅读后无法提取关键信息，故而无法将信息转化为模型来解决问题.本题共有513个字，其中用于情境描述的文字就达到359个.且每一段文字所描述的信息都非常重要，且相互关联.考生要能在有限的时间解决该题，必须做到：（1）要理解轻质模型的特点.知道D与M的连接为固连（定杆模型），与A的连接为可转动连接，一般简称为动杆模型.因为D、M均不计质量，所以M与底座之间无弹力，C通微小电流后弹簧始终保持竖直.（2）C通电后导致D、M和反射光转动，反射光转动的角度是D（M）转动角度的两倍.这里利用了微小量放大的思想方法.（3）C通电平衡后A长度改变量的绝对值Δx只与安培力的大小有关，简化为二力平衡，即kΔx＝NBIL，可以不用分析C的重力.（4）通过圆弧PQ的半径r远远大于细杆D的长度d，d≫Δx的条件，利用极限思想，得出D和发射光转动的夹角均满足正切值等于正弦值，从而找到Δx与弧长s的关系，突破情境化问题的难点.（5）第（2）问必须在第（1）问的基础之上才能完成.第（2）问实际是考查误差分析.有的考生可能会先把偏差值设出来，再利用第（1）问的结论，最后消掉偏差，用这种方法求解的学生比较多.思维层次高、认知能力强，已经把握此题本质的考生会采用等效思维.等效为待测电流作用下正确读数为s1，电流反向后的读数为s2，直接利用第（1）问的结论便可求出结果.能等效的原因是两次未通电前偏差一样.如果通电后第1次的正确结果是示数减去偏差值，那么第2次的结果就是示数加上偏差值，相加即可消除偏差.当然从时间上来看两种解法相差不大，但是可看出采用第2种方法的考生其认知能力还是要强一些.

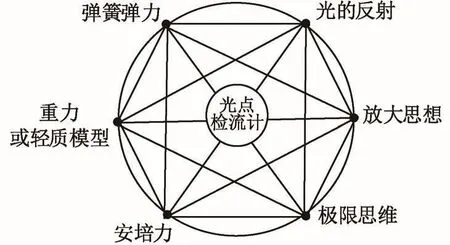
图5

3.1.2 参考答案分析

此题共两问，得分点如下：（1）写对安培力的公式，即F＝NBIL.（2）写对安培力与A增加的弹力的关系，即kΔx＝NBIL，或线圈所受的重力、弹力及安培力的关系.（3）利用极限法写对d、Δx、s之间的关系.（4）得出正确的结果.从给分点来看，此题只需要8个左右关系式（对应得分点）即可得出结果，运算量小.但是对阅读理解能力、思维灵活性、独特性、创新性、要求极高，即要求考生具备很强的关键能力.

第（1）问中，对安培力的公式和kΔx＝NBIL的考查体现“一核四层四翼”的基础性.但得分较低，因思维定式，考生容易漏写N而失分.接下来是考查极限思想、用数学解决物理问题的能力，体现“一核四层四翼”的综合性、应用性，得分更低.第（2）问基于第（1）问考查应用性、创新性，两个关键得分点，由于与第（1）问关联性强，得分率就更低.

可见，此题考点相对单一，能选拔出阅读能力强、心理素质好、思维层次高的考生，但对思维层次中等左右和较低的学生没有区分度.第（1）问笔者了解到，某省理科考生中，该题绝大部分考生没有作出任何解答，全体考生的平均分才1.09分.这充分说明，绝大部分学生面对这道题无从下手，思维层次中等的部分考生即使认真阅读，但因为文字多、情境陌生、复杂度高，关联性强，也未能提取有用信息来建构模型，从而解决问题.

总的来说，笔者认为此题的创新之处是利用了人教版演示微小形变的实验和探究库仑力大小的思想方法，即放大法.此题要引导教学回归教材，要创造性地使用教材；要引导学生“从生活走向物理，从物理走向社会”，学以致用；能对仪器误差进行分析，得出正确结果.最终真正实现从“解题”走向“解决问题”，避免机械刷题.

3.2 乙卷第25题分析

3.2.1 从情境化角度分析

如图6所示，该题包含了3个情境.第1个情境是物块B在光滑水平面上匀速运动；第2个情境是物块B与物块A挤压弹簧发生弹性碰撞；第3个情境是物块A冲上斜面再返回；然后再次相互压缩弹簧，分离后物块A再次冲上斜面，情境与第2、3个情境相同.此题情境多，关联性强，是考生平时熟悉的学习探索情境.该题整体字数为254个，其中用于描述情境的文字有192个，学生比较容易建构模型来解决部分问题.考生要在有限的时间之内解决此题，必须做到：（1）具备很强力的力与运动的观念和能量观念，即能形成观念，解决复杂问题.物块A、B之间有两次相互作用，第1次与教材呈现的情境是一样的，即运动物体与静止物体发生弹性正碰.第2次在教材的基础上拓展为两个运动物块的一维碰撞，方法一样，但计算量大.（2）通过图像获取信息的能力.例如通过图像获取弹簧被压缩最短的时刻、碰撞前后的速度等信息.（3）从情境描述中获取关键信息的能力.例如题干中：之后物块A再次滑上斜面，达到的最高点与前一次相同.学生要能提取出物块A两次滑上斜面的初速度一样的信息.（4）超强的数学方法处理物理问题的能力.例如物块A返回与物块B发生碰撞，需要很强的计算能力和技巧；通过微元法计算弹簧的形变量的过程，既要具备思维的灵活度，也要具有多物体运动的关联度，即两物体的速度关系、时间关系、空间关系.当然，此题可以通过巧妙地变换参考系来完成，即选其中一个物体为参考系，根据弹簧被压缩和恢复原长具有对称性，结合力与运动的观念、动量和能量观念可求出结果.这种走不寻常的路线的解法，对学生思维的抽象能力、创新能力、变换能力要求更高.

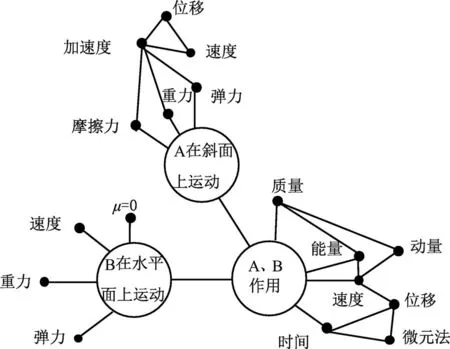
图6

3.2.2 从参考答案的角度分析

该题有以下几个得分点：（1）写出A、B之间相互作用过程的动量和能量守恒，结合图像求出结果，有3个关键得分点.（2）写出牛顿第二定律和运动学中速度和时间的关系，用微元法来处理得出结果，有9个关键得分点.（3）对A、B再次写动量和能量守恒关系，根据A上滑和下滑位移大小相同，写动能定理方程或从牛顿运动定律来求解均可，有5个关键得分点，体现综合性、灵活性.

在此题17个关键得分点中，有10个左右得分点学生比较容易拿到.原因是这10个左右得分点学生平时都比较熟悉.例如用牛顿运动定律来解决问题考生非常熟悉，一维弹性碰撞中动量守恒和能量守恒的方程，只要熟悉理解教材中推导出的结论或熟悉推导思路，均可快速解决部分问题，体现“一核四层四翼”的基础性.余下的7个点得分率低.要用微元法求位移，思维层次要求高.考查学生在熟悉的情境中进行创新，设计非常巧妙，体现“一核四层四翼”的综合性、应用性、创新性.这个创新点的设置显然是为了双一流高校选拔出思维层次高的人才.

总的来说，此题可用于引导教学回归教材、关注基础知识和基本规律.引导学生在熟悉的情境中进行思考、创新，创造性地解决问题.

4 启示

4.1 建构解决问题的流程

基于前面的分析，建构解决问题的流程，如图7所示.［5］古人说得好：授人以鱼不如授人以渔.教学的核心是给学生传递思想方法，提升学生物理的核心素养，多年以后，忘记知识以外还能留在学生心中有用的东西，那就是素养.最有价值和意义的教育是在教学中厚植家国情怀，激发学生学习的斗志和兴趣，让学生能归纳出解决问题的思想、方法，且能进行追问、反思、拓展、创新.例如甲卷25题，可以引导学生反思测量前示数不为0的原因；可以用原装置改装来测量磁感强度，把电流刻度转化为磁感应强度，即可读出磁感应强度的值.也可以由该装置的思想，创新出如图8所示的装置.用金属纽丝B把线圈A悬挂起来置于匀强磁场中，在金属纽丝B上固定一平面镜M，在平面镜前方，图中两虚线之间标有刻度，通过反射光落点的位置关系，可以读出线圈A通电后金属纽丝B扭转的角度.设计原理有两个关键点，其一是采用放大的思想方法，其二是根据安培力产生的力矩和金属纽丝的扭转力矩平衡即可测出（微）电流或磁感应强度.与原题25比较，优点是计算简单，避免了极限思想，灵敏度高.教学中像这样的问题可以采用项目式学习来完成.以小组为单元，通过问题导向，引导学生领悟原理，设计实验方案、团结合作，动手制作一个测量微电流或磁感应强度的装置.这样的教学能有效培养学生实事求是的科学态度、拓展创新能力和动手操作能力.

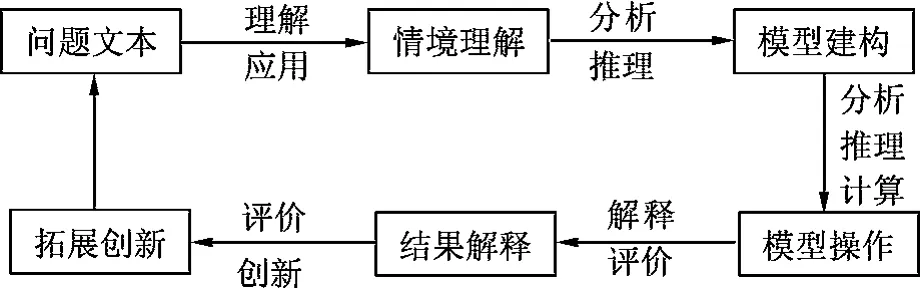
图7

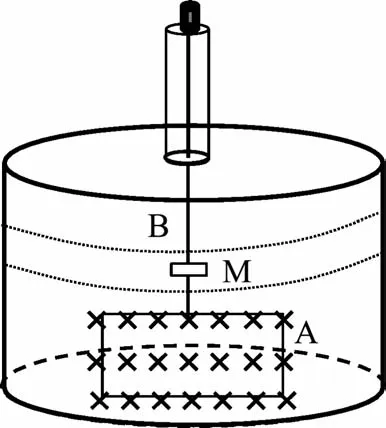
图8

4.2 重视教材、物理课程标准、中国高考评价体系的指导作用

通过前面的表1可以清晰看到，这两道压轴题的核心功能、布鲁姆认知目标、四翼考查都是一样的，说明布鲁姆的认知目标、普通高中物理课程标准和中国高考评价体系为高考试题的命制提供了很强的理论保障，故教师们必须学习分类理论、关注教材、研究课标和高考评价体系.从SOLO分类理论来看，甲、乙卷第25题有差异，甲卷第25题是一个复杂情境下知识的串联结合体，几乎没有主干知识，且知识点相对较少，问题设置独特，学生不易得分.但优点是能引导学生不要盲目背题、刷题；引导教师教学必须关注学生思维的培养、关注学生物理核心素养的提升.乙卷第25题为多情境下知识的串并联有机结合体，问题设置从简单到复杂，在平稳中创新，在创新中发展，层次感强、区分度好，有利于考查出 不同思维层次的考生，有利于不同的高校选拔人才.可见高考试题设置的问题梯度越好，其区分度就越高.

4.3 重视情境、布鲁姆和SOLO目标分类在教学和命题中的应用

当今纸笔考试，情境化命题已成必然，可以肯定地说：无情境，不命题.打开人教版新教材，几乎每一节内容的前面都是通过情境引出问题，然后展开学习的，可见情境的重要性.故教学中也可以这样说，无情境，不教学.良好的情境应基于生活实际，紧扣教学内容、紧扣课标、符合学生认知能力、具有层次性、感知性、探究性、开放性和创新性.

另外，布鲁姆目标分类能让教师从认知能力角度去掌握学生的学习情况，有利于针对性地去提升学生的认知能力；SOLO目标分类能让教师从知识和方法的层级去命制不同质量水平的题目，通过试题的分析也能有效地提升学生的认知能力，从而到达落实物理核心素养的目标.所以教师应加深对这两个理论的学习，并用于实践，指导教学.