静电场教学需注意的几处细节问题

唐伯景

（江苏省昆山中学，江苏 苏州 215300）

本文是静电场教学中存在争议或师生容易疏忽的一些问题，希望通过理论分析和实验探究，能对相关问题的正确处理有所帮助.

1 均匀带电的区别分析

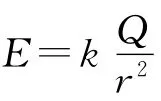
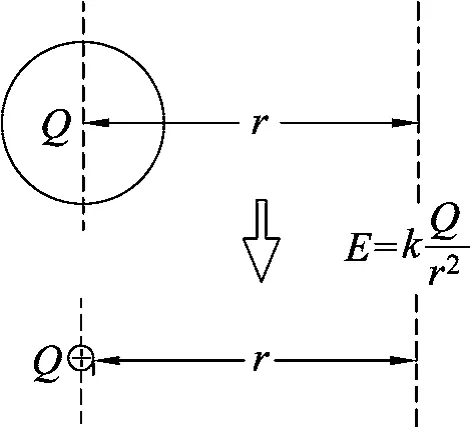
图1 球形带电体与点电荷的等效

因教材没有提及均匀带电球体内部场强是否为0，学生受到前面所学的均匀带电导体球内部场强为0的影响，多认为均匀带电球体内部场强也处处为0.但经过查阅资料，发现均匀带电球体内部场强并不处处为0，学生普遍感到很困惑.事实上，均匀带电球体是指球体内外都均匀带有电荷.如果孤立带电球体是导体，净电荷只会分布在球的外表面，球内不会有净电荷.可见，均匀带电球体应该是绝缘体，不存在因静电平衡而出现内部场强为0的情况.

分析完均匀带电球体，接着我们来分析均匀带电球壳问题.均匀带电球壳无论是导体还是绝缘体，其内部场强均处处为0.借助图2可证明.

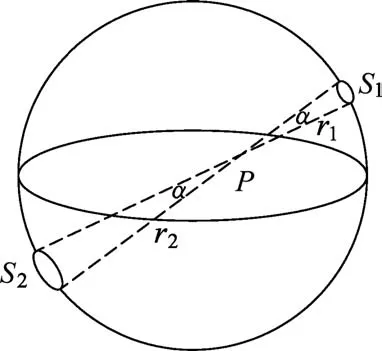
图2

证明：设球壳面电荷密度为σ，如图取同一立体角α两微元曲面S1和S2，对应所带电荷量分别为q1和q2，有

这种情况下，我们无法根据内部场强为0来判断带电球壳是导体还是绝缘体.事实上，若是金属球壳带电，即便不交代电荷均匀分布，其电荷分布也是均匀的；但是绝缘球壳必须交代均匀带电，其内部场强才为0，因为绝缘球壳表面的电荷可能不均匀分布.

分析完均匀带电球体和均匀带电球壳，接着我们来分析均匀带电圆盘问题.由电荷分布的对称性可知，除盘面圆心处场强为0，其余位置场强均不为0.圆盘任一直径上关于圆心对称的两点场强必等大反向，且方向沿该直径平行于盘面.可见，均匀带电圆盘一定是绝缘体.因为若是导体，静电平衡状态下带电圆盘是等势体，其表面处的场强方向应与盘面垂直而不可能与盘面平行.

静电场与物质间存在相互作用，导体和绝缘体由于电学性质不同，它们在静电场中会表现出不同的规律和特征.所以，均匀带电问题的分析处理，首先要根据所给条件正确判断出带电体是导体还是绝缘体.只有这样，我们才能进一步正确分析并得出正确结论.

下面分析2021年江苏高考卷选择题的最后一道压轴题，该题涉及均匀带电.

（2021江苏卷第10题）一球面均匀带有正电荷，球内的电场强度处处为0，如图3所示，O为球心，A、B为直径上的两点，OA＝OB，现垂直于AB将球面均分为左右两部分，C为截面上的一点，移去左半球面，右半球面所带电荷仍均匀分布，则

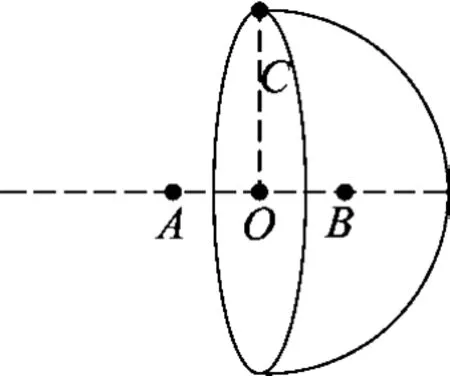
图3

（A）O、C 两 点 电 势相等.

（B）A点的电场强度大于B点.

（C）沿直线从A到B电势先升高后降低.

（D）沿直线从A到B电场强度逐渐增大.

学生学完静电场内容后，笔者借助网课将该题在线上做了一次测试统计.选错的学生很大一部分认为球腔内B点因静电屏蔽场强为0而球腔外A点电场强度不为0，故认为（B）选项正确.出现这样错误选择，主要就是对均匀带电体是导体还是绝缘体这一首要判断工作出现错误.该题涉及到均匀带电，事实上经分析可知，OB所在直线上场强并不处处为0.该题根据对称性以及场强和电势的关系，可判断出正确选项.

解析：整个球面均匀带电，球内电场强度处处为0.所以，右半球面所带电荷在A点产生的水平向左场强EA与左半球面所带电荷在A点产生的场强EA′等大反向，即EA＝－EA′，EA′方向水平向右.因为A、B两点关于球心对称，由对称性可知，右半球面所带电荷在B点产生的场强EB又与左半球面所带电荷在A点产生的场强EA′等大反向，即EB＝－EA′，所以EA＝EB，即右半球面所带电荷在A点和B点产生的场强大小相等方向相同.所以（B）（C）（D）选项均不正确.设右半球面所带电荷在O点产生的电势为φ1，由对称性可知左半球面所带电荷在O点产生的电势也为φ1，即整个球面所带电荷在O点产生的电势为2φ1.同理可设左、右两半球面所带电荷在C点产生的电势均为φ2，则整个球面所带电荷在C点产生的电势为2φ2.由于球内场强处处为0，所以2φ1＝2φ2，即φ1＝φ2，所以（A）选项正确.

2 平行板电容器间插入金属板或电介质板后场强的变化分析

平行板电容器间插入金属板或电介质板，电容器两板间电场强度如何变化？中学教学多是粗略解释，交代不清，这就很容易造成学生对这类问题理解上的偏差，进而造成问题分析上的错误.

问题：如图4所示，与电源断开的平行板电容器间插入电介质板C后，悬挂带电小球的细线的倾角θ如何变化？

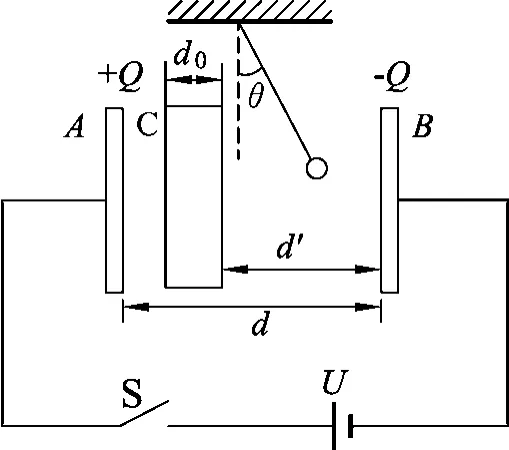
图4

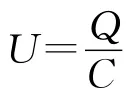
上面的分析是很多学生的通常思路，好像没有问题，但该题的正确答案是悬线的倾角θ不变.

下面借助图4，对平行板电容器间插入金属板或电介质板后，在与电源断开和连接这两种情况下，电容器极板间场强的变化情况分别做具体分析.以下分析涉及的相关物理量符号已在图4中标出.

2.1 平行板电容器与电源断开

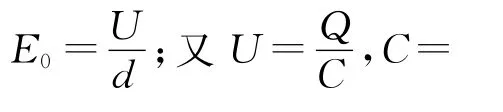
（1）若C板是金属板.

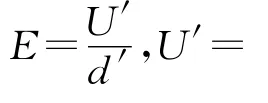
（2）若C板是电介质板.

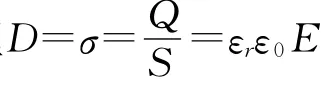
2.2 平行板电容器与电源相连

电容器与电源相连，电路稳定后，电容器两极板间电压U不变.设板插入前，电容器极板间场强为E0.

（1）若C板是金属板.

金属板插入后，设电容器极板与金属板之间的场强为E.静电平衡状态下金属板内部场强为0，由于极板间电压U不变，由U＝E（d－d0），又U＝E0d，可见E＞E0.

（2）若C板是电介质板.

电介质板插入后，设电介质板内部场强为E′，电容器两极板与电介质板间隙中场强为E.因为U＝E（d－d0）＋E′d0，又E′＜E0，可见E＞E0.

综上分析，若与电源断开，无论插入金属板还是电介质板，电容器两极板与所插物体间隙中的电场强度都保持不变；若与电源相连，无论插入金属板还是电介质板，电容器两极板与所插物体间隙中的电场强度都会变大.

中学阶段虽然对电介质的极化现象和高斯定理不作要求，但教学实践表明，定性说明极化电荷的存在及其造成的部分削弱电场效果，这一点中学生不难理解，再结合电场强度与电势差的关系，就能正确分析出电容器两极板间电场强度的分布情况.

3 平行板电容器既定结论的修正分析

“与电源相连的电容器电压保持不变；与电源断开的电容器电荷量保持不变”，这是学生都知道的关于电容器的既定结论.有关电容器动态问题的处理，通常都是在这两个既定结论的基础上进行后续分析.与电源断开的电容器由于不可能对电源进行充放电，其电荷量保持不变，很好理解.但对于电容器与电源相连这类问题，由于存在充电或者放电的可能，而电荷量不会突变，那么在电容器极板间距迅速改变的情况下，电容器两极板间电压是否恒与电源电压时刻相等呢？

下面分别从理论和实验两个角度来探讨这个问题.

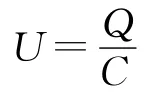
实验探究：如图5，闭合开关S，待电路稳定后，将电容器两极板迅速拉开.接在电容器两极板间的电压传感器显示的电压图像是先增大后减小最后趋于稳定，与电源电压相同.电容器两极板间电压并不是一直与电源电压相等.

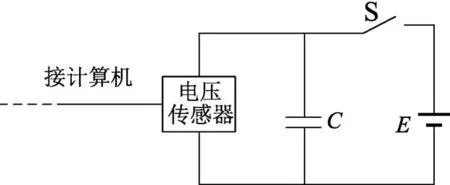
图5

通过上面的理论分析和实验探究，可见通常所讲的“与电源相连的电容器两极板间的电压与电源电压相等”，这是电容器充放电结束达到稳定状态时的电压关系；而在极板间距迅速改变的过程中，电容器两极板间电压时刻改变，并不是通常结论中的保持不变.