基于流量规划的液压悬架负负载调速控制

王华帅,张彦斌,李阁强,周 鑫

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.河南工学院 机械工程学院，河南 新乡 453003；3.机械装备先进制造河南省系统创新中心，河南 洛阳 471003)

引言

液压悬架结构在重型运输车车身载重系统中被广泛采用，如运输钢包的自行式框架车、运输船舶节段的自行式液压载重车、运输高铁预制箱梁的运梁车、运架一体机等重型运输车，均采用多轴线液压悬架结构来均衡车辆载荷，从而使车辆能够更好地适应不平路面，防止单点受力过大，对车身结构或地面造成破环[1-2]。各液压悬架通常采用分组并联的方式连接，即将整车液压悬架分为若干组，每组内所有液压缸油口并联，以达到均衡车辆载荷的作用，从而有效提升车辆对不同路面的适应能力。车辆控制系统通过控制各组悬架的同步升降，实现整车悬架的升降控制[3]。

重型运输车悬架液压系统多采用电液比例负载敏感控制系统进行驱动和控制，并配以平衡阀来实现负负载的平衡和调速，平衡阀既起到平衡负载又起到节流的作用。受车身载荷及悬架姿态变化影响，悬架下降速度常出现不稳定、不均匀问题，单组悬架下降速度的不均匀、不稳定将引起多组悬架同时下降时的不同步，进而造成车辆液压冲击及偏载现象，严重影响设备的使用安全，因此有必要对液压悬架负负载调速控制进行研究。

单组悬架下降速度的控制特性在很大程度上依赖平衡阀的输出流量特性。部分学者从优化平衡阀结构参数的角度研究了平衡阀输出流量特性的优化方法，分析了平衡阀阀芯结构、弹簧刚度、弹簧压缩量、先导比等参数对平衡阀输出流量特性的影响,并指出一组匹配合理的平衡阀参数对负负载系统的调速特性非常重要[4-7]。

部分学者从优化平衡阀控制方式的角度对基于平衡阀液压系统负负载的调速稳定性和节能性展开了研究：如HANSEN M R等[8]采用外部独立油源来稳定压差补偿阀的控制腔压力，从而提高负载下降时回路的稳定性；ANNALISA等[9]则采用外部独立油源来稳定平衡阀控制腔压力以提高系统的调速稳定性，并进一步提出利用平衡阀调节执行器速度的两种调速方法：智能平衡阀和智能系统，同时解决了负负载调速的稳定性和节能性问题，为基于平衡阀的负负载调速控制提供了一种新方法。

部分学者从电液系统控制策略的角度展开了研究：如针对多执行器同步控制问题，刘芮葭等[10]提出了一种基于模糊相邻耦合的控制方法，赵静一等[11]提出了一种基于多点输出耦合的模糊PID多缸位置同步驱动控制策略，李胜永等[12]提出一种利用误差反馈的同步控制方案，这些同步控制策略均在一定程度上提高了多执行机构的同步控制精度。针对流量控制元件输出流量不精确等问题，王灏等[13]提出一种双线性插值控制方法，左强等[14]提出了一种流量规划方法，上述方法均有效提高了流量控制元件输出流量的精确性。

上述研究分别从平衡阀结构参数、平衡阀控制方式、控制策略三个角度对由基于平衡阀的液压系统负负载调速性能的优化展开了研究。采用优化平衡阀结构参数的方法实施过程比较繁琐，且由图1所示悬架液压系统原理可知，本研究的悬架液压系统并未充分利用平衡阀的节流特性，因此，采用优化平衡阀结构参数的方法作用有限。采用同步控制策略虽然可以在一定程度上提高悬架调速性能，但控制策略较为复杂，不易在工程中实现，且高的同步控制精度很大程度上取决于单执行器液压系统良好的控制特性。而优化平衡阀控制方式和提升比例阀和伺服阀输出流量精度的控制方法为液压悬架的负负载调速控制提供了一个全新思路，且具有一定的可实施性，因此基于此思路并结合液压悬架液压系统自身特点，提出一种基于流量规划的液压悬架负负载调速方案，以提高单组液压悬架在不同载荷、不同姿态下的负负载下降速度的稳定性和均匀性。

1 液压悬架控制方案

1.1 液压悬架原控制方案

重型运输车液压悬架控制系统原控制方案如图1所示，悬架顶升过程中，油液由变量泵排出后经压差补偿阀、比例方向阀、平衡阀进入柱塞缸，柱塞伸出，悬架上升。此过程中，油液经平衡阀内单向阀直接流出，平衡阀没有节流作用，悬架上升速度由比例方向阀调节。压差补偿阀能够维持比例方向阀阀口压差为恒定值，提高了比例方向阀输出流量的控制精度及稳定性，单组悬架顶升或各组悬架同步顶升的速度控制精度均能够得到有效保证，因此，控制系统可实现整车悬架顶升速度精确的控制。

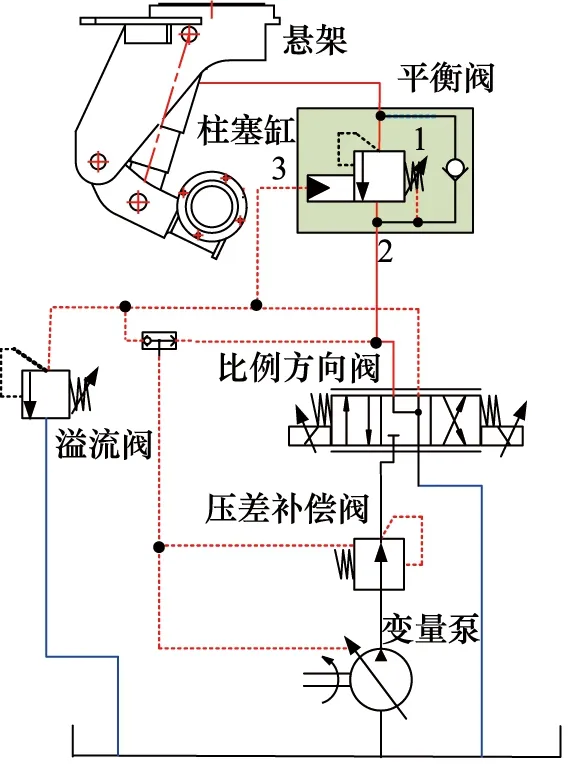
图1 悬架液压系统原理Fig.1 Hydraulic principle of original hydraulic suspension

然而在悬架下降过程中，油液由变量泵排出后经压差补偿阀、比例方向阀、溢流阀后流回油箱，并由溢流阀建立起一定的油液压力作用在平衡阀控制口3处。当平衡阀控制口3处油液压力达到平衡阀开启压力时，平衡阀开启，在负负载作用下，柱塞缸油液经平衡阀，比例方向阀流回油箱，柱塞缩回，悬架下降。此过程中，由于平衡阀3口处的压力基本为定值(溢流阀调定)，平衡阀调节流量的功能不能被充分利用，且由于回油未经压差补偿阀，比例方向阀也不能稳定控制系统回油流量，此时悬架载荷及姿态的变化均将影响悬架下降速度，悬架下降速度存在不均匀、不稳定问题。

1.2 液压悬架新控制方案

为解决悬架下降速度不均匀和不稳定问题，对图1所示回路进行了硬件改进，在图1的基础上增设方向阀、操作手柄、控制器、倾角传感器、压力传感器等元件，并将溢流阀改为比例溢流阀。基于流量规划的液压悬架负负载调速控制方案如图2所示，平衡阀控制油口3由比例方向阀供油，并由比例溢流阀调压，通过调节比例溢流阀的电流，实现平衡阀控制压力的调节，进而实现平衡阀流量的调节。平衡阀的出口并联1个方向阀，悬架下降时，接通方向阀油口，使平衡阀出口2直接与油箱接通，保证平衡阀的进出口压差只与其进口压力有关，消除比例方向阀对回油流量的耦合干扰。同时，在悬架下降过程中，令比例方向阀控制信号u2为一定值，从而控制比例溢流阀溢流量基本不变，保证比例溢流阀的调压稳定性。

图2 液压悬架负负载调速控制原理Fig.2 Negative-load speed regulation control principle of hydraulic suspension

控制系统的控制原理如下：单组悬架在下降过程中，首先，控制器采集手柄指令速度fv和柱塞缸倾角θ，并根据两者计算出平衡阀理论输出流量q1；其次，控制器采集平衡阀进口压力信号p1，并根据流量q1和p1，采取流量规划方法实时计算比例溢流阀的控制电流u3；最后，控制器输出控制电流u2，u3和u4，分别控制比例方向阀、比例溢流阀和方向阀，实时调节悬架下降速度，使其跟随指令速度信号fv，方案控制流程如图3所示。

1.3 新控制方案数学模型

为进一步分析新方案控制原理，在此建立控制方案的稳态数学模型。本研究旨在介绍方案的控制原理，因此在建立控制方案稳态数学模型时忽略了各液压元件的动态特性、液动力、摩擦力、以及油液压缩性等参数的影响。

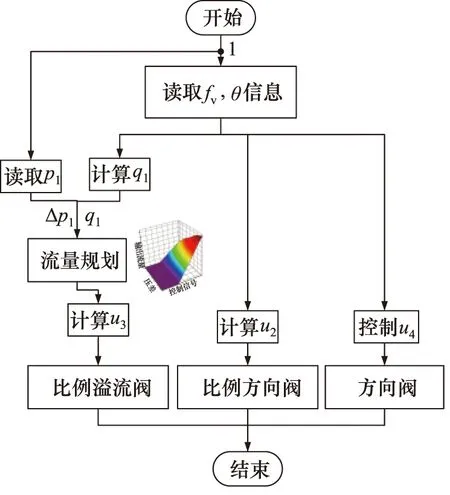
图3 系统控制流程图Fig.3 Flow diagram of system control

比例溢流阀调定压力py满足方程：

py=kyu3

(1)

式中，ky—— 电流-压力增益

u3—— 控制电流

由图4所示平衡阀的结构组成可知，平衡阀阀芯位移xi满足方程：

pyA3+p1A1=kp(xi+x0)

(2)

式中，kp—— 平衡阀弹簧刚度

A1—— 平衡阀进油口1油液有效作用面积

A3—— 平衡阀控制腔3油液有效作用面积

x0—— 弹簧初始压缩量

通过平衡阀的流量q1满足方程：

(3)

式中，Cd1—— 流量系数(常数)

W1—— 平衡阀节流口面积梯度

ρ—— 油液密度

Δp—— 平衡阀进出口压差，且Δp=p1(取平衡阀回油压力近似为0)

联立式(1)～式(3)得到平衡阀流量q1、平衡阀进口压力p1和比例溢流阀电流u3三者之间的关系：

(4)

由式(4)表明，在弹簧初始压缩量x0一定的条件下，q1仅与u3，p1有关，将其关系记为：

q1=f(p1,u3)

(5)

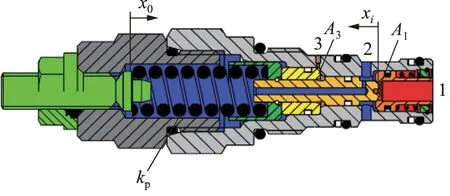
1.进油口 2.回油口 3.控制油口图4 平衡阀结构简图Fig.4 Structure schematic of counterbalance valve

悬架下降过程中，油液由比例方向阀流出后经比例溢流阀建立起平衡阀开启所需控制压力，且压力大小可由比例溢流阀调节，因此比例方向阀输出流量只需大于满足比例溢流阀控制需要的最低溢流流量即可，为获得比例溢流阀最佳调压特性同时兼顾系统的节能性，选取比例方向阀输出流量q2为：

q2=2qymin

(6)

式中，qymin—— 比例溢流阀最低溢流流量

比例方向阀输出流量q2满足方程：

(7)

式中，Cd2—— 流量系数(常数)

W2—— 比例方向阀节流口面积梯度

k2—— 位移-信号增益

Δp0—— 比例方向阀节流口压差

压差补偿阀能使比例方向阀节流口压差Δp0维持一定值，则式(7)可以简化为：

q2=KBu2

(8)

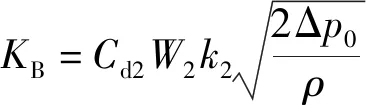
联立式(6)、式(8)可得u2为：

(9)

由图2可知，悬架柱塞缸受力平衡方程为：

(10)

式中，Az1—— 柱塞缸有效作用面积

m—— 负载质量

根据图2所示悬架结构，悬架下降时，柱塞运动方程满足：

(11)

由式(5)、式(11)可建立fv，u3，p1之间的关系：

(12)

由式(1)、式(12)可知，求解控制电流u3，需解出平衡阀进出口压差Δp、控制压力py和平衡阀输出流量q1的关系方程f0(Δp,py,q1)，为分析方便，将方程记为f0(Δp,p,q)。

2 流量规划方法

平衡阀方流量方程f0(Δp,p,q)含有Δp，p和q3个变量，其具体表达式求解较为复杂，且受平衡阀液动力、阀芯摩擦等因素影响，其表达式也不能准确反映三变量之间的关系。因此，本研究基于比例方向阀或伺服阀流量规划的控制思路[13-14]，结合悬架系统的控制特点，提出一种基于平衡阀的流量规划方法：采用线下实验方法预先建立平衡阀的流量映射，得到三变量的一一对应关系，然后根据由控制系统采集并计算求出的Δp和q的大小，进行在线查表或插值，实时求解出平衡阀控制压力p。

第一步：对平衡阀进行线下实验测试，建立平衡阀流量映射关系表。即采样在不同控制压力pij、不同Δpi下的输出流量qj，得到采样点(Δp1,q1,p11)，(Δp1,q2,p12)，…(Δp1,q2,p12)，(Δp2,q2,p22)…。压差Δpi、流量qj和控制压力pij存在一一对应的关系，即pij=f(Δpi,qj)。

第二步：将采样得到的数据点以数据表格形式存储在控制器里，形成1个三维数据表格，将其分别表示为Δp轴、p轴和q轴。

第三步：控制系统在线实时查表和插值计算求解平衡阀控制压力p。

求解平衡阀压差为Δpa、流量为qa时的平衡阀控制压力pa的方法如下：首先通过在线查表找到与点N(Δpa，qa，pa)相邻的4个点N1(Δp1,q1,p11)，N2(Δp1,q2,p12)，N3(Δp2,q1,p21)和N4(Δp2,q2,p22)。

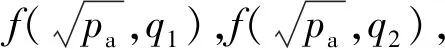
(13)

(14)

最后，沿着q轴，进行线性插值，求出pa：

(15)

联立式(1)、式(15)即可求出比例溢流阀控制电流u3，即：

(16)

3 试验研究

3.1 试验平台

为验证基于流量规划的液压悬架负负载调速方法的可行性，本研究以某型号运梁车为研究对象进行现场实验研究，该型号运梁车液压悬架系统基本参数如表1所示。

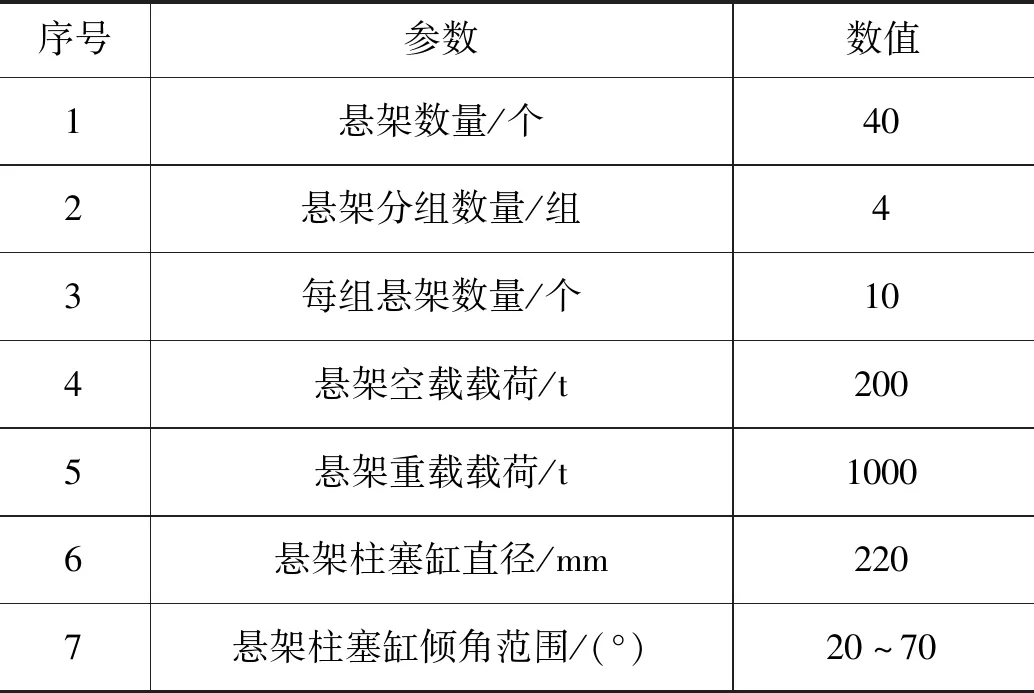
表1 运梁车液压悬架系统参数Tab.1 Parameters of hydraulic suspension system of beam carrier

整车液压悬架共分为4组，每组悬架液压系统组成如图3所示。为研究方便，以其中某1组作为研究对象，其余3组均采用同样的控制方式，从而有效防止运梁车偏载。同时，为获得悬架下降速度参数，在平衡阀出口2处加装流量传感器。悬架控制系统主要元件参数如表2所示。

以上述元件为基础，结合运梁车已有的电控系统，设计出试验方案如图5所示。试验中，该方案采用DEWETron数据采集仪及DEWE-soft软件来进行数据采集和记录。首先，在原方案控制下，采集并记录系统在空载和重载工况下，柱塞缸倾角从70°减小至20°过程中的压力、流量和倾角的变化数据,如图6a、图6b所示；其次，在新方案控制下，同样采集并记录系统在50%控制指令时，空载和重载工况下，柱塞缸倾角从70°减小至20°过程中的压力、流量和倾角的变化数据，如图6c、图6d所示。

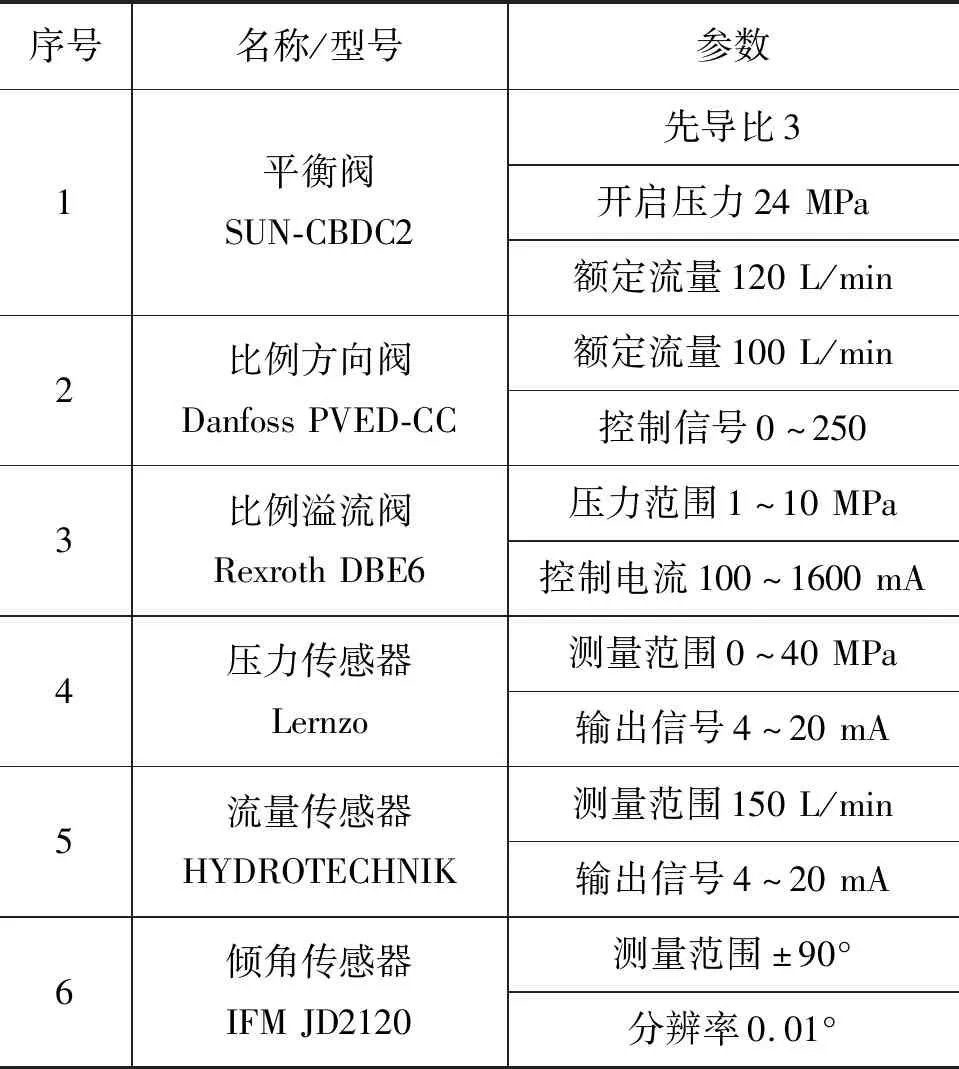
表2 悬架控制元件主要参数Tab.2 Main parameters of suspension control components

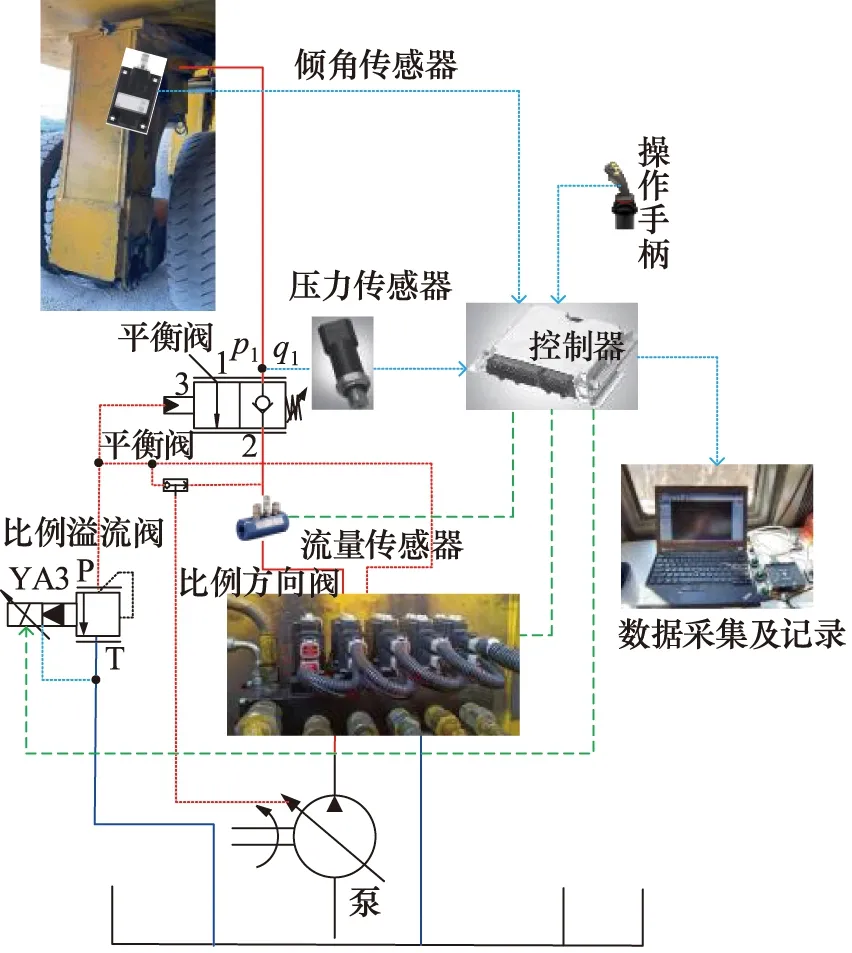
图5 实验原理简图Fig.5 Schematic of experimental principle

3.2 实验结果分析

利用图6所示的流量和倾角等数据，依据式(11)分别计算出在原方案和新方案控制下，悬架在空载/重载工况下的下降速度。原方案控制下的速度曲线如图7a所示，新方案控制下的速度曲线如图7b所示。

为定量分析悬架下降速度的变化，取悬架下降速度变化率来衡量悬架下降速度的均匀性。悬架下降速度变化率为悬架平稳下降阶段(如图7a中A1B1、A2B2段或图7b中B1C1、A2C2段)中某线段两端点速度之差的绝对值与该线段初始端点下降速度的比值。

由图7a可知，原方案控制时，在空载/重载两工况下，悬架下降速度随柱塞缸倾角的变化而变化，空载速度变化率为33%，重载速度变化率为40%，下降速度不均匀。此外，悬架空载/重载最高下降速度相差将近200 mm/min，悬架下降速度受载荷的影响较大，悬架下降速度不稳定。因此，悬架下降速度随悬架姿态和悬架载荷的变化而变化，速度不均匀、不稳定。

但由图7b可知，新方案控制时，悬架系统在A2C2区间内，重载悬架下载速度比较均匀，变化率为15%。在B1C1区间内，空载悬架下降速度也较为均匀，变化率为17%，速度均匀性较好。且在上述范围内，空载最大速度与重载最大速度相差仅为10 mm/min，速度稳定性也较好。但在B1点处，空载曲线发生转折，速度随着角度的减小而快速减小(如A1B1区间段)，此处转折是由于在B1点处平衡阀流量达到了饱和，导致悬架下降速度无法继续跟随指令速度。

为了进一步验证新方案的有效性，给出在不同指令速度下，悬架空载和重载下降速度对比曲线如图8、图9所示。

由图8可知，空载工况下，在0%～70%指令范围内，悬架速度随着指令速度的提升而增加，速度与控制指令成比例，且当平衡阀未达到该指令下的流量饱和点时，悬架均能基本保持匀速运动。但通过饱和点后，悬架速度随着倾角的减小而降低，悬架不再保持匀速运动。且在悬架下降过程中，平衡阀流量饱和点发生位置随控制指令的变化而变化(如图8中ABCDEF点)，控制指令越大，流量饱和点发生时的悬挂油缸倾角越大。当控制指令大于90%时，平衡阀流量饱和点移到最大倾角处附近，此时悬架从下降开始便出现流量饱和，悬架下降速度不再受指令控制。

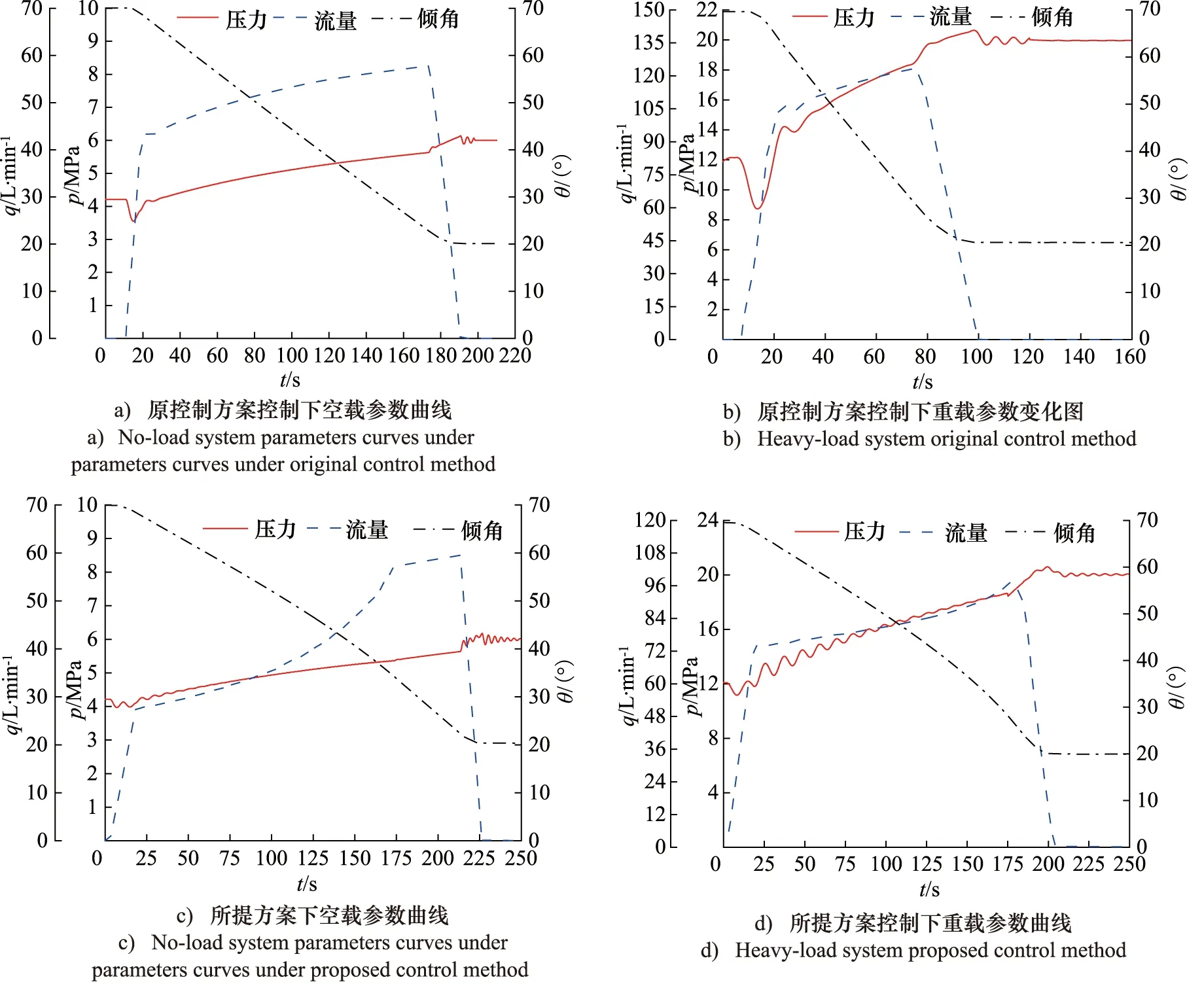
图6 不同控制方案下系统参数对比曲线Fig.6 Contrast system parameter curves under different control method

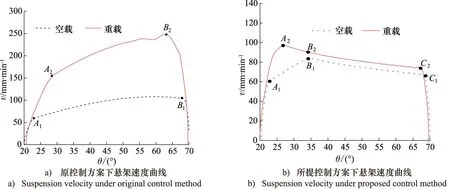
图7 不同方案控制下悬架速度对比曲线Fig.7 Contrast curve of suspension velocity under different control method

由图9可知，重载工况下，悬架速度随着指令速度的增大而增大，且在0%～100%控制指令的范围内，悬架均能基本保持匀速运动，实现了悬架下降速度与指令速度成比例的控制。同时，在整个控制指令区间内，平衡阀均未出现流量饱和现象，由此可知，在平衡阀未发生饱和工况下，新方案能够有效提高悬架下降速度的均匀性和稳定性，原悬架系统悬架下降速度的不均匀和不稳定性问题得到有效改善。

对比图8、图9可发现，空载悬架最大可控下降速度为100 mm/min，重载悬架可控最大下降速度为180 mm/min，两者相差较大，因此，为同时提高悬架速度的控制精度和悬架下降效率，在后续控制中，控制系统最大指令速度应分模式(空载/重载)设置。

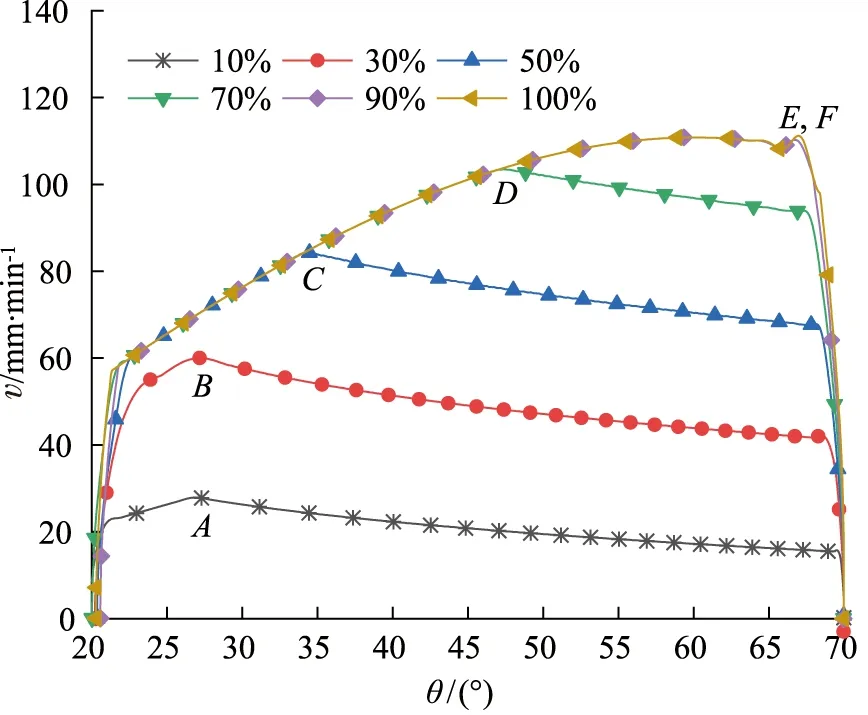
图8 不同指令下空载悬架速度曲线Fig.8 No-load suspension velocity curves with different orders

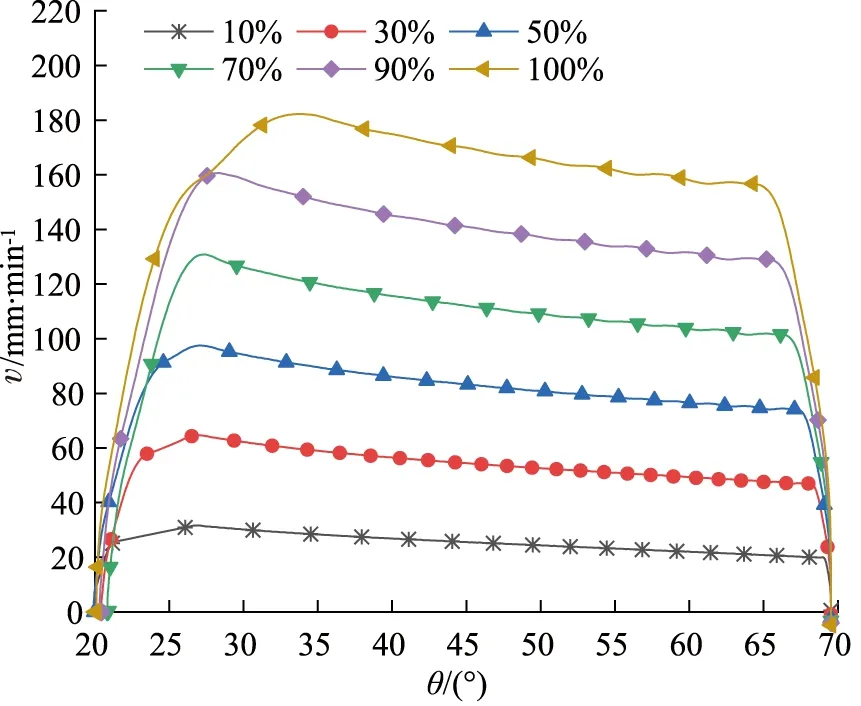
图9 不同指令下重载悬架速度曲线Fig.9 Heavy-load suspension velocity curves with different orders

4 结论

针对液压悬架负负载下降速度受悬架载荷及姿态影响而出现速度不均匀和不稳定问题，提出一种基于流量规划的负负载调速方案，建立了控制方案的稳态数学模型，并以某型号运梁车为研究对象进行对比实验研究，由研究结果可知：

(1) 新方案能够将空载悬架下降速度变化率从33%降至17%，重载悬架下降速度变化率从40%降至15%，悬架下降速度的均匀性显著提高；

(2) 在平衡阀流量不饱和情况下，悬架在空载/重载工况下的最大下降速度之差从200 mm/min降至10 mm/min，悬架下降速度的稳定性显著提高；

(3) 基于流量规划的液压悬架负负载调速控制方案能够为基于平衡阀的负负载调速控制提供一种全新控制思路，具有很重要的工程实际应用意义。

由于悬架平衡阀的流量饱和现象，导致悬架空载下降速度比重载下降速度低，这在某种程度上不能有效满足实际工程的效率需求。因此在后续研究中，悬架平衡阀空载流量饱和问题有待分析和解决，以进一步提高悬架空载下降速度。