基于ANFIS的电磁换向阀寿命预测

郭 锐，何丝丝，叶 欣，刘光恒

(1.航天发射场可靠性技术重点实验室，海南 海口 571126；2.燕山大学 河北省重型机械流体动力传输与控制重点实验室，河北 秦皇岛 066004；3.燕山大学 河北省特种运载装备重点实验室，河北 秦皇岛 066004；4.燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004)

引言

在现代高精尖科技和智能算法蓬勃发展的背景下，寿命预测技术是提高航空航天、高铁桥梁架设等重大工程装备液压系统的运行可靠性、安全性和维修保障率，降低故障率的关键技术，成为当前学术和工业领域的研究热点。液压元件的寿命预测方法常用基于模型和基于数据驱动的方法[1]。基于模型的方法集成物理和随机建模技术，用于评估剩余寿命的分布，探究部件故障模式的发展，但是，需要对系统及其运行条件进行大量假设和参数估计，且故障类型通常随运行工况而变，难以识别[2]。而基于数据驱动的寿命预测方法不需要准确的故障模型，通过传感器获取研究对象的实时状态数据，提取历史运行数据中的隐藏信息，结合多源信息融合技术，综合考虑影响装备使用寿命的磨损、外部冲击、负载及运行环境的变化等因素，模拟退化特性，自动推断隐藏在数据中的因果关系[3]，利用算法获得剩余寿命的参数表征，为实现寿命预测提供了有力的解决方案。

电磁换向阀用于控制油路与执行元件运行方向，通过寿命预测，能够为复杂机电液系统的可靠运行提供重要保障。JIA Z等[4]针对支持向量机输入参数的合理选择，提出了一种液压阀混合预测方法(SA-SVM)，利用SA优化预测模型的输入参数，并反馈到支持向量机模型中进行非参数预测，降低了预测模型中的结构风险，消除了与传统非参数回归模型相关的过拟合问题，提高了预测精度。ZHANG K等[5]着眼于电液流量伺服阀的压力增益、零泄漏流量和lap关键性能指标，提出了一种基于混合多传感器频响函数和叠加系综(ESB(STK))的系统协同PdM框架，通过优化特征子集大小提高分类精度，减少了过度拟合、训练运行时间等不确定性。师冲等[6]针对液压阀泄漏故障信号的非线性、非平稳性、不同严重程度故障信号特征难以辨识等问题，提出了一种改进 MF-DFA 方法提取分型谱参数特征，通过随机森林分类器进行故障模式识别，完成了电液换向阀内泄漏的故障诊断。TANG X等[7]提出了一种卡尔曼滤波(KF)方法，从驱动电流中提取退化信号，通过KF技术跟踪退化速率和退化状态，并采用蒙特卡洛采样和核密度估计来捕获不确定性，具有较高的预测准确性。UTAH M N等[8]提出了一种交流供电电磁阀的故障诊断方法，基于时域和频域分析波形，提取16个特征参数，并用机器学习技术对电磁阀不同操作模式进行分类，同时基于深度神经网络(DNN)完成了故障模式的RUL预测。MAZAEV G等[9]提出了一种基于深度学习的方法，通过将电磁阀的电流特征表示为图像来建模退化过程，采用AdaNet方法从当前特征中自动学习相关特征，减少构建特征和固定神经网络结构建模工作，为电磁阀寿命预测提供了一种新的、有前景的方法。PRAKASH J等[10]将递归量化分析(RQA)应用于流量信号的分析，提取8个特征参数(6个RQA派生特征和2个非线性特征)，利用流速信号的递归图和机器学习技术训练了集成学习、K-最近邻(KNN)和支持向量机(SVM)3种机器学习方法来预测阀的切换特性，具有较高的预测精度。

以上研究表明，当前液压阀的寿命预测领域研究成果丰硕，已经有了较为成熟的应用，但是针对电磁换向阀的研究较少。自适应模糊神经网络在寿命预测领域已经有了相关应用，因此，采用自适应模糊神经网络算法对电磁换向阀进行寿命预测具有可行性，为电磁换向阀的寿命预测方法提供了一种研究思路。

电磁换向阀的退化机理复杂，例如阀芯磨损、弹簧老化和漏磁等，在多重影响因素的耦合作用下电磁换向阀的性能会出现一定程度上的退化，多表现为电磁换向阀压力损失增加及内泄漏量增加。因此，基于恒定应力加速寿命试验获取电磁换向阀压降和泄漏量数据，采用MEEMD多尺度分解测试数据并降噪重构；应用KPCA方法融合特征参数，构建适用于电磁换向阀压降数据处理的ANFIS，实现电磁换向阀的寿命预测，技术路线图如图1所示。

1 电磁换向阀退化评估指标构建

本研究基于排列熵的随机相关性检测，采用MEEMD降噪方法对电磁换向阀泄漏量数据进行模态分解，按照以下流程：

(1) 添加均值为0、幅值为αi的正负的高斯白噪声对n+(t)和n-(t)至原始信号x(t)，处理后结果为：

图1 技术路线图Fig.1 Technology road map

(1)

(2) 噪声处理信号的EMD分解：

(2)

式中，i为白噪声对数，i=1,2,…,Ne。

(3) 均值化处理，对步骤(2)分解得到的N个分量相加后进行平均值计算：

(3)

(4) 筛选异常分量，人为设定1个阈值，再经过模态分解，如果该分量的排列熵超过了人为设定阈值，对所有超过阈值的分量进行选择。

(5) 对筛选出的异常信号，反复进行步骤(1)～步骤(4)的处理，直至获得被认定为稳定的分量IP(t)。

(6) 分离原始信号中的前(P-1)个模态分量：

(4)

(7) EMD分解步骤(6)获得的剩余信号r(t)，得到的结果就是最终的IMF分量：

(5)

引入KL散度法，计算序列的差异。任意序列X={x1,x2,…,xn}和Y={y1,y2,…,yn}，其相关的KL散度值求解如下：

(1) KL距离δ(p,q)和δ(q,p)求解：

(6)

(2) 最终得到X,Y的散度值为D(p,q)：

D(p,q)=δ(p,q)+δ(q,p)

(7)

式中，p和q分别表示序列X和Y的概率分布。

分解后得到的各个固有模态分量(Intrinsic Mode Function,IMF)中存在着可用信息，而由于模态混叠现象的出现，在分解信号中会显示空的IMF分量，因此，通过相关系数来描述两个信息量的关系，相关系数越大，则IMF分量和原始信号的相关性越大，从而检查MEEMD分解后获得的IMF的有效性[11]。相关系数计算方法如式(8)所示：

(8)

式中，x(i),y(i)为待求解的X和Y序列。

将原始信号MEEMD分解后，分别求解所有IMF分量的相关系数R与KL散度值，分别计算各分量相似性序列集合λi=(Ri+di)，i=1,2,…,n。λmax=(Rmax+dmax)为相似性最优解序列，计算得到的γi就是欧几里得距离，γi数值越大，IMF越值得被选取。

i=1,2,…,n

(9)

式中，d为KL散度值，即d=D(p,q)。

2 电磁换向阀退化试验

电磁换向阀寿命试验台如图2所示，包括电机、动力源(柱塞泵)、冷却器、阀块、被试阀等。设置被试电磁换向阀最高工作压力35 MPa，在保证失效机理不变的前提下，对电磁换向阀进行应力水平为37 MPa的恒定应力(压力)加载，采集电磁换向阀4个油口的压力特征数据，进、出油口的流量特征数据。根据JB/T10365-2014中规定，压降大于出厂压降的2.5倍，并且出现了其他形式的损坏或故障，视为该电磁换向阀失效[12]，考虑到电磁换向阀是高可靠性、长寿命元件，且直至试验完成均未发生失效，因此给定阈值压降达到1.4 MPa时作为失效点。

设定电磁换向阀换向保持时间为5 s，根据电磁换向阀样本中标注的开启时间和关闭时间，可以保证在当前的健康状态下，阀芯可以实现完全位移，泵输出的液压油可以完全进入电磁换向阀。试验过程为静态测量，保证试验过程中的入口压力恒定，电机转速保持不变。并且数据采集是持续的过程，在数据采集时，按周期采集100 s的数据采集取平均值，避免了数据采集过程中出现的数据偶然性。

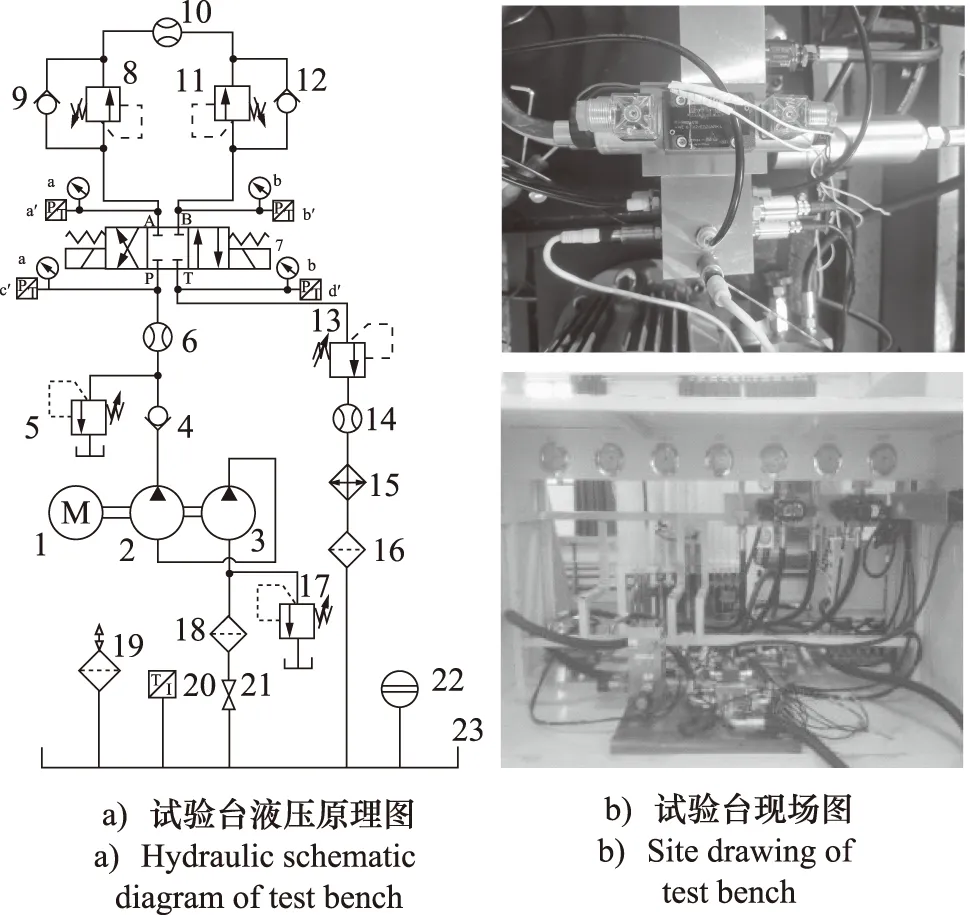
1.电机 2.柱塞泵 3.齿轮泵 4、9、12.单向阀 5、8、11、13、17.溢流阀 6、10、14.流量计 7.电磁换向阀 15.冷却器 16、18.过滤器 19.空气滤清器 20.温度传感器 21.截止阀 22.液位计 23.油箱 a～d.压力表 a′～d′.压力传感器图2 电磁换向阀加速寿命试验台Fig.2 Accelerated life test bench of electromagnetic directional valve

3 电磁换向阀退化模型建立

压降和泄漏量特征数据中蕴含着十分重要的电磁换向阀退化信息，随着试验进程的开展，电磁换向阀换向瞬间的响应速度会随之降低，从时间上看变化不大，但是对于电磁换向阀这类高响应速度的元件，已经出现了性能退化，压降与泄漏量曲线如图3、图4所示。

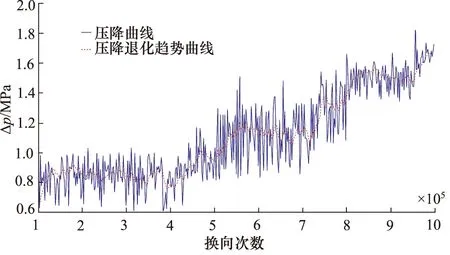
图3 电磁换向阀压降曲线Fig.3 Pressure drop curve of solenoid directional valve

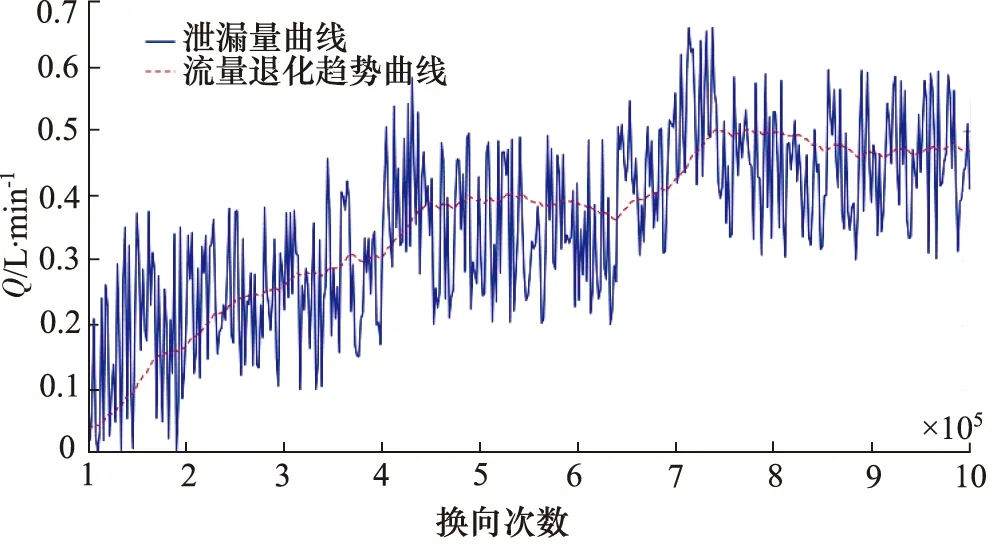
图4 被试阀总流量泄漏Fig.4 Total flow leakage of tested valve

图5 欧氏距离筛选IMF分量流程Fig.5 Euclidean distance screening IMF component flow

将数据进行MEEMD分解和欧氏距离筛选，具体流程如图5所示。含躁信号经过多尺度分解后，得到7个IMF分量，逐一求解各分量的相关系数R,d和欧氏距离，分解结果如图6所示，计算结果如表1所示。

表1 计算结果Tab.1 Calculation results

从数值上可以得出，欧氏距离在IMF5位置处开始收敛趋势，从IMF5位置处开始，往后的模态分量的相关关系下降逐渐减小至0，相反，KL散度数值呈现增长趋势，其数值的倒数也逐渐趋于0。因此利用欧式距离的收敛位置提取IMF分量的方法是可行的。选取IMF1～IMF5为筛选后的有效分量，新的重构信号如图7所示，可以看出，经过MEEMD方法处理后得到了清晰的重构信号。

图6 MEEMD算法分解结果Fig.6 Decomposition results of MEEMD algorithm

图7 MEEMD算法的重构结果Fig.7 Reconstruction results of MEEMD algorithm

首先对MEEMD降重构后的泄漏量信号进行时域、频域、时频域多尺度分析。分别设定MEEMD参数，包括：白噪声幅值Nstd，白噪声对数Ne，嵌入维度m，时间延迟λ，随机性检测阈值θ和最大迭代次数Maxiter。白噪声幅值Nstd和白噪声对数Ne影响了信号的分解效果。一般地，白噪声幅值大小Nstd取信号标准差的0.1～0.2倍，Ne取30～100。嵌入维度m和时间延迟λ决定了排列熵的计算结果，嵌入维度m如果选择数值太小，重构相空间所含状态就会很少，系统的特性无法被完全表现出来；嵌入维度如果选择太大，将会增加算法的运算时间，也会带来额外干扰等问题。嵌入维度m的数值一般选择3～7为宜。时间延迟λ对算法的影响较小，MEEMD分解参数设置如表2所示。

表2 参数选择表Tab.2 Parameter selection

退化指标的构建是以电磁换向阀工作信号的时域、频域、时频域领域内的特征，提炼重构信号的小波包能量、均方频率、峭度等特征，并经过三次指数平滑处理后的特征如图8所示。

通过观察电磁换向阀退化指标曲线发现，随着运行时间的持续，性能退化指标都显露出增长态势，能够在一定范围上表述电磁换向阀的性能退化过程，运用融合算法将提取后的特征进行特征融合处理能够最大限度的发挥各特征参数的表征能力。

图8 电磁换向阀退化指标曲线Fig.8 Degradation index curve of solenoid directional valve

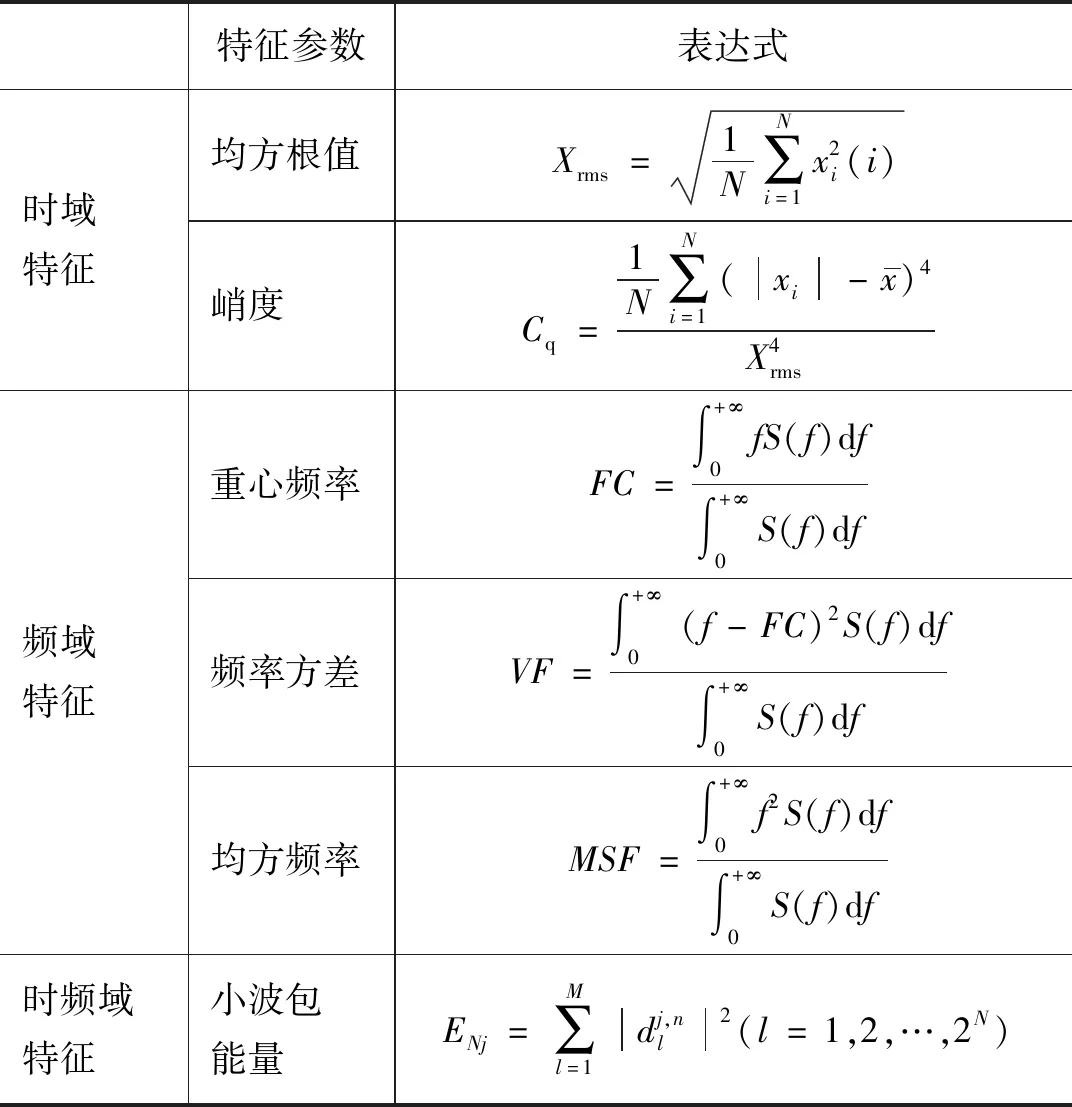
表3 相关特征参数公式Tab.3 Formulas for related feature parameter

KPCA方法是利用引入的非线性函数作为核函数，基于映射的原理，将原始空间转变为高维空间，形成新的数据集合，随后在高维度的数据空间内再次使用主成分分析法(Principal Component Analysis，PCA)进行数据降维[13]，对于非线性信息可以实现更好的数据挖掘。

KPCA的基本步骤如下：

(1) 假设数据集X=[x1,x2,…,xm]，其中x为1个样本，由N个变量组成，m为样本数，x∈R，i=1,2,…,m。

(2) 设定一个非线性映射关系φ(x)：RK→RD，D>>K，样本集X的各个独立向量映射到D维空间，D维空间为高维空间，被记作特征空间F，得到一个新的尺度为D×N的矩阵，新矩阵记作φ(x)：

φ(x)=[φ(x1),φ(x2),…,φ(xN)]

(10)

(3) 计算φ(x)在特征空间F的协方差矩阵CF：

(11)

(4) 在特征空间F中引入矩阵K={Kij}N×N，矩阵K就是核对称矩阵，内积变换求得的新核对称矩阵为：

K=[φ(xi),φ(xj)]

(12)

(5) 在特征空间F中计算所有的主元tk(k=1,2,…,N):

(13)

通过KPCA方法融合特征参数后，按照大小关系排列贡献率，得到的总贡献率变化趋势如图9所示。

图9 总贡献率变化趋势图Fig.9 Change trend of total contribution rate

总体贡献率越高，代表该主成分包含的原时间序列空间信息越多。主成分的选取规则是：总体贡献率低于95%，前两个成分总体贡献率符合条件。提取主成分并平滑处理后，得到对应的退化融合指标[11]，如图10所示。

图10中所示退化融合指标1序列的抖动相对于退化融合指标2更大。在1.5×105～2×105次范围内，退化融合指标2形成了明显的波峰，相对应压降曲线的最低点，见图中矩形框。随着电磁换向阀压降的上升趋势，退化融合指标2呈现着相反的下降趋势。退化融合指标2序列在9.5×105次范围内达到最低点，相对应的位置为压降曲线的最高点。相比退化融合指标2，退化融合指标1波动幅度大，退化融合指标趋势对压降趋势的体现不明显。

4 电磁换向阀可靠性寿命评估方法研究

ANFIS结合了自适应网络和模糊推理系统的模型结构，具备强大的学习能力和模糊推理能力，应用最小二乘法估计和反向传播算法训练模型，经过模糊化、推理和反模糊化处理，输出的结果更加接近实际值[14]。模糊神经网络共有5层组成一个完整的前馈型网络，各层结构功能如下：

(1) 输入层 将各个节点分别直接与输入量分量连接，作为新的输入量传至第2层；

(2) 隶属度计算层 计算各输入分量的相对模糊集合隶属度函数，计算方法如(14)所示：

(14)

式中，a1i,b1i,c1i,a2i,b2i,c2i为ANFIS的前件参数；μAi，μBi为隶属度函数；Ai,Bi为模糊处理结果集合；x1,x2为输入变量。

(3) 规则推理层 匹配模糊规则的前件，得到的结果即为模糊规则的激励强度计算式：

i=1,2

(15)

(4) 归一化与去模糊化层 对网络总体归一化处理：

(16)

对归一化的网络总体模糊化处理，使输出变为精确的结果，计算公式为：

(17)

式中,pi，qi，ri为决定隶属度函数的后件参数。

(5) 输出层 计算整个网格的最终输出结果，表达式为：

(18)

从上节的退化融合指标图中可以看出，退化融合指标经过平滑处理后线性度要高于实际的压降曲线，这是因为融合了其他特征的退化指标，更好地提高了指标的抗干扰能力。

选用三次指数平滑预测算法对获得的退化评估指标1和2进行退化趋势预测，预测阶段为7×105～10×105次，见图11中矩形框。

从预测曲线来看退化融合指标2的预测结果与实际指标的趋势线重合度较高，没有较大波动。退化融合指标预测误差如图12所示，再一次验证了退化融合指标1预测误差大，对压降信号不敏感。

图10 被试阀退化融合指标与压降曲线Fig.10 Degradation fusion index and pressure drop curve of tested valve

电磁换向阀运行初期，电磁换向阀阀口压降变化不明显，甚至有一定的下降趋势，除了电机转速、液压油温度等外界因素对电磁换向阀压降的影响外，可能是由于在运行初期，电磁换向阀的运行状态逐渐变好，性能较出厂时有所提升。为避免减少电磁换向阀初期阶段对神经网络训练结果的不准确因素，训练集的起始位置要在电磁换向阀最优退化点，最佳退化点的选择应该选择压降曲线出现明显上升趋势的时刻。选取被试电磁换向阀退化融合指标2在3×105～7×105次范围内的平滑数据整合为训练集，输入到自适应模糊神经网络进行神经网络的学习和训练。被试电磁换向阀8×105～10×105次的数据作为测试集输出，预测时长T总=2×105次。

图11 电磁换向阀退化融合指标预测结果Fig.11 Prediction results of degradation fusion index of electromagnetic directional valve

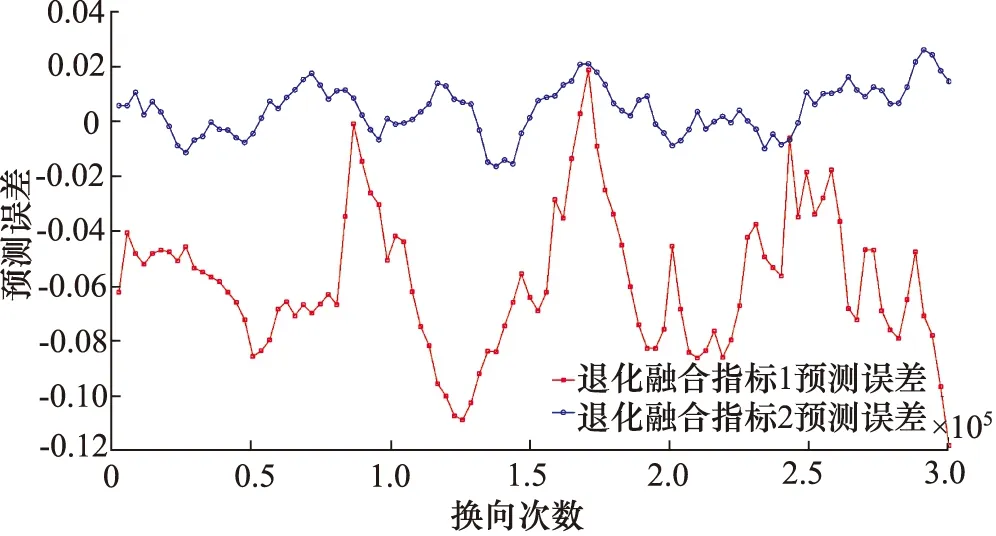
图12 预测结果误差图Fig.12 Error diagram of prediction results

为了比较预测结果，将退化融合指标2的三次指数平滑预测的结果插入到预测结果中进行比较。同样地，应用线性回归模型对压降趋势进行线性拟合，拟合从运行初期开始，在预测起始点处终止，Linear回归拟合模型可表示为：

Y=a1X+a2

(19)

经过回归处理后，被试电磁换向阀线性回归退化模型为：

Y=0.00037X+1.15

(20)

数据训练后的自适应模糊神经网络及其他方法的压降预测结果如图13所示。

从整体趋势上看，预测得到的趋势线与实际运行中的压降趋势线基本符合。由于试验过程中未发生失效，人为设定一个阈值判作为参考判断预测结果的准确性，ANFIS算法的预测结果表明被试电磁换向阀在9.68×105万次时达到阈值，与实际穿过阈值线的实际时间基本吻合；Liner模型预测结果与ANFIS算法有较大差距；三次指数预测算法对电磁换向阀的进出口压降进行预测，虽然从数值上看与ANFIS预测结果相差不大，但是三次指数预测曲线与实际压降曲线有较大差异，所以三次指数预测的结果可能存在着突发性，不应该被用来进行长时间的预测。

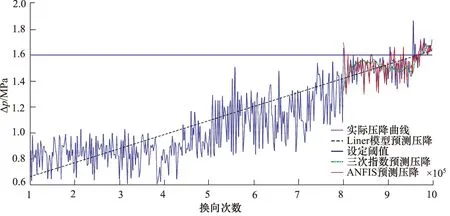
图13 多种方法预测结果图Fig.13 Prediction results of various methods

综上所述，相较于线性模型与三次指数算法，ANFIS方法得到的预测效果更准确，预测趋势更符合实际趋势，ANFIS有着良好的预测效果。

5 结论

以6通径三位四通电磁换向阀的压降和流量数据为切入点，搭建寿命预测试验台，结合仿真结果，重点研究电磁换向阀的寿命预测方法：

(1) 使用改进的MEEMD方法，对仿真信号进行了多尺度分解，以欧式距离的IMFs分量筛选规则完成了噪声信号的重构降噪。应用KPCA方法将特征参数进行融合处理，构建退化评估指标；

(2) 提出了基于ANFIS的电磁换向阀寿命预测方法。基于三次平滑预测对电磁换向阀退化评估指标进行线性预测，利用电磁换向阀的退化评估指标训练自适应模糊神经网络，建立电磁换向阀退化评估模型，有效预测出电磁换向阀的压降趋势，完成了电磁换向阀的寿命预测。