基于普通换向阀的高精度油缸位置控制
何新军,何小群
(1.中冶赛迪重庆信息技术有限公司 智能制造事业部,重庆 401122;2.重庆电子工程职业学院 电子与物联网系,重庆 401331)
引言
传统的电液位置控制基本以伺服阀[1-2]、比例阀[3-4]、高速开关阀[5-6]连续控制介质流量来完成,其阀体结构复杂,对油液清洁度要求较高,价格昂贵。换向阀(Directional Control Valve,DCV)是一种低成本阀门,对环境要求低,控制简单,使用寿命长[7]。实际工程中位置控制多数是点到点的有级调节[8],开发DCV阀控定位控制系统,在保证工艺控制精度的前提下可以有效降低企业的前期项目投资及后期运行维护成本,对企业降本增效具有积极意义。
由于DCV控制的非连续性,开关频率低,以及控制输出的较大时滞,系统普遍存在控制精度不高、系统抖振等问题[9]。目前针对DCV阀控位置控制系统和控制方法的相关研究较少。周创辉等[8]开发了双DCV并联的位置控制系统;金立杨等[9]提出了一种GGAP-RBF神经网络控制方法;郭祥等[10]采用了多个DCV并联模拟伺服阀控制的系统方案。以上文献或采用冗余液压回路、或通过复杂控制算法为DCV位置控制提供了很好的思路。
本研究旨在利用简单液压回路实现油缸定位的精确控制,且算法不宜过于复杂,以便工程应用中一个控制器同时控制多个油缸动作。首先理论分析了DCV开关特性,相平面运动轨迹和液压系统的工作原理,推导了DCV阀控系统的运动方程,提出了一种开关线迭代学习的Bang-Bang控制策略,利用博途PLC平台对油缸运动和控制算法进行了全虚拟仿真,最后在连铸扇形段辊缝控制上实现了生产验证。
1 工作原理
1.1 DCV开关特性
DCV是整个系统的核心控制部件,其开启和关闭时间对阀的动静态特性都有重要影响,直接决定控制系统的稳定性和精度,因此有必要对DCV的开关特性进行分析。图1为典型的螺线管式三位四通电磁换向阀基本结构,由壳体1、2个螺线管2、阀芯3和2个回拉弹簧4组成。
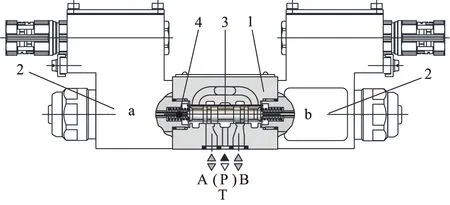
图1 DCV基本结构Fig.1 Basic structure of DCV
螺线管电磁力与回拉弹簧相互作用决定阀芯的开启或关闭,其简单动力学方程[11]:
(1)
式中,Fv—— 螺线管上电后的电磁吸力
mv—— 运动部件质量
C—— 黏性阻尼系数
ks—— 回拉弹簧刚度系数
xv—— 阀芯位移
螺线管电压方程[12]:
(2)
式中,U—— 线圈端电压
R—— 线圈内阻
L—— 线圈电感
I—— 线圈电流
DCV在矩形波激励下的开关动态过程曲线如图2所示[9],电磁铁的吸合和释放过程分成5个工作阶段,对应着阀芯的3个运动过程:
(1) 电气延迟阶段t1当接通电源后,电感L阻止电流增长,当线圈电流增长到开启电流Ion之前,电磁力不足以克服运动阻力,阀芯尚未运动;
(2) 阀芯开启运动阶段t2当线圈电流增大到Ion后,阀芯开始运动。线圈电感附加反电势导致电流反而减小,曲线出现拐点B;
(3) 阀芯到位后停止阶段 阀芯处在最大开启位置xm上,电流重新增长,出现转折点C,直至达到稳态位U/R为止;
(4) 断电延迟阶段t3线圈电感使电流不能突变,阀芯保持开启状态;
(5) 阀芯关闭运动阶段t4线圈电感反电势阻止电流减小,出现拐点E,EF段呈上升趋势,阀关闭后,电流迅速衰减为0,到达G点。
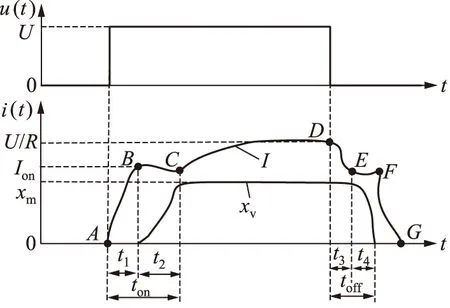
图2 DCV阀芯动态响应曲线Fig.2 Dynamic response curve of DCV
1.2 相平面运动分析
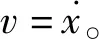
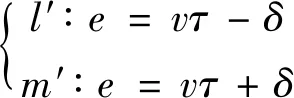
(3)
定义v0为设计速度,正电平u+、负电平u-、零电平u0为控制器输出u的三种状态。当v0>2δ/τ时,u=u+,油缸自A点在相平面上向右运动;到开关线l时,u=u0;实际阀芯关闭滞后使油缸在时间τ内维持v0继续向右运动,直到与有效开关线l′相交于B点,阀芯完全关闭;此时实际速度为0,油缸停止于C点。由于e>δ,故u=u-,系统以速度-v0在相平面上向左运动和有效开关线m′相交于E点,油缸停止于F点。由于e<-δ,故u=u+,重复上述过程。运动系统将沿着相轨迹A→B→C→D→E→F→A描绘出一条封闭曲线,形成半稳定极限环产生极限环振荡。如果v0<2δ/τ,则由A′出发的相轨迹将沿A′→B′→C′→D′而稳定于平衡点。
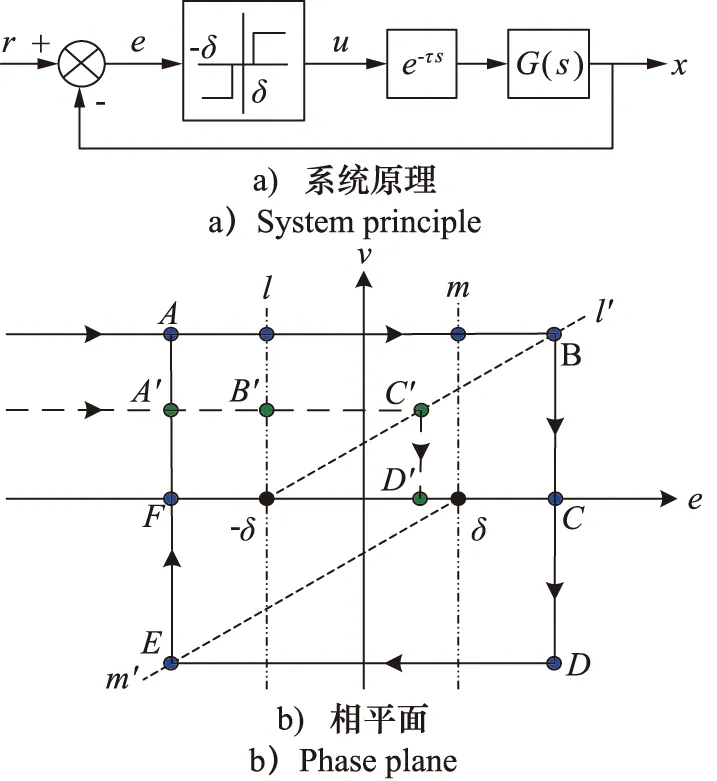
图3 基于DCV的控制系统原理及相平面分析Fig.3 Principle and phase plane analysis of control system based on DCV
综上所述,如果仅以控制精度δ作为开关线,DCV液压位置控制系统的稳定准则为:
(4)
由于控制滞后时间τ是系统固有的,控制精度δ与油缸速度v0呈反比关系。如何保证系统动态响应(不降低运动速度)情况下,提高系统控制精度,将是本研究重点研究内容。
1.3 液压系统工作原理
系统采用DCV作为控制元件,液压缸作为执行元件,节流阻尼孔作为调速元件,液压控制系统原理如图4所示。电磁换向阀1的出油口A,B通过液压锁2及节流阻尼孔3.1和3.2连接到液压缸5的A,B腔;溢流阀4.1和4.2用于保持液压缸压力稳定及高压保护;位移传感器6安装在液压缸5的活塞杆上,用于测量液压缸的实时输出位移。
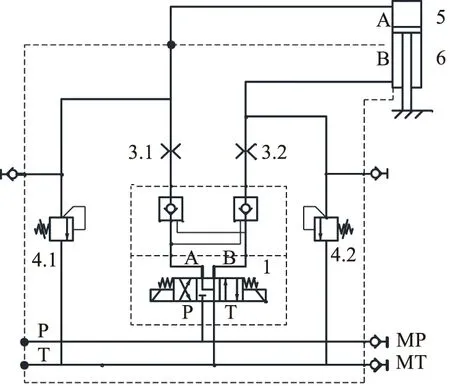
图4 液压控制系统原理图Fig.4 Schematic diagram of hydraulic control system
2 系统方程
2.1 油缸运动速度
下面以油缸活塞上升或下降单向运动描述系统流量方程和油缸运动速度。油液流量QL方程为:
(5)
式中,Cd—— 阻尼孔的节流系数
xv,xm—— DCV的实际阀芯位移和最大阀芯位移
AOri—— 阻尼孔的过流面积
ρ—— 油液密度
ps—— 系统供油压力
pL—— 负载压力
油缸运动速度v为:
(6)
式中,Acyl—— 油缸内腔面积
令系统设计油缸运动速度v0为:
(7)
式中,ΔpN—— 系统设计标称压差
结合式(5)~式(7),则油缸实际速度表示为:
(8)
由于xm,ps,ΔpN,v0均为已知常量,故实际阀芯位移xv和负载压力pL是影响油缸速度的两个主要因子。
2.2 动态阀芯位移
用xv表示时间t时阀芯打开的启动特性,简单模型如下式:
xv=xm·[1-exp(-t/τon)]
(9)
式中,τon—— 阀芯开启运动时间常数
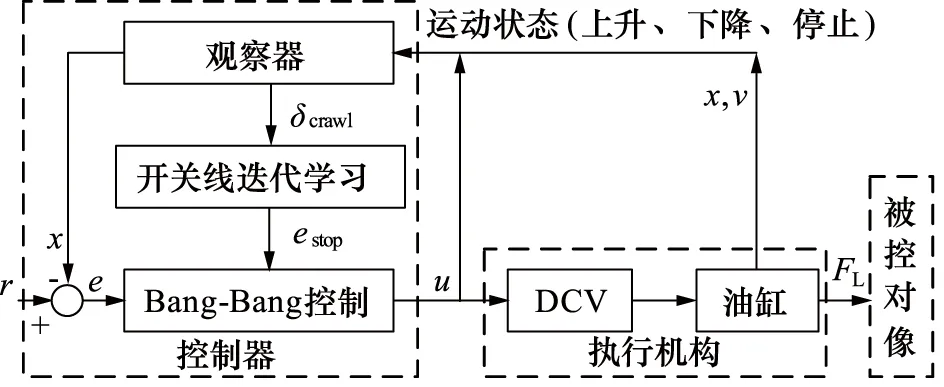
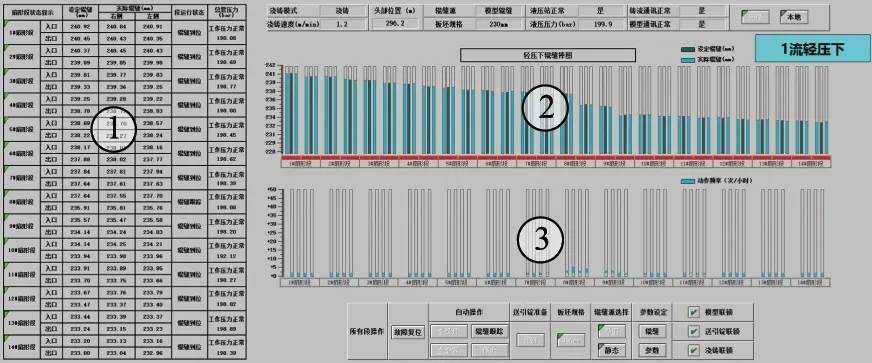
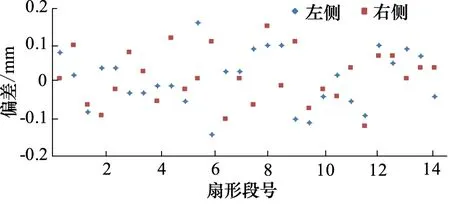
式(9)假定t=0时刻阀芯从静止状态开始启动,实际上DCV通电到阀芯开启还存在电气延迟。令阀芯从通电后延时t=tsta开始开启动作,即t (10) 同理,DCV断电时,阀芯动作也分为两个阶段:断电延迟和阀芯关闭运动。令阀芯断电后t=tstp开始关闭动作,即t (11) 式中,τoff—— 阀芯关闭运动时间常数 本系统采用非对称油缸,其力平衡方程如下式所示: (12) 式中,A1,A2—— 油缸内腔活塞侧和杆侧面积 p1,p2—— 油缸活塞侧和杆侧压力 m—— 液压缸运动部件和负载折算到活塞上的质量总和 B—— 液压缸运动部件和负载的总黏性阻尼系数 k—— 负载的总弹簧刚度 x—— 液压缸的位移 FL—— 作用在液压缸活塞杆上的外部负载力 (13) 同理,油缸上升时活塞侧的负载压力为: (14) 式(8)描述了油缸运动速度;式(10)、式(11)描述了阀芯位移时滞特性;式(13)、式(14)描述了非对称液压缸负载压力求解。以上5个方程式完全描述了DCV阀控系统油缸运动的动态特性,是后续控制策略设计和仿真建模的基础。 控制系统和控制算法如图5所示。u为控制器产生的离散控制信号,由于DCV可以通过2个螺线管(a,b)切换到三种状态,意味着只能对油缸的离散控制信号产生三种输入。基于时间最优原则,常规的Bang-Bang控制[13]可简述为: (15) 图5 控制系统和控制算法示意图Fig.5 Diagram of control system and control algorithm 当|e(t)|≤δ时,Bang-Bang控制系统停止输出,直到误差再次超出控制精度范围。同时,因为控制存在时滞现象,控制信号最小切换时间应充分考虑阀芯开启阶段和断电阀芯关闭阶段的非稳态过程,限制控制信号u的最小切换间隔时间如下式: Tint>Tmin=ton+toff+tothers (16) 式中,Tint—— DCV两螺线管通电的时间间隔 Tmin—— 允许最小时间间隔 ton—— 电磁换向阀的开启响应时间 toff—— 电磁换向阀的关闭响应时间 tothers—— 控制器扫描周期、数字量输出模块及中间继电器响应时间等 (17) 理想的油缸定位控制目标是油缸运动到达目标点,即当动态偏差e(t)小于某个控制精度范围内时,控制信号切换为零电平输出u=u0,此时运动速度v(t) 同时收敛为0。实际油缸运动中,当DCV切换为零电平输出时,实际阀芯不会立即关闭。相平面运动轨迹S(t)如图6所示,此时油缸运动分两个阶段:油缸以初始速度平移滑动,对应DCV断电延迟阶段;油缸减速直至停止,对应DCV断电后阀芯关闭运动阶段。 图6 爬行距离辨识Fig.6 Crawling distance identification 定义DCV断电到油缸运动完全停止这段时间油缸的运动距离为爬行距离δcrawl,如下式所示: (18) 式中,tcrawl—— 断电后到油缸完全停止的爬行时间 vcrawl(t) —— 断电后的油缸爬行速度 由于系统的复杂性和外部负载的不确定性,很难得到油缸爬行的实际运动轨迹S(t)。但在相同的工况和外载条件下,轨迹形状是固定的,爬行距离δcrawl也是有界的,且0≤vcrawl(t)≤v0,v0为系统稳态时的实际速度。设estop为断电时的偏差值,即e(t)=estop为开关线函数,ess为油缸完全停止时的偏差值,则爬行距离δcrawl可以重写为: δcrawl=ess-estop (19) 系统控制目标是,当DCV断电后,油缸爬行一段时间后刚好停止在目标位置附近,由于时滞产生爬行距离是影响最终控制精度的主要因素。因此需要对开关线函数进行迭代学习和调整,使其逐渐趋于爬行距离。本质上,迭代学习控制策略是一类在线优化控制策略,以控制过程中误差趋于0为优化目标。本研究采用结构简单的P型迭代学习控制策略,开关线迭代学习算法为: (20) 式中,k为迭代学习因子。迭代学习因子k的取值对控制器性能有重要影响。若k取值过低,则迭代学习和控制误差的收敛速度变慢;若k取值过大,又会导致控制过程中较大的稳态波动误差,甚至出现振荡。关于k的具体取值,至今没有规范化的学习方法。当控制器结构确定后,k的取值主要取决于被控对象及执行机构的性能。可采用反复实验的方法获取一个合适的取值范围[14]。 引入开关线函数后的改进型Bang-Bang控制算法流程图如图7所示。控制器采用控制死区δ作为跟踪的启动条件,开关线estop作为跟踪的结束条件。每次跟踪仅允许一次DCV状态切换,且完成一次开关函数的迭代学习。当一定时间范围内工况恒定,负载无扰动或呈一定规律性变化条件下,此时爬行距离δcrawl波动较小,本控制算法随着迭代学习次数的增加,可以实现有限时间内系统沿迭代轴的零误差轨迹渐进跟踪。由于油缸的上升和下降设计初始速度和负载条件不同,因此有必要分别对上升和下降设计不同的开关线函数e(t)=-estop+和e(t)=estop-。 这种方法只要考虑控制偏差e(t)和运动速度v(t) 同时收敛为0即可,不用对开关线函数进行复杂建模,从而简化了问题的求解。更重要的是,将一个开环的Bang-Bang控制系统变成了一个闭环的控制系统。 根据工艺控制精度要求设置合理的控制死区δ是有必要的,可以避免油缸定位跟踪过程中控制死区设置过小而反复调整,即“抖振”现象。同时本控制器中采用了开关线迭代学习,可以实现控制误差趋于0的渐进跟踪,定位控制静态误差较小,为跟踪结束后由于液压元器件内泄产生的油缸位置漂移再次超出误差范围提供了一定的缓冲区域,降低了DCV动作频率,减少了DCV频繁开/关产生的瞬态油液介质冲击对油缸或液压阀台密封的损害,从而延长了设备的使用寿命。 图7 改进型Bang-Bang控制算法流程图Fig.7 Flow chart of improved Bang-Bang control algorithm 本研究采用PLC全虚拟软件仿真,其主要优点在于:基于PLC的数学建模可以达到MATLAB的仿真精度[15],且仿真与控制程序都是基于PLC实现,无需花费大量时间集成各个软件包和移植PLC控制程序,仿真结果如图8所示。由于DCV仅能通过开或关间隙式地调节介质流量实现油缸定位,即控制过程中介质流量和速度不可调整,因此仿真实验中仅采用矩形波验证系统的静态响应性能: (1) 参考位置设定和实际位置反馈,参考位置为频率0.1 Hz,幅值2 mm的矩形波; (2) 静态偏差值,定义为DCV断电后油缸完全停时位置设定与实际之差。从图中可以看出,随着开关线整定次数增加静态偏差快速收敛,证明控制算法和开关线迭代学习效果明显; (3) 油缸运动速度,由于系统采用非对称油缸,故油缸上升速度(约1.5 mm/s)和下降速度(约0.9 mm/s)有所不同; (4) DCV控制输出和阀芯反馈,左下角为放大图。 图8 仿真实验中位置控制性能分析Fig.8 Performance analysis of positioning control in simulation experiment 值得注意的是,第一次方波跟踪时,由于开关线尚未整定,油缸上升后超出设定精度范围,故又产生了一次向下运动,即“抖动”现象。控制偏差与开关线函数迭代次数的关系如图9所示,其中迭代学习因子k=0.5,经过开关线函数3~5次迭代学习后,油缸上升和下降的静态偏差迅速收敛,DCV仅切换一次就可以达到较高的控制精度。 图9 控制偏差与迭代次数Fig.9 Control deviation and number of iterations 在扇形段辊缝控制系统中,扇形段使其按照设定辊缝运行,以跟踪铸坯自然收缩厚度和液相穴末端实施轻压下[16],是典型地有级位置调节。连铸生产扇形段布置如图10所示,此条生产线配置有14个扇形段,每个扇形段4个定位油缸,共计56个油缸;每个油缸单独配置DCV阀台和位置传感器,用于调整扇形段辊缝。扇形段辊缝控制监控HMI画面如图11所示。区域①为扇形段入口/出口设定辊缝与4个油缸实际辊缝;区域②为扇形段辊缝跟踪棒图,每组棒图中间表示辊缝设定值,两侧表示左/右2个油缸辊缝实际值;区域③为换向阀的动作频率显示。控制偏差统计如图12所示,辊缝控制偏差小于等于0.1 mm的命中率为89.3%,所有控制偏差均小于0.2 mm;换向阀动作频率较低,均不超过10次/h;整个系统控制稳定,控制精度满足工艺生产需求。 图10 连铸生产线扇形段布置Fig.10 Segment layout in continuous casting production line 图11 实际生产过程HMI画面Fig.11 HMI screen in actual production process 图12 实际生产过程中扇形段辊缝控制偏差Fig.12 Control deviation of segment gap in actual production process (1) DCV开关特性和相平面运动理论分析表明,DCV的时滞特性是影响油缸定位精度和控制系统产生极限环振荡的主要原因,提出了系统稳定判定准则公式; (2) 推导了基于DCV阀控非对称油缸的运动方程式,DCV阀芯动态位移与油缸油液的负载压力是影响油缸运动速度的两个主要影响因子; (3) 针对常规Bang-Bang控制器容易造成的系统“抖动”现象,开发了一种基于观察器和开关线函数迭代学习的改进型Bang-Bang控制算法。在线的开关线函数迭代算法不需要复杂建模,简化了问题的求解,将一个开环的Bang-Bang控制系统变成了一个闭环的控制系统; (4) 最后基于博途PLC进行了仿真研究和生产验证,结果表明,改进型的Bang-Bang控制器可以快速辨识和开关线函数迭代。实际生产过程中,56个DCV阀控系统的控制精度小于等于0.1 mm的命中率为89.3%,全部控制精度小于0.2 mm,DCV动作频率较低,有效降低了对设备的瞬时冲击。整个控制系统控制稳定,控制精度较高,满足连铸生产工艺控制要求; (5) 利用简单、经济的普通换向阀代替复杂、昂贵的伺服阀、比例阀、高速开关阀,实现油缸有级位置调节,在保证工艺控制精度和系统稳定性的前提下可以有效降低企业的前期项目投资及后期运行维护成本,对企业降本增效具有积极意义。2.3 油缸负载压力
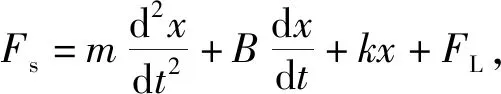
3 控制策略
3.1 控制系统及算法
3.2 开关线函数迭代学习
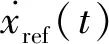
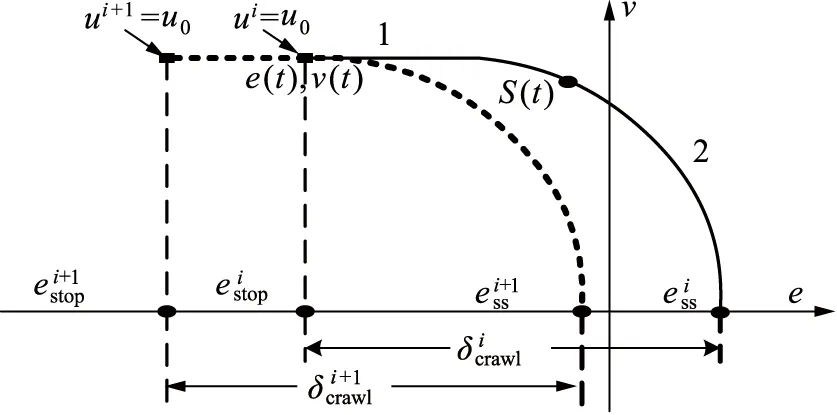
3.3 改进型Bang-Bang控制算法
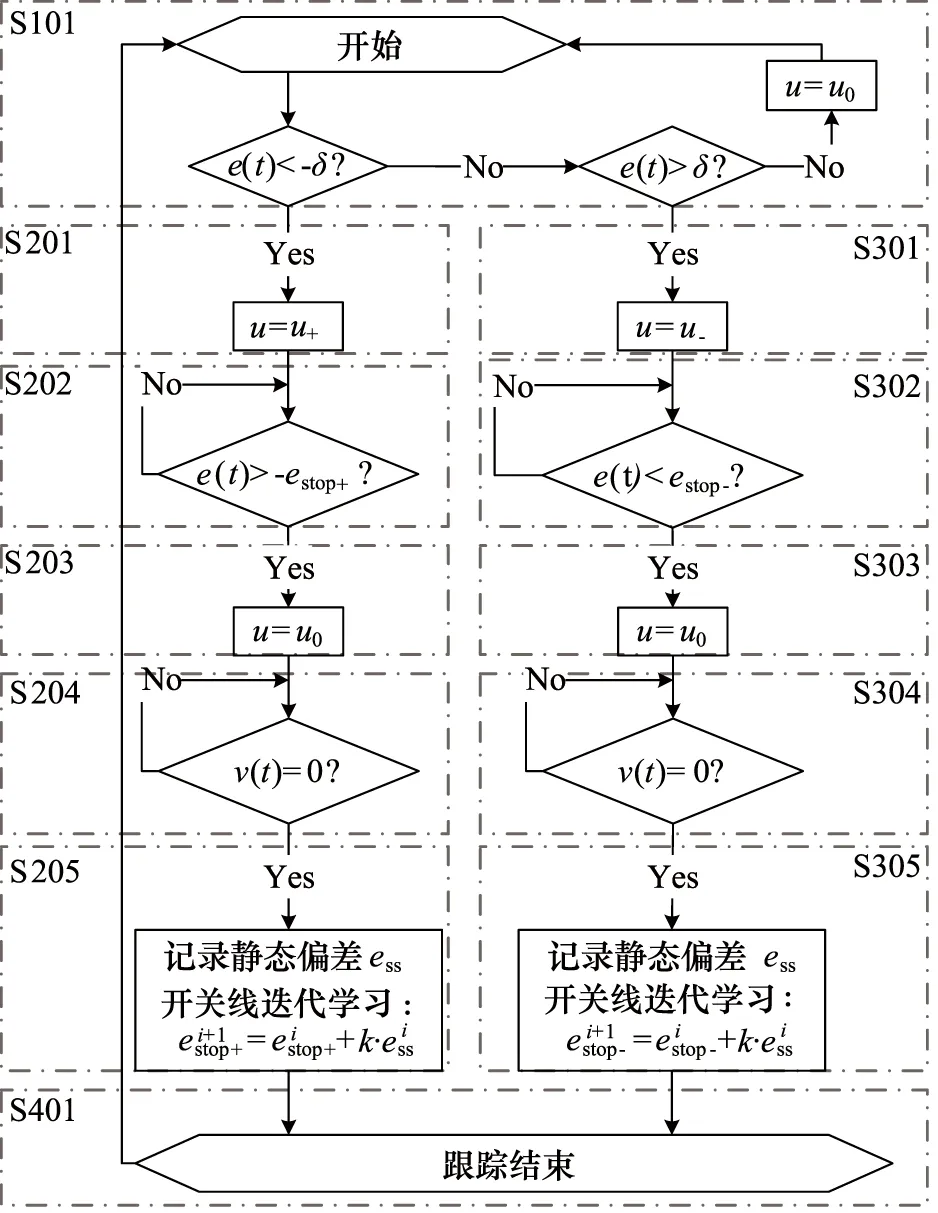
4 仿真分析及生产验证
4.1 仿真分析
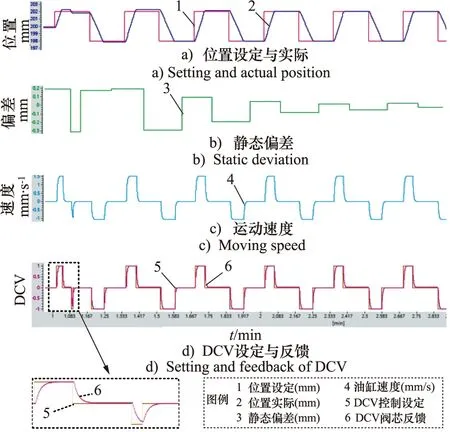
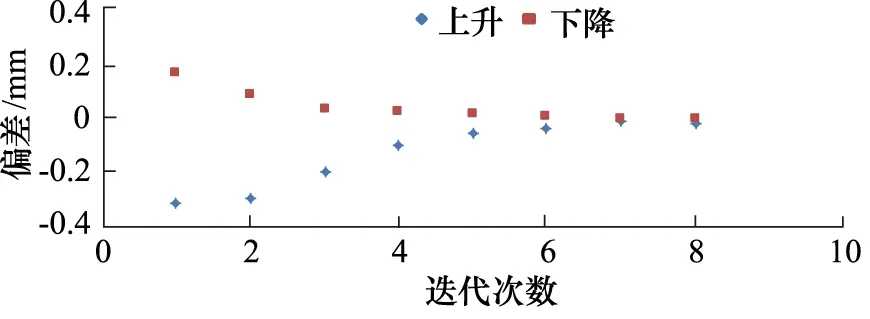
4.2 生产验证

5 结论

