超高压水压泵柱塞副间隙泄漏占比的仿真计算

刘世琦， 冀 宏， 刘银水

(1.兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050；2.华中科技大学 机械科学与工程学院， 湖北 武汉 430074)

引言

超高压水压泵是潜水器装备浮力调节系统的核心部件[1-2]，超高压、水介质条件下的柱塞副间隙泄漏会对泵的容积效率和总效率产生较大影响，因泵的工作环境特殊，能源储存及供应条件有限，因此要求其应具备较高的总效率。如何准确预测和减小柱塞副间隙泄漏量，对超高压水压泵的设计制造有重要意义。

针对柱塞副间隙泄漏的建模、计算等问题，一些专家学者已经进行了研究。胡仁喜等[3]建立了高压高转速下柱塞泵柱塞副泄漏流场的数学模型，认为柱塞副在高压、高转速下处于偏心状态，且实际泄漏量相较于同心状态下泄漏量变化趋势相同。唐辉[4]建立了柱塞副泄漏的数学模型，对倾斜状态下的柱塞副间隙流动进行了理论分析，认为柱塞副间隙较小时，需同时考虑压行程和吸行程，间隙较大时，吸行程泄漏可以忽略，认为柱塞的最小留缸长度只对压行程的泄漏有影响。杨秀峰[5]通过理论分析、正交试验和仿真计算对水压环形缝隙的流场特征和流动规律进行了分析，得到了压力、柱塞直径、密封长度、间隙高度和偏心对环形缝隙泄漏量影响的主次顺序。欧大生等[6]采用有限元和试验结合的方法，考虑柱塞偶件在工作过程中的固体变形，对柱塞间隙泄漏进行分析计算，得到补偿性柱塞偶件能够较大程度改善柱塞副间隙泄漏，提高容积效率。QIAN等[7]建立了高温高压下柱塞偏移时的柱塞副泄漏数学模型并进行了计算，结果表明减小柱塞副初始间隙对降低柱塞副间隙泄漏有重要影响，且柱塞运动速度的增加有助于减少泵送冲程期间的泄漏。苑士华等[8]结合工作压力与温度对油液黏度的影响，得到油液黏度变化下的球塞副泄漏计算公式，结果表明在考虑油液黏度变化时，球塞副泄漏量数值较大，且随压力的增大而迅速变大。何毓明等[9]搭建了滑阀内泄漏仿真模型，计算分析了压力、间隙大小等因素对泄漏的影响，通过正交分析确定了影响程度主次顺序，其中间隙大小的影响程度最大。李元等[10]在经典泄漏公式的基础上，结合Barus油液黏压公式，建立了考虑油液黏度的柱塞副泄漏模型，得出压力达到35 MPa 时油液黏度对泄漏量的影响不可忽略。

上述文献为本研究提供了有益的参考，但考虑水介质黏度、间隙受压形变在柱塞轴向沿程变化下对柱塞副间隙泄漏影响的研究较少。本研究针对超高压水压泵细长型柱塞副间隙，考虑水介质黏度、间隙受压形变在柱塞轴向沿程变化，对工作压力从0～120 MPa变化时的柱塞副间隙泄漏进行了仿真计算，分析了水介质黏度、柱塞副间隙高压形变、柱塞偏心、柱塞副间隙大小及柱塞副接触长度对柱塞副间隙泄漏的影响。

1 柱塞副间隙泄漏理论分析

1.1 细长型柱塞副结构

图1是一种超高压水压柱塞泵结构图[11]，主要包括配流阀组件、柱塞滑靴组件、柱塞套、复位机构和压力补偿器。水压柱塞泵在工作时，通过电机带动主轴做旋转运动，主轴与斜盘固定连接，采用固定强制回程结构，使得柱塞在柱塞套中被迫往复运动，通过配流阀配流，完成吸排水过程。

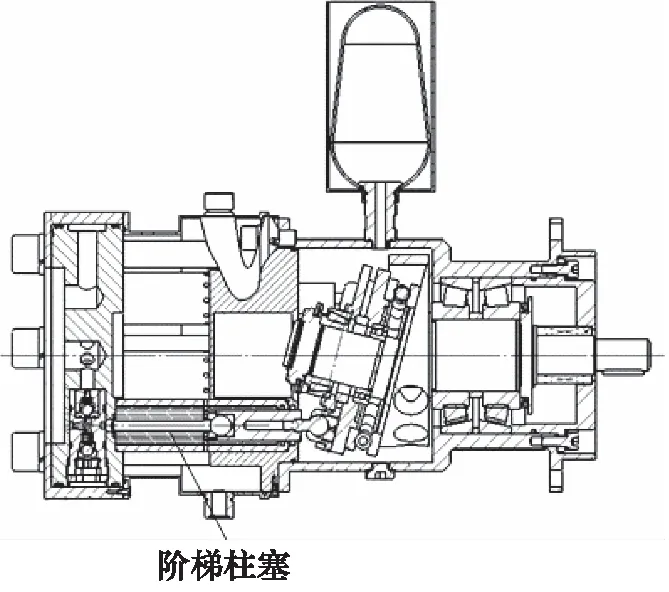
图1 一种超高压水压柱塞泵结构图[11]

本研究的超高压水压泵所用柱塞为阶梯柱塞，由大柱塞和小柱塞组成，大柱塞和小柱塞用球铰连接，如图2所示。

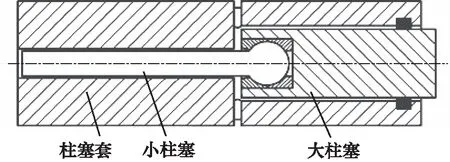
图2 阶梯柱塞结构图

分体式的阶梯柱塞结构，通过大柱塞、小柱塞与柱塞套之间的间隙大小不同，将所受的侧向力转移至大柱塞上，由于大柱塞与小柱塞之间为球铰连接，大幅地减小了大柱塞侧向力向小柱塞传递，因此可以认为小柱塞不承受侧向力、不产生倾斜状态。

由于要在超高压环境工作，超高压水压泵的输出流量相应较小，其排水小柱塞的直径亦较小，为了尽量减小柱塞副间隙泄漏量，增加了小柱塞的留缸长度，因此小柱塞呈现细长型柱塞结构。

1.2 柱塞副间隙泄漏分析

柱塞副间隙泄漏由两部分组成，一是由柱塞副间隙两侧压力差产生的泄漏量，称为压差流；二是由柱塞副相对运动产生的泄漏量，称为剪切流。通常情况下柱塞副间隙大小为微米量级，因此间隙的水力直径较小，同时由于介质存在黏性，使得间隙流动的雷诺数较小，流动状态为层流[12]。

在实际情况中，柱塞与柱塞套的中心线很难完全重合，柱塞副环形间隙也不是理想的同心状态，由于忽略了柱塞侧向力及其倾斜，因此可认为此处柱塞副为偏心状态，如图3所示。

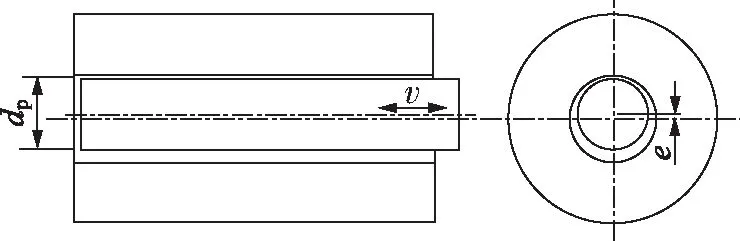
图3 柱塞副偶件相对位置示意图

在柱塞处于偏心状态时，柱塞副间隙泄漏量的计算公式为[12]：

(1)

式中,dp——柱塞直径,mm

h——柱塞副单边间隙,μm

μ——介质的动力黏度,Pa·s

l——柱塞副接触长度,mm

Δp——柱塞副间隙两侧压差,MPa

v——柱塞运动速度,mm/s

ε——偏心率，ε=e/h，e为偏心距(μm)

相较于柱塞同心下的柱塞副间隙泄漏流量公式，柱塞偏心下的计算公式增加了由柱塞偏心程度额外产生的泄漏量。式(1)右端第一项是由压差流引起的泄漏量，第二项是由剪切流引起的泄漏量。在实际情况中，柱塞吸行程与压行程相位相差180°，就剪切流来看，在一个完整的周期内由剪切流造成的柱塞副间隙泄漏可通过式(2)所示的积分进行计算：

(2)

式中，R0——缸孔分布圆半径,mm

ω——斜盘旋转角速度,rad/s

β——斜盘倾角,(°)

φ——当前位置的弧度值,rad

显然，无论柱塞的起始位置在何处，当柱塞运动完整的周期回到起始位置时，由剪切流引起的柱塞副间隙泄漏量可以相互抵消，即式q2值为0。因此可以认为，剪切流在完整的运动周期中对柱塞副间隙泄漏不产生影响。

2 仿真模型及参数设置

2.1 柱塞副间隙泄漏仿真模型

通过上述分析，本研究将主要针对压差流造成的柱塞副间隙泄漏量进行深入分析，在此基础上，用AMESim建立了图4所示的柱塞副间隙泄漏仿真计算模型。

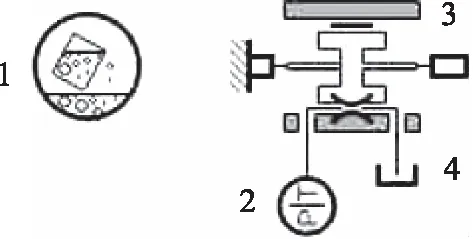
图4 柱塞副间隙泄漏仿真计算模型

仿真模型通过添加流体属性模块来模拟实际工作中的水介质，柱塞副间隙泄漏由热液压元件设计库中的泄漏模块模拟，柱塞副间隙两侧压差由热液压库中的理想压力源和油箱模拟。图4中所示的元件子模型选择如表1所示。

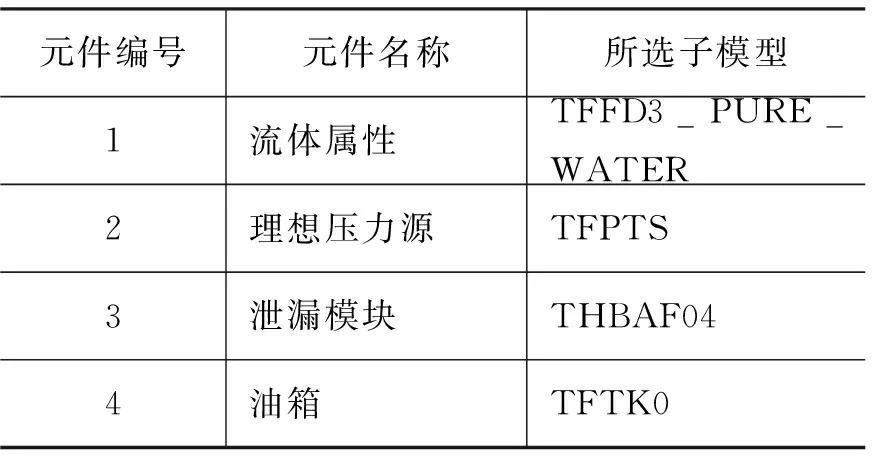
表1 元件子模型选择

流体属性模块通过空气分离压、饱和蒸汽压和完全汽化压力，将工作介质划分为4种状态[13]，即自由空气全部溶解进液体介质中、自由空气部分溶解进液体介质中、自由空气全部逸出且部分液体发生汽化、自由空气全部逸出且所有液体全部汽化。由于本研究中所涉及的压力最低为标准大气压，同时为了简化模型，忽略了混入水介质中的自由空气，使得工作介质仅为液相时的水介质。

2.2 水介质黏度变化

在柱塞副间隙内部流场中，随着沿轴向位置的不同，水介质的温度各不相同，因此需准确计算沿轴向不同位置处的水介质黏度。

如图5所示，在计算时沿柱塞轴向利用N个中间节点将柱塞副接触长度平均分为(N+1)份，通过每个区域的平均压力pi和平均温度Ti分别计算水介质黏度。水介质动力黏度的变化由压力和温度的多项式来计算，其式为[13]：

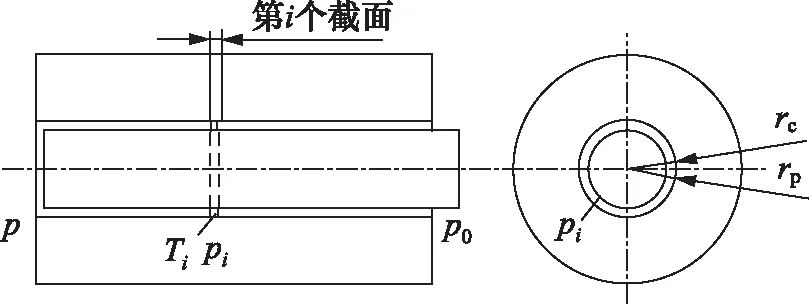
图5 柱塞副间隙流场划分示意图

μ=μ0·10λ

(3)

(4)

式中,μ0——初始状态动力黏度，Pa·s

λ——指数表达式

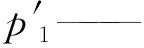
T0——初始状态温度，℃

Ti——第i个截面处平均温度，℃

p0——初始状态压力，MPa

pi——第i个截面处平均压力，MPa

在子模型为TFFD3_PURE_WATER的流体属性模块中，已包含了水介质的黏度变化，在实际计算中，仅需调用该子模型即可。

2.3 柱塞副间隙高压形变

柱塞副间隙大小沿轴向位置的不同而变化，其原因是在沿轴向不同位置处柱塞副间隙流场内部的压力不同，从而使得不同位置处的柱塞与柱塞套的变形不同，即柱塞副间隙大小由高压侧向低压侧递减。本研究忽略柱塞与柱塞套的轴向变形，仅考虑径向变形。在仿真计算时假设只发生弹性形变，遵循胡克定律，且柱塞副偶件材料的性能参数为恒定值，同时假设柱塞副偶件受到的内、外部压力均匀作用在柱塞副偶件的内、外表面上。

类似于黏度计算，柱塞副间隙高压形变也通过每个区域的平均压力pi分别计算变形量，本研究忽略高压对柱塞与柱塞套侧面的作用，仅考虑在柱塞副间隙流场压力下的径向变形。

本研究柱塞套外部受压为标准大气压p0，且柱塞套外径远大于柱塞套内径，得到第i个截面处柱塞套内径受压变形量为[14]：

(5)

式中,rc——柱塞套内半径,mm

Ec——柱塞套材料弹性模量,MPa

υc——柱塞套材料泊松比

针对柱塞，得到第i个截面处柱塞外径受压变形量为[14]：

(6)

式中,rp——柱塞半径,mm

Ep——柱塞材料弹性模量,MPa

υp——柱塞材料泊松比

结合式(5)和式(6)，便得到了第i区域柱塞副间隙总变形量的计算公式：

(7)

式(7)即为柱塞副间隙受压变形量的计算公式，在实际计算中，需将泄漏模块中间隙大小设置为“clearance by calculation”，再设置柱塞与柱塞套的弹性模量和泊松比，即可完成柱塞副间隙受压变形的相应计算。

2.4 仿真参数设置

仿真计算中，柱塞副间隙入口的工作压力变化范围为0～120 MPa，出口的压力始终为标准大气压，水介质的初始温度为20 ℃。本研究所涉及细长型柱塞的主要参数如表2所示，在仿真计算中通过修改泄漏模块的参数，以满足不同柱塞副单边间隙、柱塞副接触长度和柱塞偏心的要求。

表2 细长型柱塞主要参数

在仿真计算中，柱塞与柱塞套所选材料及材料属性如表3所示。

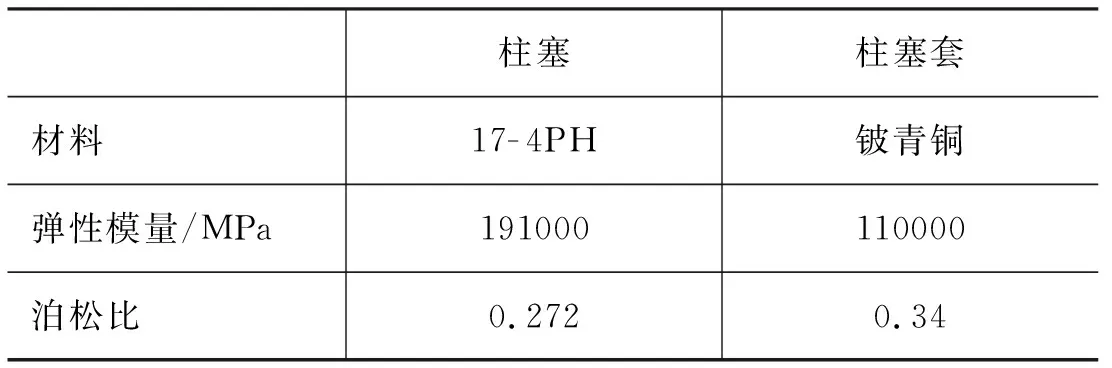
表3 柱塞与柱塞套材料属性

3 仿真结果分析

3.1 黏度变化和高压形变分别对间隙泄漏的影响

针对水介质黏度变化、柱塞副间隙高压形变对柱塞副间隙泄漏的影响进行仿真结果分析。计算时柱塞副单边间隙为5 μm，柱塞副接触长度为65 mm，本研究柱塞直径均为6 mm，称柱塞副间隙泄漏量占理论排量百分比为间隙泄漏占比U。理论排量均以电机转速1500 r/min、柱塞往复行程20 mm、柱塞直径6 mm时的单个柱塞排量来计算。

图6为水介质黏度变化对柱塞副间隙泄漏影响的仿真结果，柱塞处于同心状态下，仿真计算模型中设置间隙为5 μm。由图可以看出，水介质黏度变化使得间隙泄漏占比增加，在工作压力较低时，间隙泄漏占比变化幅度较小，当工作压力大于30 MPa时，其变化幅度开始增大，且随着工作压力的升高而增大的越快。究其原因是间隙泄漏的液压能损失转变为热能，使得间隙内水介质的温度及其黏度发生沿程变化。在这些产生的热量中，一少部分会不可避免地传递到柱塞和柱塞套上，但大部分用于使水介质的温度升高[15]，从而使自身黏度下降。由式(1)可知，水介质黏度下降会导致柱塞副间隙泄漏的增加， 在工作压力为30 MPa时， 水介质黏度变化使得柱塞副间隙泄漏占比增加了5.70%，在工作压力为120 MPa时增加了25%。显然在高压下由水介质黏度变化引起的间隙泄漏占比变化较大， 在计算时需要对水介质黏度变化加以考虑。在后续仿真计算中，均考虑了水介质黏度变化的影响。

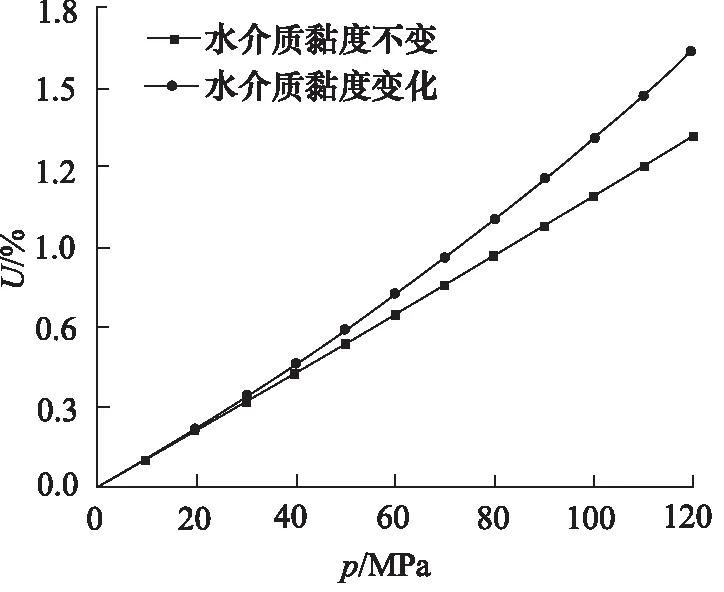
图6 水介质黏度变化对柱塞副间隙泄漏占比的影响

图7为高压形变对柱塞副间隙泄漏量影响的仿真结果，柱塞处于同心状态下，仿真计算模型中根据5 μm 的初始间隙计算变形后的间隙大小。由图可以看出，当柱塞副间隙不变时，随着工作压力的升高，间隙泄漏占比呈线性增长，当考虑柱塞副间隙高压形变时，间隙泄漏占比快速增长，且增长程度随压力的升高而越大。究其原因，当不考虑柱塞副间隙高压形变，即h为常数时，柱塞副间隙泄漏量与柱塞副间隙两侧压差Δp成正比关系，则显然有间隙泄漏占比随工作压力的升高而线性增长；当考虑柱塞副间隙高压形变时，柱塞副间隙大小在柱塞轴向沿程变化，随间隙内压力的升高而增大，而柱塞副间隙泄漏量与柱塞副单边间隙h的三次方成正比，因此间隙泄漏占比随着工作压力的升高而快速增长。在工作压力为120 MPa时，间隙高压形变使得间隙泄漏占比增加了3倍。显然由柱塞副间隙高压形变引起的间隙泄漏占比较大，尤其是在较高压力的情况下，因此计算时不能忽略柱塞副间隙高压形变。

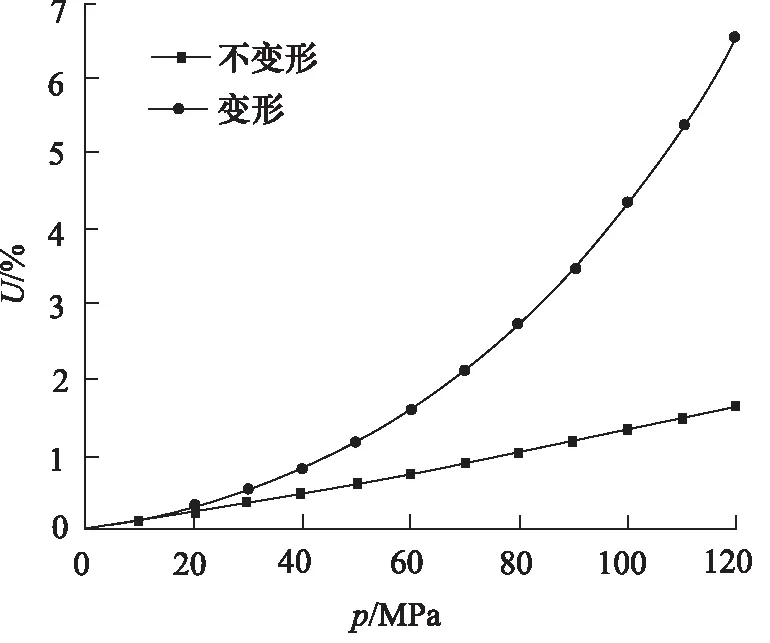
图7 高压形变对柱塞副间隙泄漏占比的影响

3.2 柱塞副结构参数对柱塞副间隙泄漏的影响

对柱塞偏心、柱塞副间隙大小和柱塞副接触长度对柱塞副间隙泄漏的影响进行仿真结果分析。

图8为不同柱塞偏心下的间隙泄漏占比。无论柱塞偏心程度是多少，随着工作压力的升高，间隙泄漏占比均呈线性增长，随着柱塞偏心程度的增加，间隙泄漏占比稳步增长，柱塞偏心100%时的间隙泄漏占比是柱塞同心时的249.99%，与理论计算的250%一致，因此在实际中不容忽略。在通常情况下，柱塞偏心程度为70%～80%。

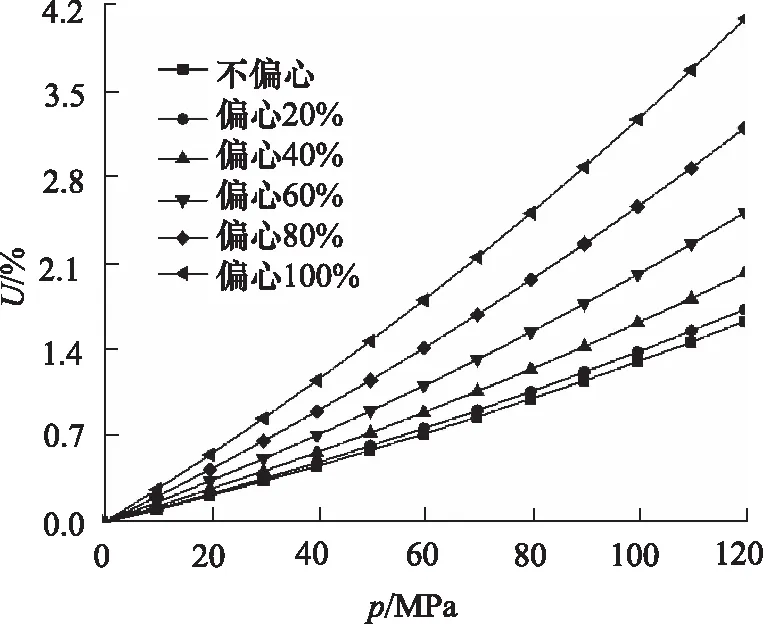
图8 不同柱塞偏心下的间隙泄漏占比

在后续计算中，均考虑了水介质黏度变化和柱塞副间隙高压形变，同时令柱塞偏心程度为80%。

图9为不同柱塞副间隙下的间隙泄漏占比，其中柱塞副接触长度65 mm。由图可以看出，随着柱塞副间隙的增加，间隙泄漏占比增大，当工作压力为120 MPa时，柱塞副初始单边间隙为3, 5, 7 μm时的间隙泄漏占比分别为3.51%,8.93%和18.51%。显然，在不同柱塞副间隙下间隙泄漏占比差异较大，7 μm 时的间隙泄漏占比是3 μm时的527.35%，因此减小柱塞副初始间隙，能够显著降低间隙泄漏占比，提高柱塞泵的容积效率。

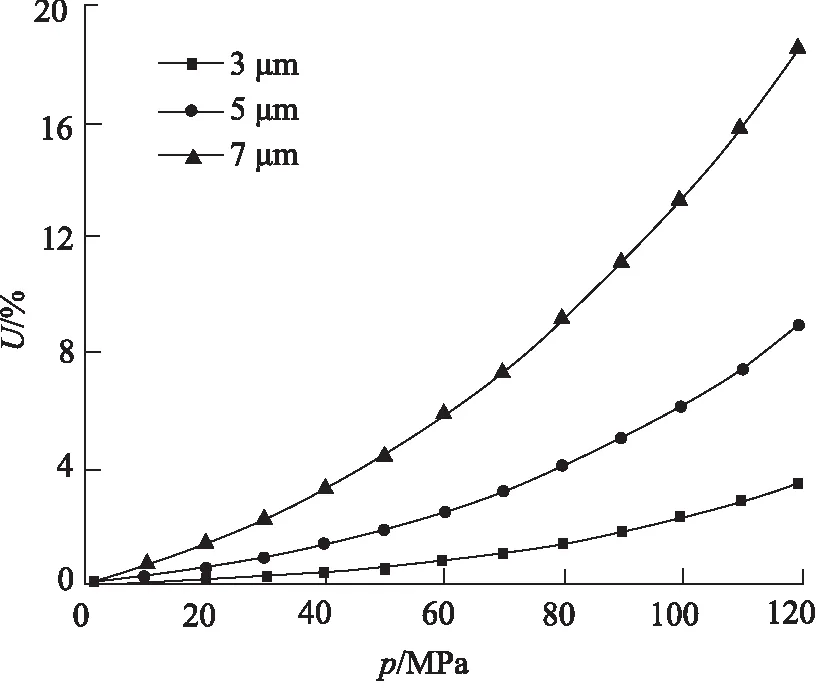
图9 不同柱塞副间隙下的间隙泄漏占比

图10为不同柱塞副接触长度下的间隙泄漏占比，其中柱塞副单边间隙5 μm。由图中可以看出，随着柱塞副接触长度的增加，间隙泄漏占比减小，当工作压力为120 MPa时，柱塞副接触长度为20, 35, 50, 65 mm时的间隙泄漏占比分别为29.01%，16.58%，11.60%和8.93%，显然由柱塞副接触长度引起的间隙泄漏占比变化较大。柱塞副接触长度为20 mm时的间隙泄漏占比是接触长度为65 mm时的324.86%，因此增加柱塞副接触长度是减小柱塞副间隙泄漏占比的有效途径；而柱塞副接触长度为50 mm时的间隙泄漏占比是接触长度为65 mm时的129.90%，由此可见，随着柱塞副接触长度的增加，柱塞副间隙泄漏占比在逐渐减小的同时，柱塞副间隙泄漏占比的减小速度在也在减小，即当柱塞副接触长度较短时，间隙泄漏占比的增长速度较快，而随着柱塞副接触长度的增加，间隙泄漏占比的增长速度在逐渐放缓。因此选取合适的柱塞副接触长度，能够在保证柱塞泵容积效率的情况下，尽可能使其结构紧凑。

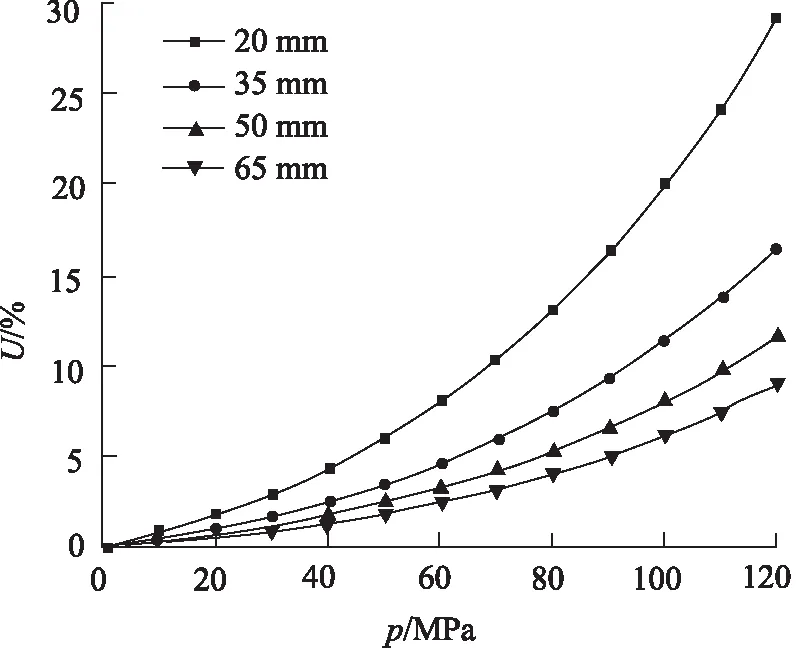
图10 不同柱塞副接触长度下的间隙泄漏占比

4 结论

(1) 随着工作压力的升高，柱塞间隙内水介质黏度沿程变化引起的泄漏量呈近似线性增长，在120 MPa时使得间隙泄漏占比增加了25%；间隙高压形变引起的泄漏量快速增长，在120 MPa时间隙泄漏增加3倍；

(2) 考虑间隙高压形变、黏度沿程变化，当配合间隙为3, 5, 7 μm时，间隙泄漏占比为3.51%，8.93%和18.51%；

(3) 超高压工况下，影响柱塞间隙泄漏的主要因素是柱塞副间隙大小、间隙高压变形量、柱塞副接触长度和柱塞偏心量；减小配合间隙大小、间隙高压变形量，增大柱塞副接触长度，可显著减小泄漏。