多策略改进的持续爆破算法
戴泽敏,曹连英
(东北林业大学 理学院,黑龙江 哈尔滨 150040)
0 引 言
持续爆破算法[1](continued explosion algorithm,CEA)是受炸弹爆破现象的启发而提出的一种新型智能优化算法。CEA算法具有原理简单、容易实现等优点,但是和其它大部分智能优化算法一样,CEA算法也存在容易陷入局部最优而导致早熟收敛的问题,此外,CEA在处理高维复杂优化问题时具有寻优能力差、寻优结果稳定性差等缺点。针对CEA存在的问题,本文提出一种基于主从结构的阶段寻优策略,并带有动态爆破半径和反向搜索变异的多策略改进的持续爆破算法(multi-strategy improved continued explosion algorithm,MSCEA),主要改进的工作体现在:①增加了初始炸点种群数量,由原来的单个炸点更改为多个炸点同时进行爆破寻优过程;②提出了一种基于主从结构的阶段寻优策略,并设计了动态爆破半径,有效提高了算法的局部寻优能力;③对算法中阶段最优解进行反向变异来代替适应度最差的阶段最差解,以此增加种群多样性,避免陷入局部最优;④通过位置更新策略令阶段局部最优解向阶段最优解的方向移动,提高了算法的收敛速度。
1 持续爆破算法
在持续爆破算法中,将炸弹(炸点)及其爆破产生的碎片(破坏点)所在的位置映射为目标函数的解。炸点爆破产生破坏点的过程相当于是对解的可行性空间进行的一次探索,若某一破坏点的适应度最优,则将此破坏点作为新炸点继续爆破寻优,若炸点的适应度最优,则扩大爆破半径继续生成新的破坏点。持续爆破算法通过更换炸点以及扩大炸点爆破半径等操作实现寻优过程。
定义目标函数f(x), 最大爆破代数Maxgen,代数叠加器gen,炸点x的范围(上界v,下界u),目标函数最优值M,半径扩大次数r,半径扩大次数上限Maxr,爆破半径Re,空间维度D,炸点爆破时产生的破坏点数量为q,每次爆破半径变化大小为Rchange(下文若出现相同符号,表示含义相同)。
持续爆破算法的具体实现步骤如下:
步骤1 在给定的D维解空间范围内随机生成一个初始炸点x。
步骤2 若满足gen Re=rand (1) 其中,rand为(0,1)范围内的随机数。 步骤3 随机生成q个爆破方向,并根据爆破半径生成q个破坏点,比较炸点和q个破坏点的适应度。若某一破坏点的适应度最优,则将此破坏点作为新炸点,执行步骤5;若炸点的适应度最优,说明没有找到优于炸点的破坏点,半径扩大次数r加1,执行步骤4。 步骤4 若满足r Re=Re+Rchange×r (2) x′=x+2×Re×I (3) 步骤5 代数叠加器gen加1,执行步骤2。 步骤6 当gen=Maxgen时,终止程序,同时输出当前适应度最优的值作为目标函数最优值。 持续爆破算法的不足可概括为4点:①初始炸点种群的多样性较低,对于多峰优化问题,单一炸点的爆破寻优过程容易导致算法陷入局部最优;②强制迁移炸点位置的变异方式容易使适应度较优的炸点丢失,导致算法的收敛能力较弱;③在CEA中,只有在未找到适应度优于炸点的破坏点时扩大半径搜索,没有实现爆破半径的动态变化,导致算法局部搜索能力较弱,搜索精度较低。 在“雇主/工人”[2]的主从式结构中,多个工人(子群)同时进行独立作业,并将信息反馈给雇主。雇主将信息整合分析,选取有用信息再传递给所有工人,以此提高工作效率,故本文将此结构融入CEA算法中。将CEA中单一炸点的爆破过程更改为n个炸点同时且独立完成imax次阶段寻优过程,其中每次阶段寻优过程都包括一次阶段局部寻优和一次阶段全局寻优过程。 第i次阶段全局寻优过程(雇主作业):将pbest(i)中适应度最优的解记为第i次阶段最优解gbesti,适应度最差的解记为第i次阶段最差解gworsti。 将imax次阶段寻优过程视为全局寻优过程,并将imax视为全局寻优迭代次数,将得到的gbestimax作为全局最优解。 在持续爆破算法中,炸点的爆破半径直接影响算法的寻优效率,半径过大会导致算法局部寻优能力差,寻优精度低,而半径过小又会导致算法跳出局部收敛的能力差。因此,针对每个炸点所进行的阶段局部寻优过程,设计了动态爆破半径。 当某一破坏点适应度优于炸点时,新的爆破半径公式如下 (4) 当炸点适应度优于破坏点时,新的爆破半径公式如下 (5) 此时p的值固定,搜索半径Re随着半径扩大次数r的增加而扩大,以此来继续寻找优于炸点的破坏点,实现了半径的动态变化,有效提高了算法的局部寻优能力。 反向学习策略被广泛应用于最优化问题[3-6],其中心思想在于在优化算法中,基于当前的最优解,同时评估其反向学习的解的适应度,择优进行选择。 定义1 若s=(s1,s2,…,sD) 为D维空间中的一个点,其中sh∈(uh,vh), 则根据式(6)定义s进行反向学习的解为s′ (6) 可以看出,根据反向学习策略生成的可行解相当于是对对称空间进行的一次搜索,有效扩大了搜索空间,增加了跳出局部最优的可能性,故本文将反向学习机制融入到CEA算法中。 在前期的阶段寻优过程中,通过式(7)和式(8)将gbesti进行反向变异后得到gbesti(*) 来代替gworsti gbesti(*)=u+v-gbesti (7) (8) 其中,iv表示全局寻优过程中的变异次数上限,如此既舍弃了表现较差的gworsti,也扩大了搜索空间,增强了算法跳出局部最优的能力。在后期的阶段寻优过程中,为提高收敛速度,不再进行反向搜索变异,以免算法收敛速度过慢影响寻优效率。 第i次阶段寻优结束之后,阶段局部最优解通过下述方式向阶段最优解的方向移动,产生第i+1次阶段寻优过程的初始炸点种群,以此实现种群之间信息的有效交互,平衡算法的局部搜索能力和全局搜索能力,提高了收敛速度和寻优效率。 (9) 图1描述了当i 图1 i 图2描述了当i≥iv时炸点的位置更新过程,依旧设二维搜索空间中第i次阶段寻优过程开始时有6个初始炸点,通过第i次阶段局部寻优过程得到了A-F这6个第i次阶段局部最优解,图2(b)表示找出A-F中适应度最优的B作为第i次阶段最优解,图2(c)表示A、C-F分别通过式(9) 向B移动得到A’、C’-F’。最后,将A’、C’-F’、B作为第i+1次阶段寻优过程开始时的6个初始炸点。 图2 i≥iv时炸点的位置更新 步骤1 初始化各个参数,随机生成n个炸点作为第1次阶段寻优过程的初始炸点种群pop1。 步骤2 若满足i≤imax,则令p=1,n个炸点独立进行阶段局部寻优过程,分别执行步骤3~步骤8;否则转至步骤12。 步骤3 若满足p≤Maxp,则令r=1,根据式(4)生成爆破半径Re;否则转至步骤8。 步骤4 随机生成q个爆破方向,并根据爆破半径生成q个破坏点。 步骤5 根据目标函数计算并比较炸点和q个破坏点处的适应度,若某一破坏点的适应度最优,则将此破坏点作为新炸点并转至步骤7;若炸点的适应度最优,说明没有找到优于炸点的破坏点,执行步骤6。 步骤6 若满足r≤Maxr,则根据式(5)扩大爆破半径,r=r+1,转至步骤4;否则执行步骤7。 步骤7p=p+1,返回步骤3。 步骤9 当n个炸点全部完成步骤3~步骤8时,会得到一个阶段局部最优解集pbest(i)、阶段最优解gbesti和阶段最差解gworsti。 步骤10 判断是否满足i 步骤11i=i+1,转至步骤2。 步骤12 输出当前阶段最优解作为全局最优解。 本文仿真实验环境:64位Windows 10操作系统,处理器为Intel(R) Xeon(R) Gold 6242R CPU @3.10 GHz 3.09 GHz(2处理器),内存为256 GB,编程软件为MATLAB R2019b。 为了验证算法的可行性和优越性,本文采用表1中的函数作为测试函数,既包括检验算法寻优精度的单峰函数,也有检验算法避免早熟收敛、跳出局部最优能力的多峰函数。 表1 测试函数 本文算法的基本参数设置如下:每次阶段寻优的初始炸点种群数量n=10,每个炸点单次爆破生成的破坏点数量q=5,函数f1~f7的维数D=30,全局寻优迭代次数imax=1000。 以较难寻得最优解的f4~f6函数为例,表2给出了随着Maxp、Maxr和iv的变化,函数f4~f6的部分寻优结果。由于iv是全局寻优过程中的变异次数上限,变异次数过少会造成算法跳出局部最优的能力不足,容易导致早熟收敛,而次数过多会导致算法后期收敛速度缓慢,降低寻优效率,所以设置全局寻优迭代次数imax的30%、60%、90%,即300、600、900作为iv的取值进行仿真实验,取10次实验结果的平均值与标准差。经过多次实验并且综合考虑所有测试函数的寻优效果,将迭代参数设置如下:Maxp=400,Maxr=10,iv=imax×90%。 表2 Maxp、Maxr、iv不同取值下的实验结果对比 3.4.1 与CEA对比 为充分说明MSCEA的可行性与有效性,在表3中将其与原始持续爆破算法(CEA)进行比较。CEA算法参数设置:将Maxgen视为全局寻优迭代次数,同样取Maxgen=1000,其它参数设置与原文献保持一致。因为CEA中的初始炸点和MSCEA中第一次阶段寻优的初始炸点种群pop1均为随机生成,为了降低算法结果的偶然性,对每个测试函数都独立进行20次仿真实验后记录平均值和标准差,并将算法中最好的寻优结果加粗表示。 表3 CEA与MSCEA的实验结果对比 通过表3可以看出,对于函数f8,CEA和MSCEA均能寻得最优值,说明MSCEA和CEA均具备寻找到不为0的最优值的能力;对于其它测试函数,多策略改进后的持续爆破算法的寻优结果均优于持续爆破算法。相比于CEA,MSCEA的寻优精度大幅度提高,除函数f2外,均能找到测试函数的理论最优值。虽然MSCEA无法找到函数f2的理论最优值,但是与CEA算法相比,寻优精度提高了16个数量级。对于最优解不在原点的f8、f11和f12函数,MSCEA也能找到理论最优值,说明MSCEA不存在易在原点或原点附近寻优的缺陷。同时从表3中的标准差可知,MSCEA算法在函数f1~f12上得到的标准差都为0,说明MSCEA算法具有较强的鲁棒性。综合分析说明MSCEA算法具有较强的搜索能力,表现出良好的寻优性能。 为对种群多样性进行分析,图3展示了f1函数在D=3,n=100时不同次阶段寻优时初始炸点的分布情况,其中popi表示第i次阶段寻优过程的初始炸点种群,因为维数较低,炸点能很快靠近理论最优解,验证了MSCEA算法的可行性。通过图4给出的初始炸点种群pop20和pop70的局部放大图可以看出,随着阶段寻优次数的增加,炸点在寻优精度越来越高的同时仍然在一定范围内保持着较高的种群多样性,说明由阶段局部最优解向阶段最优解移动的种群更新策略能够对可行解空间进行更加细致的搜索,有效平衡了算法的局部开发和全局勘探能力,提高了算法的寻优精度。 图3 炸点分布 图4 局部放大图 为更直接地了解改进算法的收敛速度和探究反向搜索变异策略对寻优效果的影响,图5给出了CEA、MSCEA-1、MSCEA在测试函数上的迭代收敛曲线图,其中MSCEA-1算法为MSCEA算法去掉对阶段最优解的反向变异操作。为方便观察,对得到的适应度值取以10为底的对数。从图5可以看出,对于函数f1、f7~f12,MSCEA-1和MSCEA的收敛曲线基本重合,收敛速度和寻优精度相比于CEA均大幅度提高,这表明反向变异策略对这些函数寻优结果的影响较小,说明主从结构的阶段寻优策略的有效性,平衡了算法的局部开发和全局勘探能力,动态寻优半径能大幅度提高寻优精度。而对于函数f3~f5,CEA和MSCEA-1在迭代前期均会陷入局部最优,表明反向搜索变异策略扩大了搜索空间,能够有效加强算法跳出局部最优的能力。对于函数f2和f6,MSCEA-1和MSCEA的寻优精度明显提高,也能快速达到收敛状态,并且从图中可以看出,加入反向变异策略的MSCEA算法寻优精度更高,收敛速度更快,说明反向变异策略能够避免早熟收敛。 图5 测试函数的收敛曲线 3.4.2 与其它算法对比 为进一步体现MSCEA算法的寻优性能,将其与混合策略改进的麻雀搜索算法(MSSSA)[7]、基于翻筋斗觅食策略的灰狼优化算法(DSF-GWO)[8]、一种用于全局优化的增强型鲸鱼优化算法(EWOA)[9]、一种改进的量子粒子群优化算法(e-QPSO)[10]、基于自适应策略的萤火虫算法(SAFA)[11]、一种改进的布谷鸟搜索算法(NMS-CS)[12]进行比较。由于不同类型优化算法的机制不同,所以本文直接引用了参考文献[7-12]中所给出的相同维数下的数据结果进行比较,并将算法中最好的寻优结果加粗表示,MSCEA算法的实验参数设置与3.3节一致,数据对比见表4。 表4 相同维度下的不同算法的寻优结果对比 表4(续) 根据表4中给出的数据可以直观地看出不同算法对于函数的寻优效果不同,只有MSCEA能找到函数f5的最优值,说明MSCEA有能力避免早熟收敛,有效解决函数优化问题。此外,只有MSCEA在6个函数上的寻优结果均为最优,说明MSCEA具有较为出色的寻优表现,在优化算法中具有较强的竞争力。 为验证MSCEA在高维下的寻优性能,表5给出了CEA和MSCEA在高维(50、100维)函数优化中的平均值和标准差,算法的实验参数设置与3.3节和3.4.1节一致。从表5可以看出,在高维情况下,MSCEA算法仍能寻得部分函数的理论最优值。对于其余部分函数,MSCEA算法虽然没能找到理论最优值,但寻优精度相比于CEA均大幅度提高。 表5 高维下的实验结果对比 此外,继续增加全局寻优迭代次数至4000次,即CEA中Maxgen=4000、MSCEA中imax=4000,其余参数设置与3.3节和3.4.1节一致,实验结果见表6。从表6可以看出,CEA的寻优精度虽然有所提高,但依旧未能得到f1~f7函数的最优值。而MSCEA对除f2外的函数均能找到最优值,对于f2,寻优精度也相比于CEA提升了17个数量级左右。 表6 增加全局寻优迭代次数后的实验结果对比 综上,在30、50、100维条件下,随着维数的增加,MSCEA整体上都能表现出较好的寻优效果。MSCEA不仅寻优精度高,而且鲁棒性强,大部分测试函数的寻优标准差不随着维数的增加而增加,说明MSCEA寻优性能优越,在处理高维优化问题方面具有一定的竞争优势。 本文针对持续爆破算法易陷入局部最优、寻优精度较低等缺点,提出一种基于主从结构的阶段寻优策略、并带有动态爆破半径和反向搜索变异的多策略改进的持续爆破算法。通过进行MSCEA与CEA、MSCEA-1在低维下的实验数据对比,说明主从结构的阶段寻优策略能有效平衡算法的局部寻优和全局寻优能力,引入的反向变异搜索策略可以提高算法跳出局部最优的能力。将MSCEA与鲸鱼优化算法、灰狼优化算法、萤火虫算法等多种优化算法的近期研究成果进行比较,表明MSCEA能有效避免早熟收敛,提高算法精度,在优化问题上具有较强的竞争优势。通过高维下的寻优性能测试,说明MSCEA寻优精度高、寻优性能稳定,可以有效处理高维优化问题。此外,针对部分函数的高维优化问题,如何能通过更少的全局寻优迭代次数达到和低维时相同的寻优精度和收敛速度,以及如何将MSCEA应用于实际优化问题,是今后需要研究改进的方向。2 改进的持续爆破算法
2.1 持续爆破算法(CEA)存在的问题
2.2 基于主从结构的阶段寻优策略
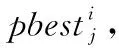
2.3 自适应动态爆破半径
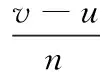
2.4 阶段最优解的反向搜索变异
2.5 每次阶段寻优初始炸点的位置更新策略
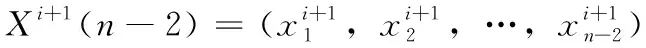
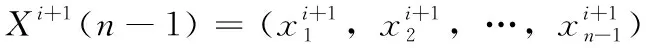



2.6 具体步骤如下

3 仿真实验与结果分析
3.1 仿真实验环境
3.2 测试函数

3.3 参数设置
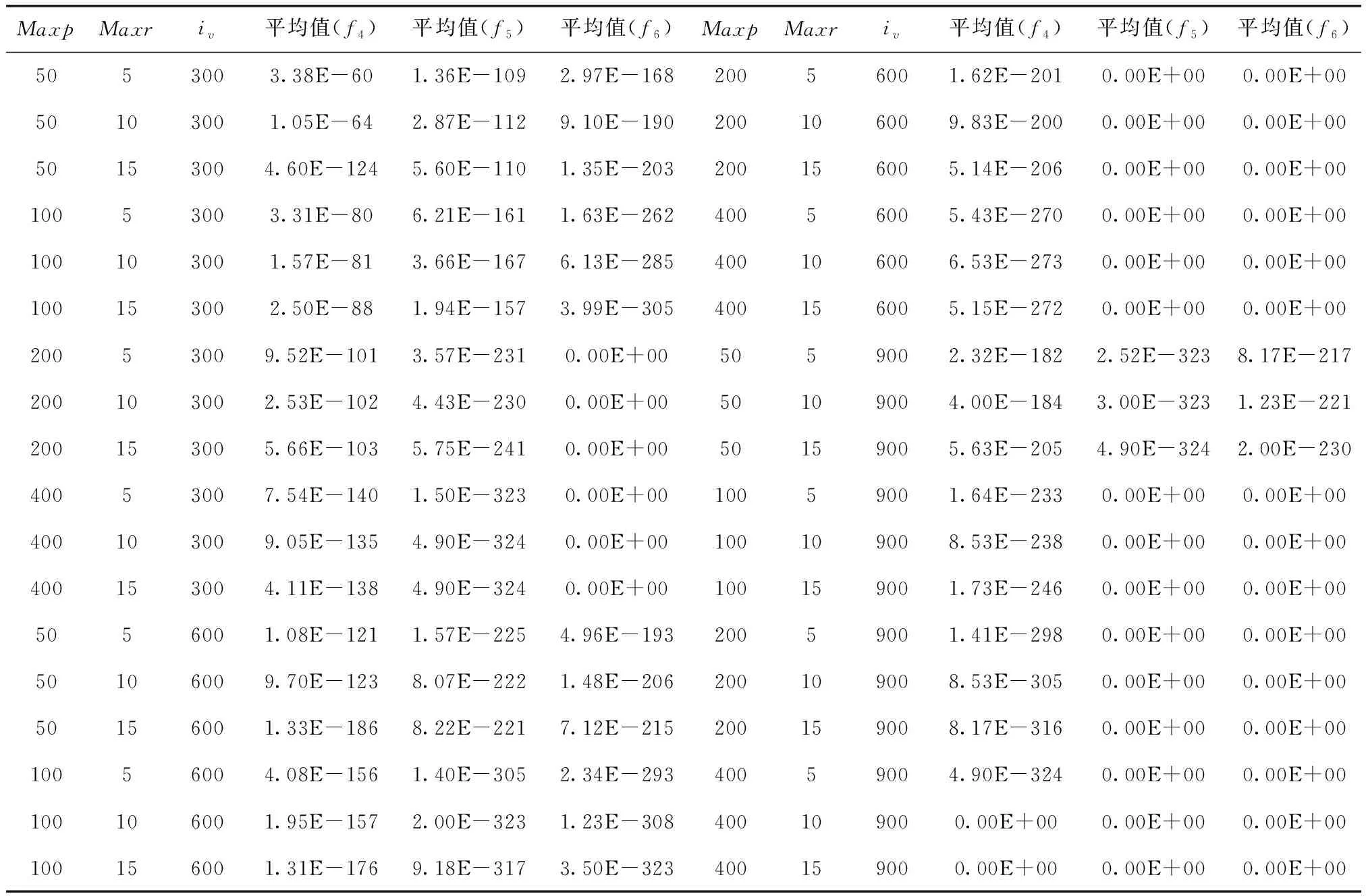
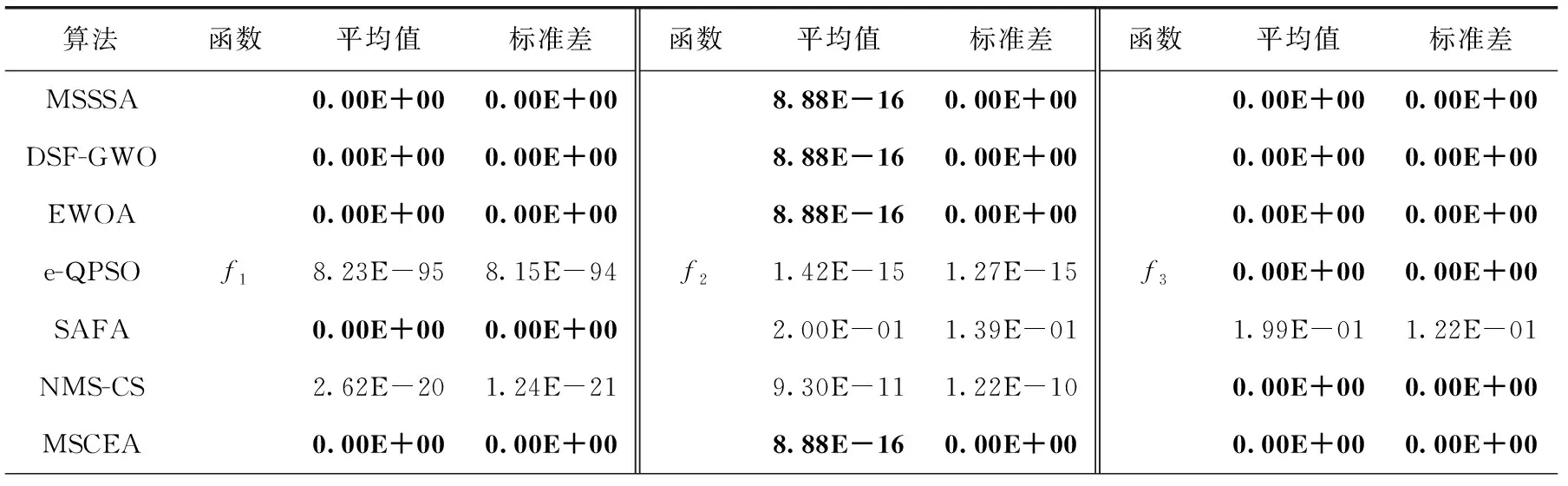
3.4 实验结果及分析

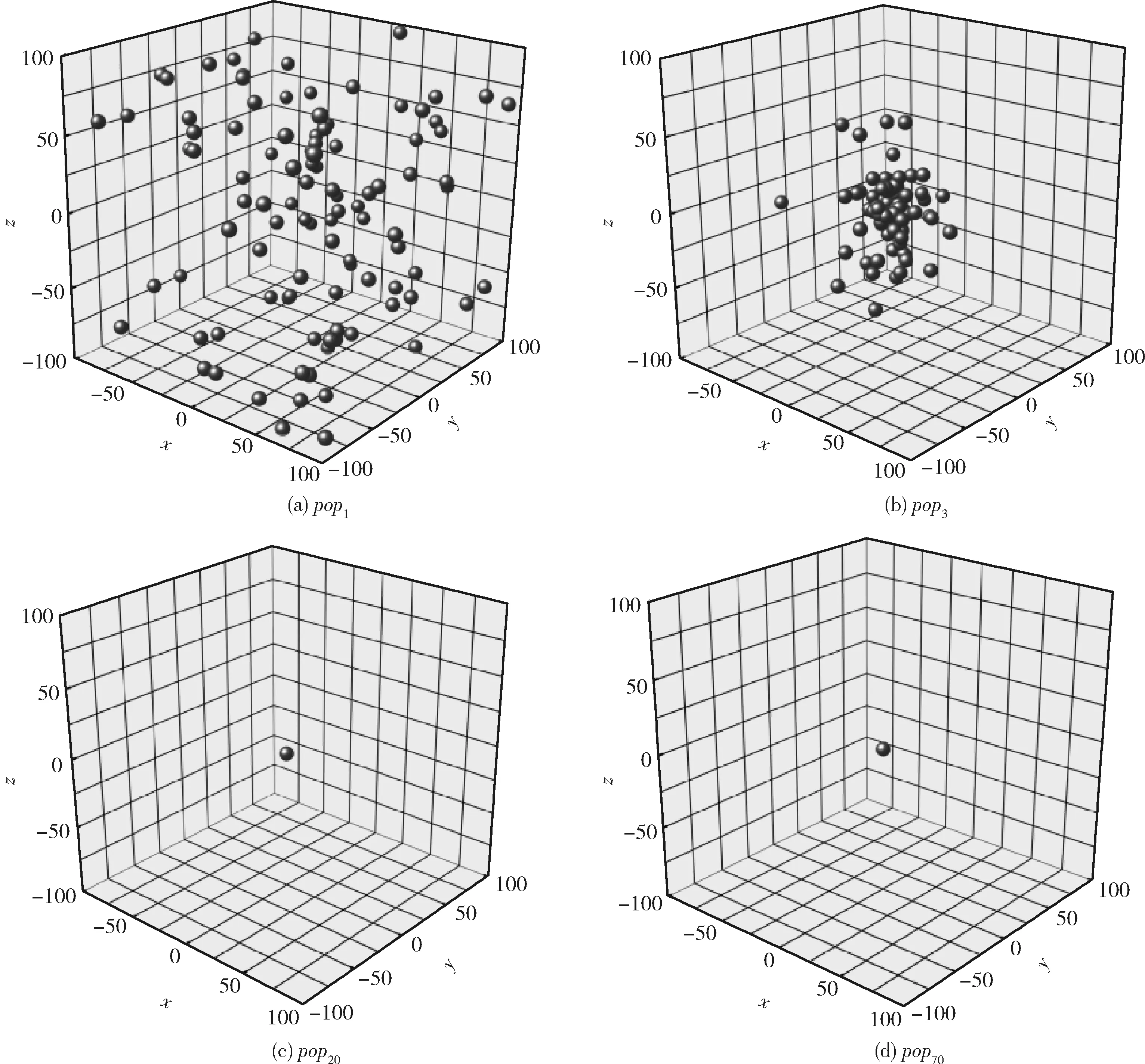
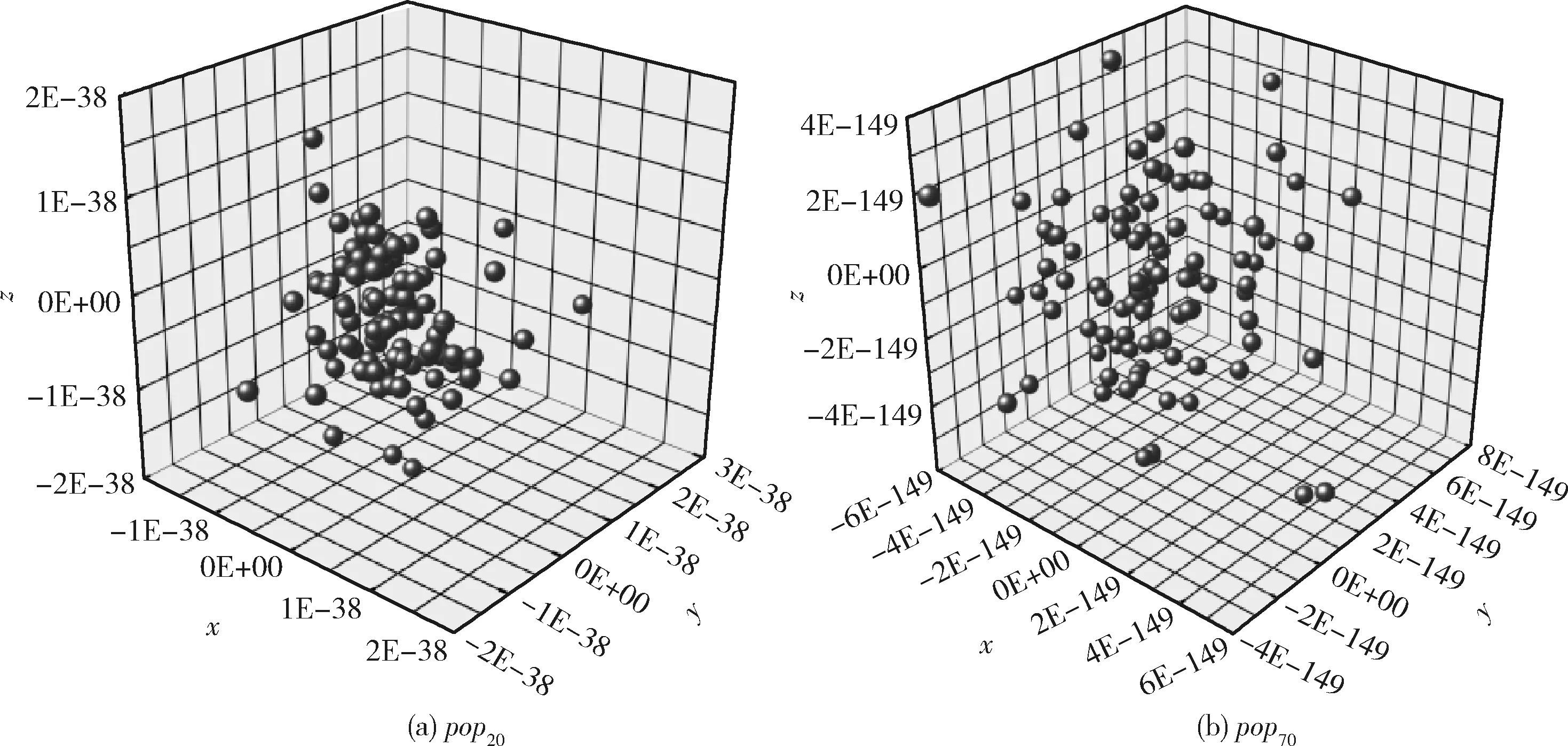
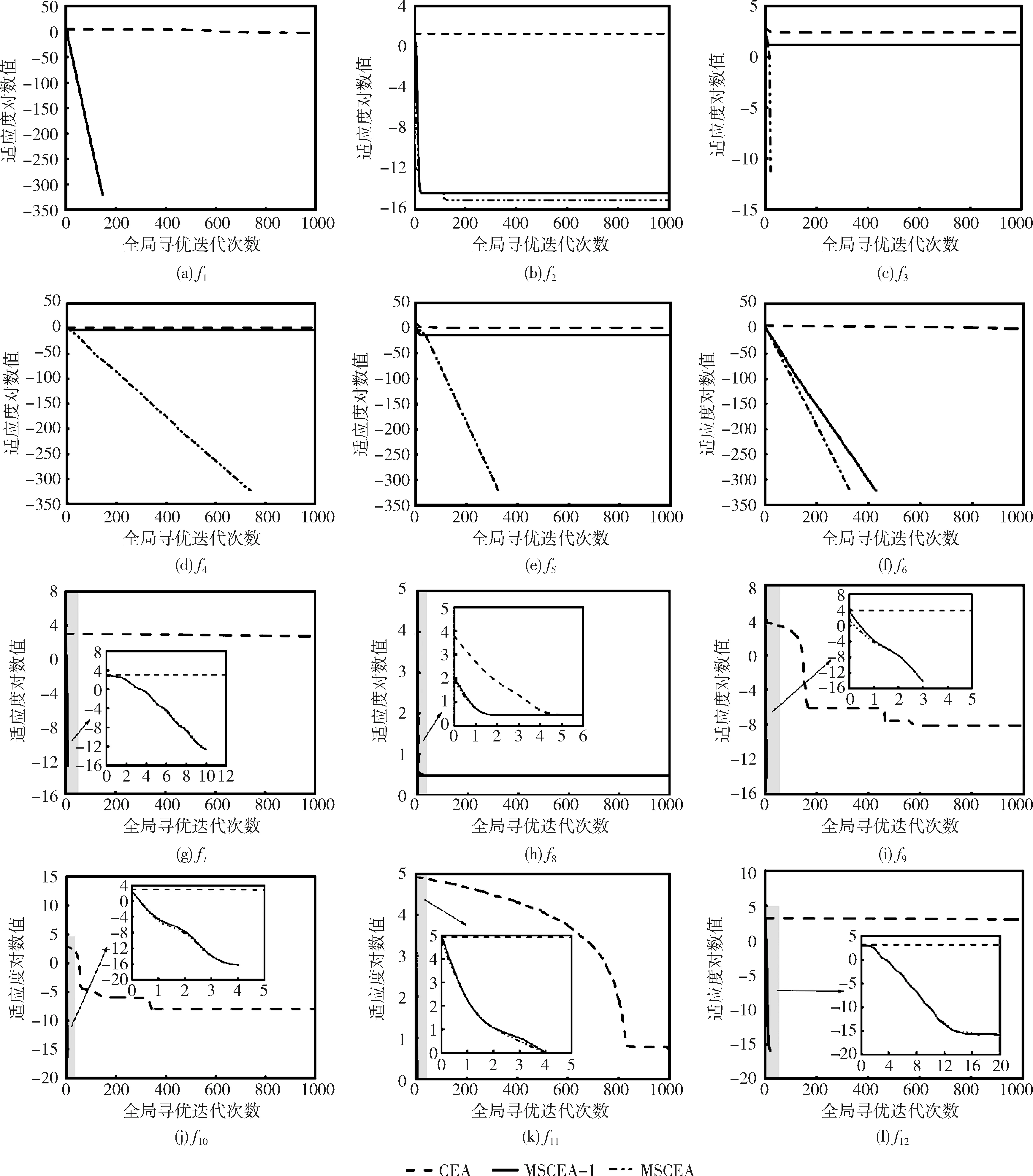

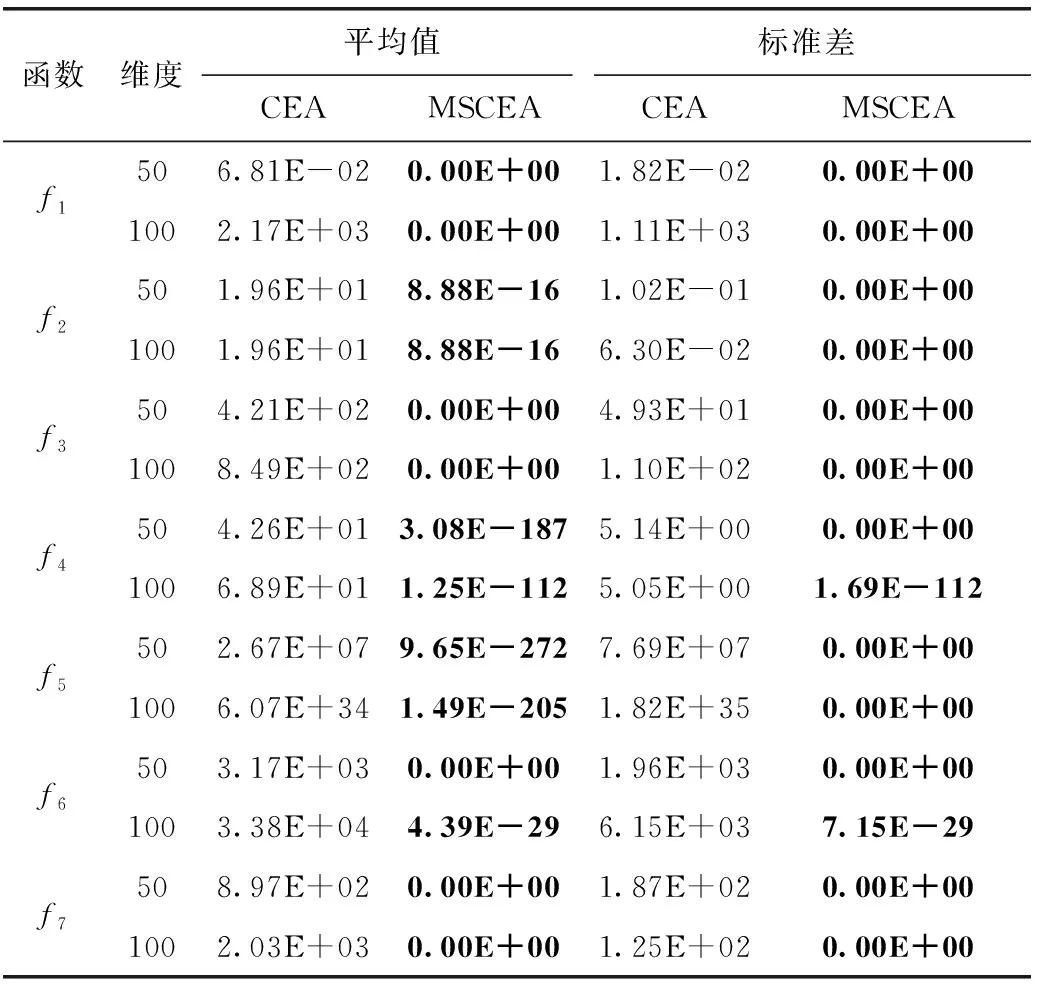
3.5 高维下的性能测试

4 结束语

