基于门限签名的分布式预言机链下共识方案
孙 舟,祝秀山,刘祥路,陈 振,袁小溪
(国网北京市电力公司 电力科学研究院,北京 100075)
0 引 言
随着智能电网建设的不断推进和区块链技术的快速发展,利用区块链实现海量电力数据的安全存储成为电力数据管理的主要趋势[1]。而在实际应用过程中,为了实现链下可信数据的实时安全上链,通常借助预言机来保障数据传输和处理过程的安全可信。2015年,中心化预言机Oraclize(现更名为Provable)被首次提出,依托亚马逊云主机、Google等可信第三方来证明数据的真实性[2]。2017年,第一个基于以太坊的去中心化预言机网络Chainlink被提出,通过多数据源和多预言机节点的方式有效分散了因数据来源本身的问题导致数据失真的风险,并引入声誉系统和验证系统[3]。2019年,去中心化预言机DOS Network白皮书正式发布,利用可验证随机方程和阈值密码学来保证可验证工作节点的随机选取[4]。
相较于中心化预言机基于可信第三方的证明机制,去中心化预言机网络通过多个预言机节点之间相互验证的模式能够更好地保障上链数据的可信性。然而,现有的分布式预言机网络通常采用链上共识的方式,即每台预言机都需要将响应发送至区块链上的智能合约,由聚合智能合约进行数据共识得到单一数据点。但是由于每个预言机节点都要将外部数据上传到区块链,容易造成区块链网络压力大、共识效率低等问题。为此,本文提出一种基于门限签名的分布式预言机链下共识方案,通过设计各预言机节点链下签名、共识并上链的过程,在保证数据共识过程安全可靠的同时,减缓区块链网络压力,提高共识效率。
1 关键技术
1.1 预言机
区块链是一个点对点的分布式账本系统[5],而智能合约是无需中介、自我验证、自动执行合约条款的计算机交易协议[6],区块链与智能合约的结合,有利于切实解决电力、农业、经济、医疗等领域的部分难题。但是由于区块链具有特殊的底层共识协议,链上智能合约只能在一个封闭、孤立的环境中执行任务,无法与外部系统交互[7]。针对这一问题,预言机技术提供了一种让智能合约可以请求外部数据的途径。
在区块链环境中,预言机是一个外部数据代理,它观察区块链外部世界的事件,并将其报告给区块链,供智能合约使用,从而扩大了区块链和智能合约的应用场景[8]。目前,预言机可分为中心化预言机和去中心化预言机。文献[9]提出了中心化预言机方案Town crier,它会正确地执行代码,有效将外部数据输入到区块链,但是依赖单一预言机节点容易遭遇单点故障、数据滥用、中心化信任等问题,导致区块链上出现恶意或错误的数据;文献[10]进一步提出了去中心化预言机方案,由多个预言机节点同时获取数据,有效解决了中心化预言机带来的问题,同时能降低被虚假信息干扰的风险,提供了更好的安全保障。如今,通过预言机搭建实现区块链与链外世界统一融合的平台已逐渐成为一种趋势[11]。
1.2 预言机共识机制
共识机制指网络中所有节点通过事先确定的规则对某个提案形成共同认识的过程[12]。对于中心化预言机,外部信息直接被获取到区块链中。对于分布式预言机,多预言机节点中可能存在问题预言机,这将导致数据不一致问题,因此所有预言机需要通过一种特定规则对最终提交给区块链的数据达成一致,即所有预言机返回的数据需要以可信的方式被聚合成一个单一且权威的数据。例如,在区块链平台Augur和Gnosis中,多个预言机节点使用投票的方式来达成对要接受的答案的共识。
现有的去中心化预言机网络通常采用链上共识的方式,每台预言机都需要将响应发送至链上智能合约,由这个智能合约负责数据共识,这样可以有效防止部分节点提交错误数据而对结果造成影响,保证数据的真实可靠,同时整个执行过程在链上完全公开透明,可信度高[13]。但是这种合约内聚合的方法要求每个预言机节点都将外部数据上传到区块链,容易造成区块链网络压力增大,运行效率降低。而门限签名技术作为一种分布式多方签名协议,可以带来多种区块链场景下的效率提升。文献[14]提出门限签名方案可以有效降低计算资源需求量,提升签名生成阶段的效率。门限签名技术也可以应用于分布式预言机共识算法中,降低通信复杂度,保障共识过程的客观准确性和上链数据的可信性。
2 分布式预言机链下共识方案
为了解决现有的分布式预言机网络链上共识存在的区块链网络压力大、共识效率低等问题,提升链上性能,本文提出一种基于门限签名的分布式预言机链下共识方案,让预言机在链下交流并达成共识,然后经由统一的预言机一次性发送至区块链上的智能合约,而不需要每个预言机节点都将响应发送至区块链上的智能合约,减少了造成区块链网络拥堵的可能性,减缓了区块链网络压力,提高了共识效率,从而实现时变数据实时与高效共享。
2.1 智能合约设计
为了实现预言机池与区块链和外部数据源之间的数据交互,我们设计了以下两个智能合约。
(1)数据请求智能合约:用户用于向外部数据源请求数据的智能合约,负责接收用户的数据访问请求并调用预言机智能合约;
(2)预言机智能合约:作为数据请求智能合约和预言机之间的中介,负责向预言机池发送数据请求、接收返回的电力数据和签名以及计算和管理每个预言机节点的信誉。
图1展示了来自用户的数据请求是如何传递到外部数据源以及外部电力数据是如何被传输返回给用户的。想要获取外部电力数据的用户需要创建一个数据请求智能合约(1),通过数据请求智能合约调用预言机智能合约(2)。然后,预言机智能合约会为每个请求分配唯一的事件ID,并生成一个区块作为事件日志记录事件ID、请求信息和接收请求的预言机节点列表(3),并对请求信息进行签名后发送给预言机池中的预言机节点(4)。各预言机节点对请求进行验证后,从外部数据源获取对应的电力数据(5)。

图1 数据请求和外部电力数据的传输过程
而在数据传输过程中,首先每个预言机节点对获取到的外部电力数据进行签名,然后发送给参与请求的其它预言机节点(6),各节点对接收到的签名进行认证并进行数据共识,聚合成单一数据后(7),由聚合预言机将数据和签名信息发送给预言机智能合约(8)。最后,预言机智能合约对接收到的数据和签名进行验证后通过回调函数将数据返回给数据请求智能合约(9)。
2.2 分布式预言机链下共识方案设计
2.2.1 方案描述
我们通过(t,n)门限签名技术来实现分布式预言机网络的链下共识。(t,n)门限签名技术是指在一个由n个参与者构成的签名群体中,有一个公私钥对,通过一定的方式将这个私钥切分成许多碎片,并分发给群体中的所有参与方。当群体中任意数量大于等于t个参与者使用各自的私钥碎片对同一个数据进行签名时,就可以产生一个完整的有效签名。其中t为门限值,也是就生成合法签名的最小参与者数量,当签名方的数量小于t时,则无法生成有效签名。
通过门限签名技术,分布式预言机网络中的n个预言机节点在链下进行交互,当t个预言机节点针对同一个值分别生成部分签名时,就可以聚合成一个完整的密钥签名,并可以批准数据传输,将共识后的数据发送至区块链上的预言机智能合约,因此,最后只需将一条经过验证的信息传输至链上进行处理即可,无须将n条预言机信息都发到链上。虽然只有网络中参与的预言机才能组成签名,但是任何人都可以检查签名的真实性和有效性。相较于传统链上共识方案中预言机智能合约需要对针对同一个数据生成的t个签名进行验证,通过门限签名的分布式预言机链下共识方案在安全性上无异,但是预言机智能合约只需要对最终合成的一个完整签名σ进行验证,从而将验证签名σ的计算工作量和成本降低了t倍,使得链上性能大幅提升。
2.2.2 提交-揭露机制
此外,分布式预言机的链下共识方案需要解决预言机的“吃空饷”问题,即预言机节点不是通过访问数据源来获取数据,而是抄袭其它预言机的答案。吃空饷现象会削弱数据源的多样性,也会打击预言机快速响应的积极性,因为响应速度慢的预言机可以免费复制别人的答案。当大量吃空饷的节点复制了一个错误答案时,将造成大多数攻击,影响系统安全性。
为了解决这一问题,我们采用了提交-揭露机制,即预言机节点分两个阶段提交数据,在第一阶段,预言机将数据以加密的形式进行提交,并收集其它预言机提交的密文信息,只有在收到合法数量的密文信息后,才会开启第二阶段,对所有结果进行解密用以验证数据。只有进入取消提交阶段,所有数据结果才会公开,从而避免了预言机的抄袭问题。
2.3 分布式预言机链下共识方案算法
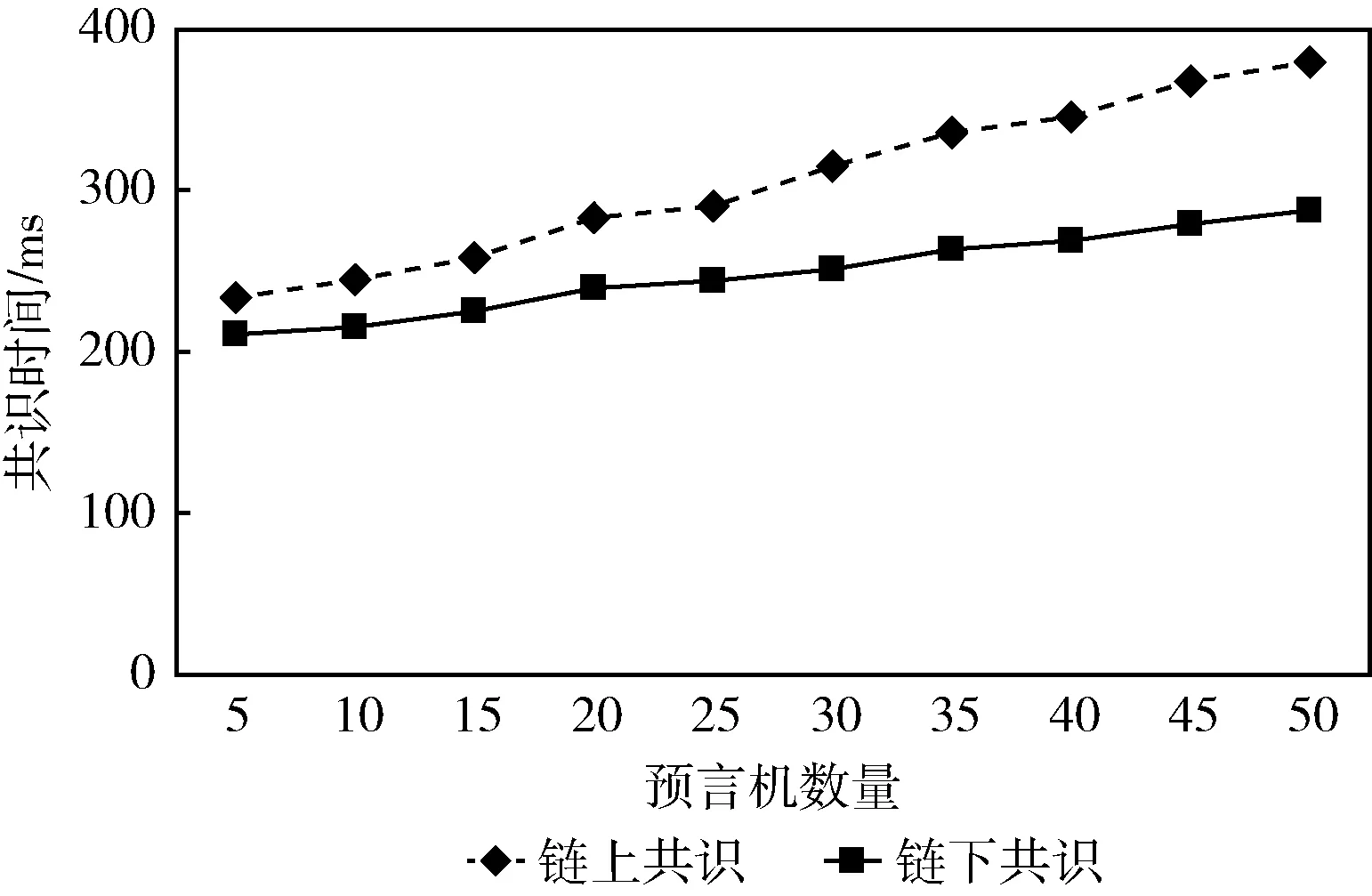
在本方案中,我们假设有f 图2 分布式预言机链下共识方案流程 假设参与共识的预言机节点集为O={O1,O2,…,On}, 共n个预言机节点,门限值为t。选定安全参数k,选择一个q阶循环群G,其离散对数问题是难解的,有限域q元素个数为q,特征值为p,p、q为大素数,g是G的生成元,选择安全哈希函数H1公开参数为k、p、q、g、G、H1和H2。此外,我们用表示从S中选取随机数x。 2.3.1 密钥生成 构造分布式密钥生成(distributed key generation,DKG)协议,将O的密钥n等分分发给所有预言机节点Oi,使得数量≥t的任意个预言机节点集合都可以针对同一个值合成完整的数字签名,而t-1台预言机的集合则无法对任何值生成合法签名,从而保证这个完整签名至少由t台预言机的部分签名组成。 在本方案中,我们基于Pedersen DKG协议进行密钥生成,不需要可信中心的参与,而是在通过分布式协作下生成密钥,避免单点泄漏风险,相当于n个节点同时各自选择秘密值并运行自己的可验证秘密分享,每个节点收集来自其它节点的秘密份额完成组装,组装后的结果便是真正密钥份额。 除了基本的Pedersen DKG协议外,我们还要求每个参与的预言机节点通过零知识证明(例如Schnorr签名)来证明他们知道秘密值ai0,以防止在t≥n/2时的欺骗攻击。协议运行输出一个全局公钥Y和每个预言机节点Oi各自所有的密钥份额si和公钥份额Yi。在后续的签名阶段,参与共识的预言机节点可以通过每个节点的公钥份额Yi对该节点的签名份额进行验证;而在签名验证阶段,除参与共识的预言机节点集合外的实体则可以通过全局公钥Y对该集合得到的完整签名进行验证。具体的分布式密钥生成协议如下: (1)第一轮 1)每个预言机节点Oi选择t个随机数 以这些随机数为系数构建t-1阶多项式 2)Oi对相应的秘密值ai0计算知识证明 σi=(Ri,ui) 3)Oi计算公开承诺 其中,φij=gaij, 0≤j≤t-1。 其中,cl=H(l,Φ,φl0,Rl)。 (2)第二轮 1)Oi向其它预言机节点Ol发送密钥份额 (l,fi(l)), 在保存 (i,fi(i)) 后,删除fi和其它密钥份额。 2)Oi收到其它节点发送的 (i,fl(i)) 后,验证等式 若验证失败则终止协议。 3)Oi计算自己的密钥份额 保存si,然后删除所有fl(i)。 4)Oi计算公钥份额 Yi=gsi 全局公钥 任何节点可以通过以下等式计算其它节点的公钥份额 2.3.2 签名生成 各预言机节点通过自己的密钥份额si对数据结果进行分布式协作签署,生成部分签名σi,可以用Yi进行验证,然后通过聚合输出最终的可验证完整签名σ,这个签名和单独用全局密钥s签出的签名是一样的,可以用全局公钥Y进行验证。每个预言机节点进行签名的具体实施步骤如算法1所示。 算法1:签名生成协议 获取数据: (1)从外部数据源获取数据Di 生成部分签名: (2)计算得到部分签名σi=Sigsi(Di) 结果提交轮: (3)广播提交的结果commi=Commit(σi,Di), Commit为提交函数 (4)等待收到n-f个来自不同预言机的合法提交集合Ci (5)将Ci发送至预言机智能合约 准备轮: (6)广播prepared信息 (7)等待收到n-f条不同预言机的prepared信息解密/取消提交轮: (8)广播 “取消提交commi”的信息 (9)等待收到一组≥t的合法取消提交的信息PS 计算完整签名: (10)合成完整数字签名σ=Sigs(D), 其中D=Agg(D1,D2,…,Dn), Agg为多数函数 (11)将PS发送至预言机智能合约 签名生成阶段的具体实现与所基于的数字签名算法有很大关系,常用的算法包括ECDSA签名算法和Schnorr签名算法。在本方案中,我们采用Schnorr签名算法来生成完整的合法签名,同时利用了绑定技术,在不限制并发性的情况下防止伪造攻击。我们将签名过程分为预处理和单轮签名两个阶段,如果有需要的话,这两个阶段可以合成一个完整的两轮协议。需要说明的是,签名过程中的伪造攻击要求恶意敌手在选择自己的承诺前看到其它节点的承诺份额或者自适应地选择签署的消息,从而操纵执行签名操作的节点集合生成的c。为了在不限制并发性的情况下防止伪造攻击,本方案“绑定”每个参与节点对特定消息的签名份额,以及用于签名操作的参与节点结合和他们的承诺。通过这种方式,结合不同消息或者参与节点/承诺对的签名份额将导致一个无效的签名。 预处理阶段的具体过程如算法2所示,在这一阶段,参与节点一次性生成并发布π个承诺,因此,π决定了在一次预处理过程中生成的随机数数量和他们对应的承诺。每个参与节点Oi首先生成一个私有随机数对列表以及相应的公开承诺份额 其中,j是计数器,用于识别下一个可以用来签名的随机数/承诺份额对。然后发布 (i,Li), 其中Li是他们的承诺份额列表 算法2:预处理算法 (1)Li=[ ] (2)for 1≤j≤π (4) (Dij,Eij)=(gdij,geij) //计算承诺份额 (5)Li.append (Dij,Eij) (6) store ((dij,Dij), (eij,Eij)) (7)publish (i,Li) 在单轮签名阶段过程中,我们用SA表示签名合成者,它可以是任意一个签名参与者,设α(t≤α≤n) 为执行签名操作的参与节点数,S={o1,…,oα} 为这些参与节点的集合,对S使用拉格朗日差值法得到的节点oi的拉格朗日系数为 (1)SA从Li获取每个参与者oi∈S的下一个合法承诺并构建有序列表 B=〈(i,Di,Ei)〉oi∈S (2)SA向oi发送(m,B)。 (3)在收到(m,B)后,oi首先验证消息m,然后对B中的每个承诺,验证Dl,El∈G,任意一项验证不通过则退出算法。 (4)oi计算绑定值 ρl=H1(l,m,B)(ol∈S) 然后得到组承诺 R=∏ol∈SDl·(El)ρl (5)oi利用密钥份额si计算他们的签名份额 zi=di+(ei·ρi)+λi·si·c 其中,用S来确定第i个拉格朗日系数λi。 (6)oi从本地删除 ((di,Di), (ei,Ei)), 然后向SA返回zi。 (7)签名合成者SA执行以下操作: 1)对于oi∈S,获取 ρi=H1(i,m,B) 然后计算 R=∏oi∈SRi 2)通过以下等式对每一个签名份额zi(oi∈S) 进行验证 3)如果等式不成立,则识别并报告该问题节点,然后退出算法,否则继续 4)计算 z=∑zi 5)得到完整数字签名 σ=(R,z) 2.3.3 签名验证 链下预言机共识方案的目标是将链上沟通需求降至最低,即对于执行同一数据请求的一组预言机,只由一个预言机返回数字签名σ,只产生一条链上消息。但是在实际操作中,由于签名不会立即发布到区块链上,多个预言机节点可以独自将签名结果发送到区块链。 因此,为了避免重复发送消息,我们从最终达成共识的α台预言机中根据随机数算法随机选举出一个预言机节点作为聚合预言机,向预言机智能合约提交数据D及其完整的数字签名σ=(R,z), 预言机智能合约接收到签名信息后,利用全局公钥Y对其进行验证,验证公式为 gz=RYc 如果验证不通过,则说明消息已经被篡改;如果验证通过,则说明数据真实可靠。验证通过后,预言机智能合约通过回调函数将数据D发送给数据请求智能合约。 2.3.4 预言机奖励 完成数据共识和数据结果反馈后,预言机智能合约根据集合Ci中各预言机节点提交的commi情况对真实获取了数据产生部分门限签名的预言机节点进行奖励,具体的奖励算法如算法3所示。 算法3:预言机奖励算法 (1)等待收到n-f个不同的预言机提交集合(Ci)的集合C (2) for every oracleOido (3) ifσi∈PS&>2f个提交集合从Oi提交了σi (4) sendrewardtoOi (5) end if (6) end for (1)门限签名正确性 证明 原式得证。 定理2σ=(R,z) 是对消息m的正确签名。 然后让F3(x)=F2(x)+c·F1(x), 其中c=H2(R,Y,m)。 因此,zi=di+(ei·ρi)+λi·si·c=λi(F2(i)+c·F1(i))=λiF2(i), 所以z=∑oi∈Szi相当于是F3(0)=(∑oi∈Sdi+eij·ρi)+c·s的拉格朗日插值。因为R=g∑oi∈Sdi+ei·ρi,c=H2(R,Y,m), 因此σ=(R,z) 是对消息m的正确签名。 (2)预言机奖励算法正确性 定理3 预言机奖励算法不会奖励吃空饷的预言机节点。 证明:假设预言机节点Oz在“吃空饷”。则只能在T时间之后才能广播合法结果,T时间指首个诚实节点在算法1的第(9)步取消提交的时间。Oi收到了n-f条prepared 信息,其中至少n-2f条信息来自诚实节点。Oj指代上述n-2f个诚实节点的其中一个节点。Oj在发出prepared信息后不会再接收提交结果,因此任何此类诚实节点Oj的集合Cj在T时间后都不会再改变。所以,算法3中的C中最多有n-(n-2f)=2f个集合将包含Oz。因此Oz不会收到奖励。 (1)抗合谋攻击 利用(t,n)门限签名方案实现分布式预言机的链下共识,对于n个预言机节点的网络,至少需要t个节点合作才能生成完整的数字签名。也就是说只要发起签名的合法预言机节点数≥t,就不会对最终的共识结果产生影响,因此,假设O中有1≤x (2)抗伪造攻击 在门限签名方案中,恶意敌手可以在密钥生成阶段或者签名生成阶段进行欺骗和伪造攻击。在本文提出的方案中,首先在密钥生成过程中,我们要求每个参与的预言机节点通过零知识证明来证明他们知道秘密值ai0,以防止在t≥n/2时的欺骗攻击。其次,在签名生成阶段,一方面,每个节点必须用密钥份额si来计算签名份额zi,而密钥份额由每个节点自行保管的,根据公开信息时无法计算出其它节点的密钥份额;另一方面,本方案“绑定”每个参与节点对特定消息的签名份额,以及用于签名操作的参与节点集合和他们的承诺,这样,结合不同消息或者参与节点/承诺对的签名份额将导致一个无效的签名。最后,不管是在密钥生成阶段还是签名验证阶段,我们都通过相应的验证等式对密钥份额和签名份额进行验证,如果验证不通过,则说明本次签名异常,终止协议。 为了验证本方案提出的分布式预言机共识机制的可用性和有效性,我们对区块链网络带宽占用率和预言机网络共识时间分别进行实验和统计,并与其它方案和算法进行对比。 3.3.1 带宽占用率 分布式预言机链下共识方案设计的一大目的就是减少预言机网络和区块链之间的通信次数,减轻区块链网络带宽压力。因此,我们首先比较了本文提出的分布式预言机链下共识方案和传统的链上共识方案下区块链网络的带宽占用率,我们将用户发送的请求数量从100增加到1000,设置参与共识的预言机节点个数为5,区块链网络带宽为100 Mbps,同时固定上传到区块链的每条消息大小为10 kb,记录区块链网络的带宽信息。结果如图3所示,可以看出,随着请求数量的增加,这两种方案下占用的网络带宽都呈上升趋势,但是从整体上来看,在本文所提出的链下共识方案下,网络带宽占用率在所有请求数量下均明显高于链上共识方案,并且随着请求数量的增加,这两种共识方案之间的带宽占用率差距越来越大。 图3 带宽占用率对比(链上共识vs链下共识) 3.3.2 共识时间 我们通过共识时间来对共识效率进行衡量,较低的共识时间表示预言机网络可以快速达成共识,数据传输的安全性更高,同时用户等待的时间也更少。在本研究中我们测量的共识时间为各预言机节点完成数据获取到达成共识将数据结果反馈到预言机智能合约的时间。 (1)链上共识与链下共识 首先我们对传统的链上共识和本文所提出的链下共识方案进行对比,图4展示了预言机节点数从增加至5增加至50时,分布式预言机网络达成共识所需时间的比较。从图4可以看出,相较于链上共识方案,本文所提出的链下共识方案达成共识所需的时间更短,同时随着预言机数量的增多,二者共识时间差值越大。 图4 共识时间对比(链上共识vs链下共识) 然后我们进一步对这两个方案在密钥生成、签名生成和签名验证这3个阶段的耗时进行分析和对比,结果如图5所示,左列为链上共识方案,右列为链下共识方案,从图中可以看出,在密钥生成和签名生成阶段,这两个方案所需的时间相差不大;但是在签名验证阶段,链下共识方案所需的时间明显少于链上共识方案,并且随着预言机数量的增加,链上共识方案耗时出现了明显的增加,但是链下共识方案的耗时则基本保持不变,这是因为链下共识方案只将共识后的数据结果发送至区块链,也就是说,不管有多少预言机节点参与共识,最终只上传一个数字签名,也只需要对该签名进行验证。 图5 各阶段耗时对比(链上共识vs链下共识) (2)ECDSA门限签名与Schnorr门限签名 不同的签名算法对应的门限机制实现复杂度和效率是不同的,除了本文提出的基于Schnorr签名算法的门限签名方案外,基于ECDSA签名算法的门限签名方案也十分常见,而ECDSA也是比特币和以太坊采用的交易签名算法。因此我们进一步对这两种方案进行对比。 我们主要关注这两种签名算法在基于DKG协议和多方计算的原理去生成和分发签名算法中需要的秘密值的过程中的差异。因此,我们主要测量了当预言机节点数从增加至5增加至50时,密钥生成阶段所需的时间。 从图6可以看出,Schnorr门限签名在密钥生成阶段的耗时明显少于ECDSA门限签名算法,这是由于ECDSA签名算法中秘密值k是非线性的,所以在分布式密钥生成与分发过程的实现上更为复杂,效率也更低,而Schnorr门限签名算法在生成和分发签名算法所需的私钥碎片时计算量更小,因此速度更快,效率更高。 图6 密钥生成阶段耗时对比(ECDSA门限签名vs Schnorr门限签名) 利用区块链和预言机技术实现海量电力数据的可信传输与存储是未来电力数据管理重要的发展方向。而在利用分布式预言机进行数据获取与共识的过程中,现有的预言机链上共识方案存在区块链网络压力大、共识效率低等问题,因此本文基于(t,n)门限签名技术和Schnorr签名算法,提出一种面向智能电网的分布式预言机链下共识方案。该方案由密钥生成、签名生成、签名验证和预言机奖励4个阶段构成,各预言机节点在链下通过分布式协作生成部分签名并聚合成完整的可验证签名。与现有的分布式预言机链上共识方案相比,本方案在减缓区块链网络压力、提升系统运行效率的同时具有良好的正确性和安全性,同时对系统功能的实验和测试验证了方案的高效性。





c=H2(R,Y,m)
Ri=Dij·(Eij)ρi
c=H2(R,Y,m)3 方案分析
3.1 正确性分析




3.2 安全性分析
3.3 性能分析



4 结束语

