基于两阶段搜索的密度聚类算法
汪 勇,李巧娜,艾学轶
(武汉科技大学 恒大管理学院,湖北 武汉 430081)
0 引 言
密度聚类是应用广泛的一类机器学习方法。典型的密度聚类算法有DBSCAN[1]和DPC[2]。DBSCAN算法两个参数凭经验确定,易形成过度聚类或噪声增多问题。另外,核心对象的随机选择影响聚类的稳定性。为此,Ankerst提出基于任何半径和阀值的聚类方法OPTICS[3],该方法生成一个簇排序可达图,将参数隐含在图形中,由应用者根据需要选择聚类结果,这给应用者带来极大不便。于是,一些改进的算法如基于动态近邻的DN-DBSCAN算法[4]、高效处理簇密度的RNN-DBSCAN算法[5]、自适应邻域的AA-DBSCAN算法[6]以及解决离群数据点聚类问题的VDBSCAN算法[7]等相继被提出,在一定程度上提高了DBSCAN的聚类性能。基于对密度聚类方法思想的延伸,Rodriguez等在Science上发表论文提出密度峰聚类算法(DPC)。虽然DPC算法只有一个计算局部密度的截断距离参数,但该参数值确定依然无据可依,基于距离的最近邻划分聚类策略易产生错误聚类。为此,研究者提出一些改进的密度计算方法,提高密度峰值的差异性,如采用邻域数据点残差计算局部密度的REDPC算法[8]。计算相对密度的RDCA聚类算法[9]、基于逻辑分布和引力的密度计算方法DPC-LG[10]和自适应密度峰聚类算法[11]等。针对连带错误聚类问题,研究者提出一些改进的聚类策略,如模糊加权k近邻算法[12]、指数样条k近邻算法[13]以及相互邻近度划分聚类算法[14]等,较好地解决了连带错误聚类问题。
在上述密度聚类算法研究基础上,本文提出一种基于两阶段搜索的密度聚类算法(density clustering algorithm based on two-stage search,DCATS),进一步提高其聚类精度。
1 DCATS聚类思想
1.1 基本概念定义
给定数据集DS={x1,x2,…,xn}, 其中xi={xi1,xi2,xim},i=1,2,…,n,n为数据数量,m为数据维度。设ε是一个正数,则开区间 (xi-ε,xi+ε) 为数据点xi的ε邻域。
定义1 数据点xi的密度ρ(xi)是xi邻域ε内的数据点数量,即
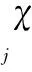
(1)
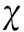
定义2 所有数据点按照密度由高到低排列,按式(2)计算相对密度差d(xi),令具有最小相对密度差绝对值之和的密度为δ,则称δ为密度阈值。当ρ(xi)≥δ时,xi为高密度数据点。否则,xi为低密度数据点
(2)
定义3 设xj在xi的ε邻域内,且xi是高密度数据点,则称xj是xi的直接密度可达点。设xj为高密度数据点,xk是xj的直接密度可达点,若xk是高密度数据点,则称xk是xi关于邻域ε和δ的密度可达点。否则,称xk是xi的密度相连点。
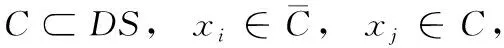
dik-dij>0
(3)
1.2 两阶段搜索
DCATS由邻域递归搜索和簇最近邻搜索两个阶段组成。第一阶段,邻域递归搜索(recursive search in neighborhood,RSN)采用递归搜索方法,在高密度数据点邻域内搜索未聚类的直接密度可达点、密度可达点和密度相连点,并将这些数据点归为该高密度数据点所在的簇。直到搜索到的数据点均已聚类或均为低密度数据点为止。RSN搜索流程如图1所示。

图1 邻域逆归搜索阶段
图1中,条件1判断密度排序数据集是否含有未聚类的高密度数据点。条件2判断每次搜索的数据点中是否含有高密度数据点。
第一阶段聚类完成时可能存在未聚类的低密度数据点,此时,启动第二阶段的簇最近邻搜索算法(search the nearest neighbor in cluster,SNNC),实现低密度数据点或离群数据点聚类。在已聚类数据簇中搜索距离未聚类的低密度数据点最近的数据点,即簇最近邻点,根据簇最近邻距离与邻域关系以及当前已聚类簇数,确定该低密度数据点的归属。簇最近邻搜索流程如图2所示。
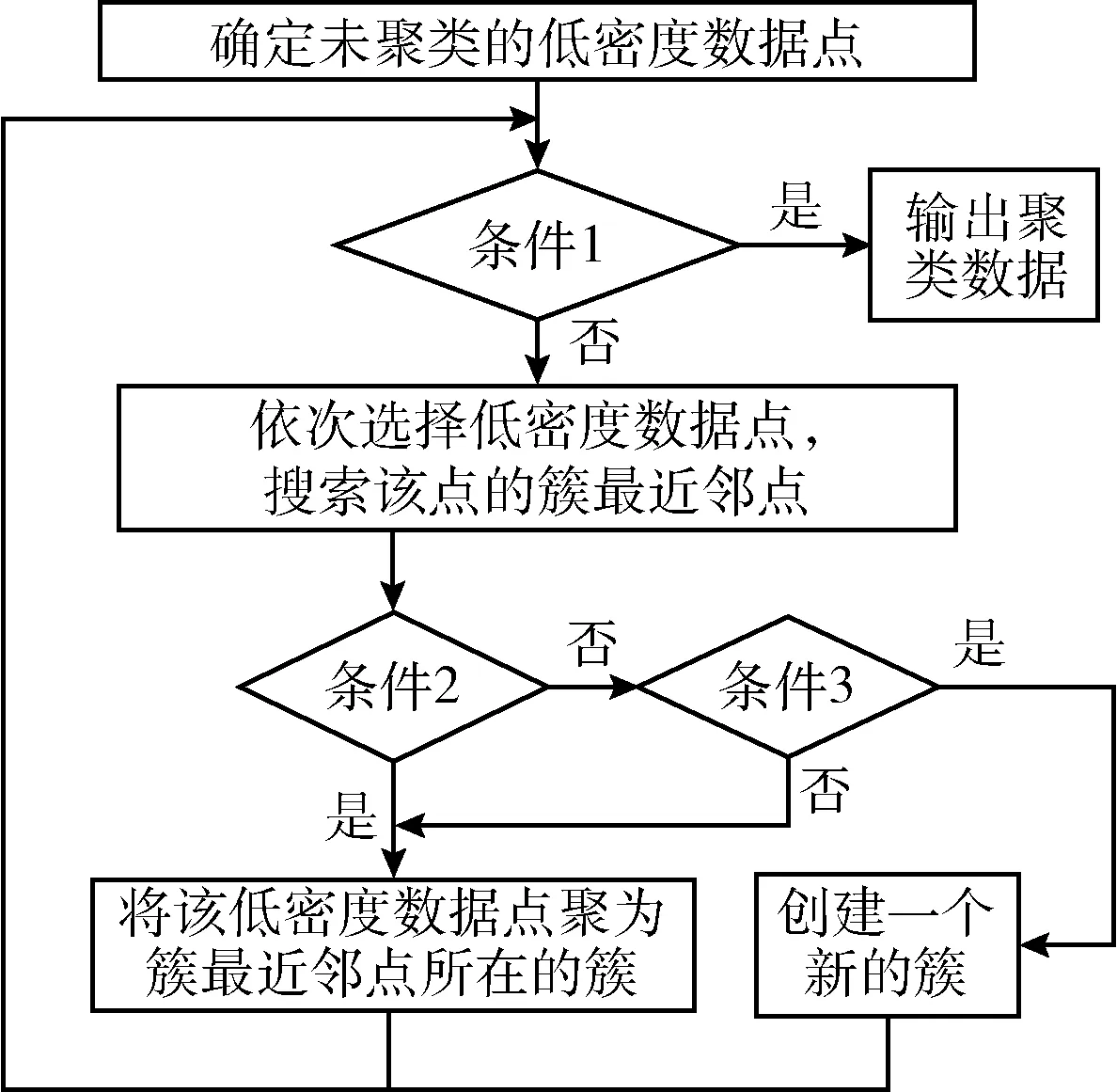
图2 簇最近邻搜索阶段
图2中,条件1判断所有低密度数据点是否均已聚类。条件2判断簇最近邻距离是否小于等于邻域。条件3判断当前聚类是否只有一个簇。
2 DCATS算法设计
2.1 聚类策略
DCATS运用密度排序、簇最近邻分配和自适应搜索方法设计算法的聚类策略。
(1)密度排序
对于DBSCAN,假设xi和xj为随机排列的两个核心点,且xi和xj分属于不同簇,dij>ε。数据点xk为非核心点,dik≤ε,djk≤ε。若xi排列在xj之前,则xk属于xi所在的簇,否则,xk属于xj所在的簇。故xk的归属具有随机性。DCATS将所有数据点按密度由高到低排序,构成密度序列,RSN从第一个高密度数据点创建类簇进行聚类,SNNC从第一个低密度数据点搜索簇最近邻点。密度排序策略解决DBSCAN聚类的稳定性问题。
(2)簇最近邻分配
对于给定的未聚类数据点,其簇最近邻与最近邻的区别是,簇最近邻为已聚类数据点,而最近邻可能是已聚类数据点,也可能是未聚类数据点。SNNC根据低密度数据点与其簇最近邻点的距离以及邻域关系确定该低密度数据点的归属。当低密度数据点与簇最近邻之间距离小于等于邻域时,将该低密度数据点归类到其簇最近邻所在的簇。当其距离大于邻域时,分为两种情形,若当前聚类簇数为空或只有一簇时,则以该数据点创建一个新的簇。否则将该数据点归类到其簇最近邻所在的簇。
(3)自适应搜索
自适应搜索是指DCATS根据邻域和数据分布情形而自动选择执行RSN和SNNC实现聚类。当数据点均匀分布时,根据设置的邻域,所有数据点均为高密度数据点或低密度数据点,DCATS只启动RSN或SNNC即可完成聚类。对于连续变密度数据,则同时启动RSN和SNNC进行两阶段搜索聚类。
2.2 符号说明
DCATS算法涉及的符号见表1。

表1 符号说明
2.3 算法描述
2.3.1 RSN算法
采用密度排序和自适应搜索策略设计RSN算法,算法描述如下。
(1)给定数据集DS,设置邻域eps。
(2)按式(4)计算DS两数据点之间的距离d并按距离升序排列
(4)
(3)按式(1)计算数据点xi的密度DP(xi),并按密度降序排列。
(4)按式(2)计算数据点xi的相对密度差绝对值之和,选择最小值的数据点密度作为密度阈值DenThd。
(5)设置数据点编号SN、聚类输出矩阵C和各簇数据点数累积值Q。SN为按密度排序的数据点编号。
(6)判断SN的状态,若SN不为空且DP(1)≥DenThd, 转下一步,否则转SNNC算法。
(7)以数据点SN(1)创建一个簇并将其存入C。令高密度数据点HDP初始值为SN(1),删除SN(1)。
(8)若HDP不为空,转下一步,否则转步骤(6)。
(9)查找HDP邻域内不重复且未聚类的数据点Pts并将其存入C,删除SN中数据点Pts。
(10)累积已聚类数据点数量并存入Q。
(11)按定义4查找Pts中的高密度数据点,生成新的HDP,转步骤(8)。
2.3.2 SNNC算法
采用密度排序、簇最近邻分配和自适应搜索策略设计SNNC算法,算法描述如下。
(1)判断所有数据点是否为低密度数据点。若C为空,表示所有数据点为低密度数据点,即DenThd>DP(1,2), 转下一步。否则转步骤(3)。
(2)将SN(1)添加至C,创建一个簇,删除SN(1)。
(3)统计SN中余下的低密度数据点数量L,令i=1。
(4)若i≤L,转下一步。否则聚类结束,输出聚类数据C。
(5)从dist中提取与数据点SN(i)构成的点对A,统计A的点对数量S,令j=1。
(6)若j≤S,转下一步。否则i=i+1,转步骤(4)。
(7)在A中查找距离SN(i)最近的点对A(j,2)。
(8)若A(j,2)属于C,由式(3)可知,A(j,2)是SN(i)的簇最近邻,转下一步。否则j=j+1, 转步骤(6)。
(9)统计当前已聚类的簇数nc。
(10)若SN(i)与A(j,2)之间的距离A(j,3)≤eps, 转下一步。否则,若nc=1,转步骤(14)。否则转下一步。
(11)查找A(j,2) 在类簇C中的位置并将SN(i) 插入到C的A(j,2) 之前的位置。
(12)查找A(j,2) 位置值在Q中的位置。
(13)更新C中各类簇数据点累积数。i=i+1, 转步骤(4)。
(14)将SN(i)添加到C的尾部,构成新簇,转步骤(13)。
2.4 时间复杂度
由RSN算法步骤可知,它由距离计算、密度计算和邻域搜索过程组成。数据点距离计算次数为n(n-1)/2, 故时间复杂度为O(n2)。 显然,密度计算的时间复杂度为O(n)。 邻域搜索是一个递归过程,假设聚类为c簇,数据点数量分别为n1,n2,…,nc, 则时间复杂度为
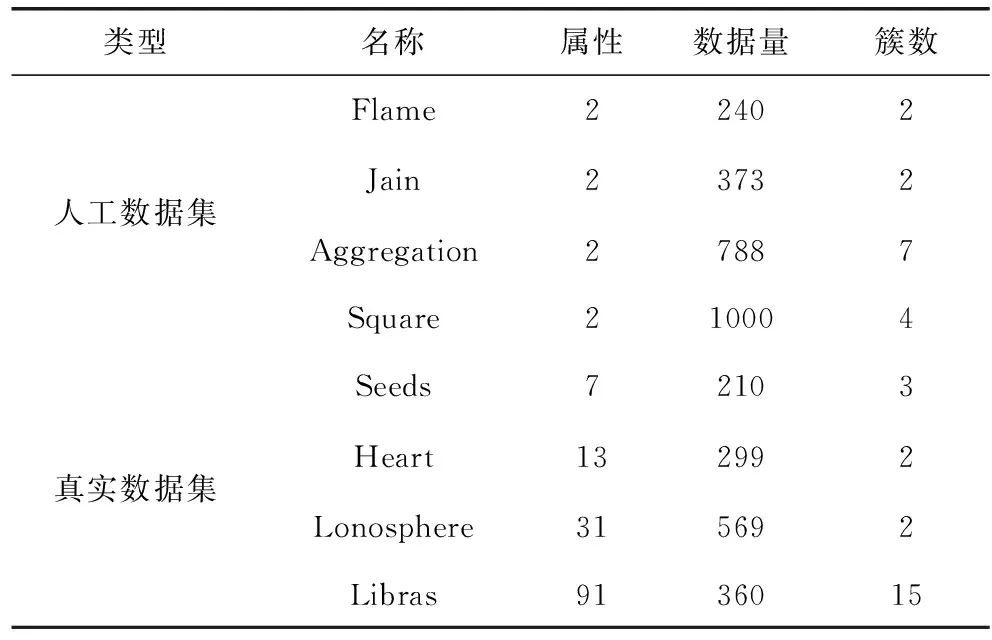
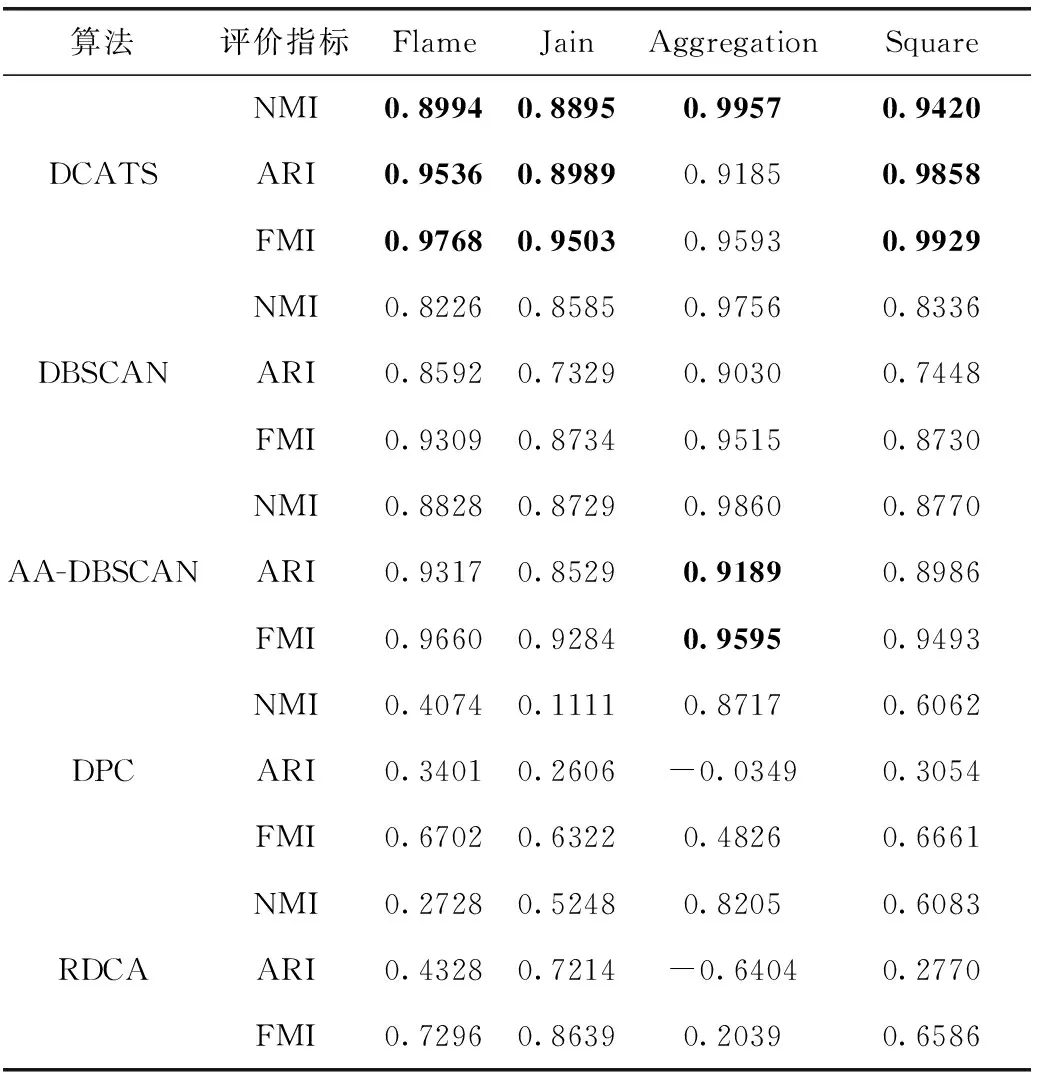
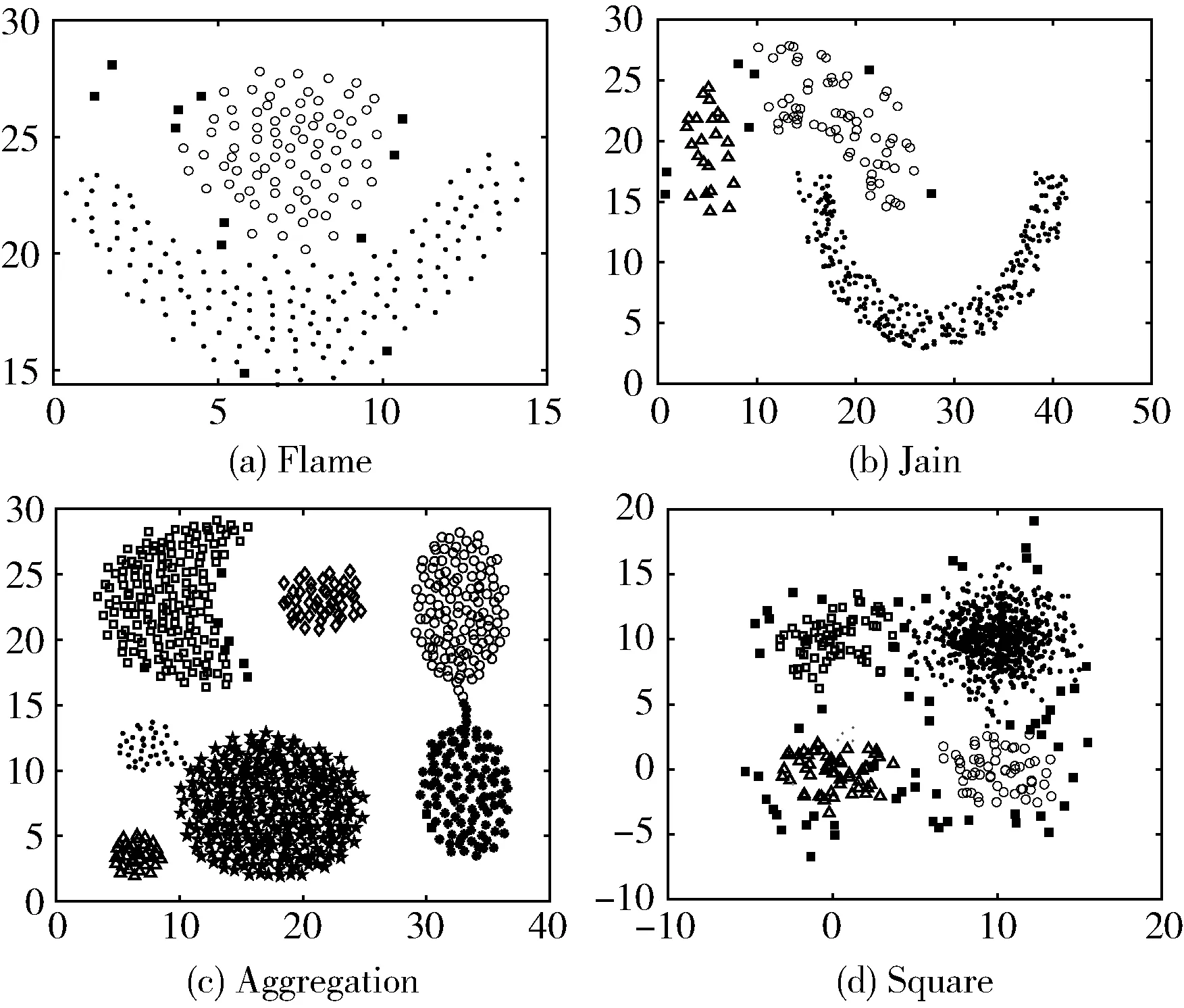
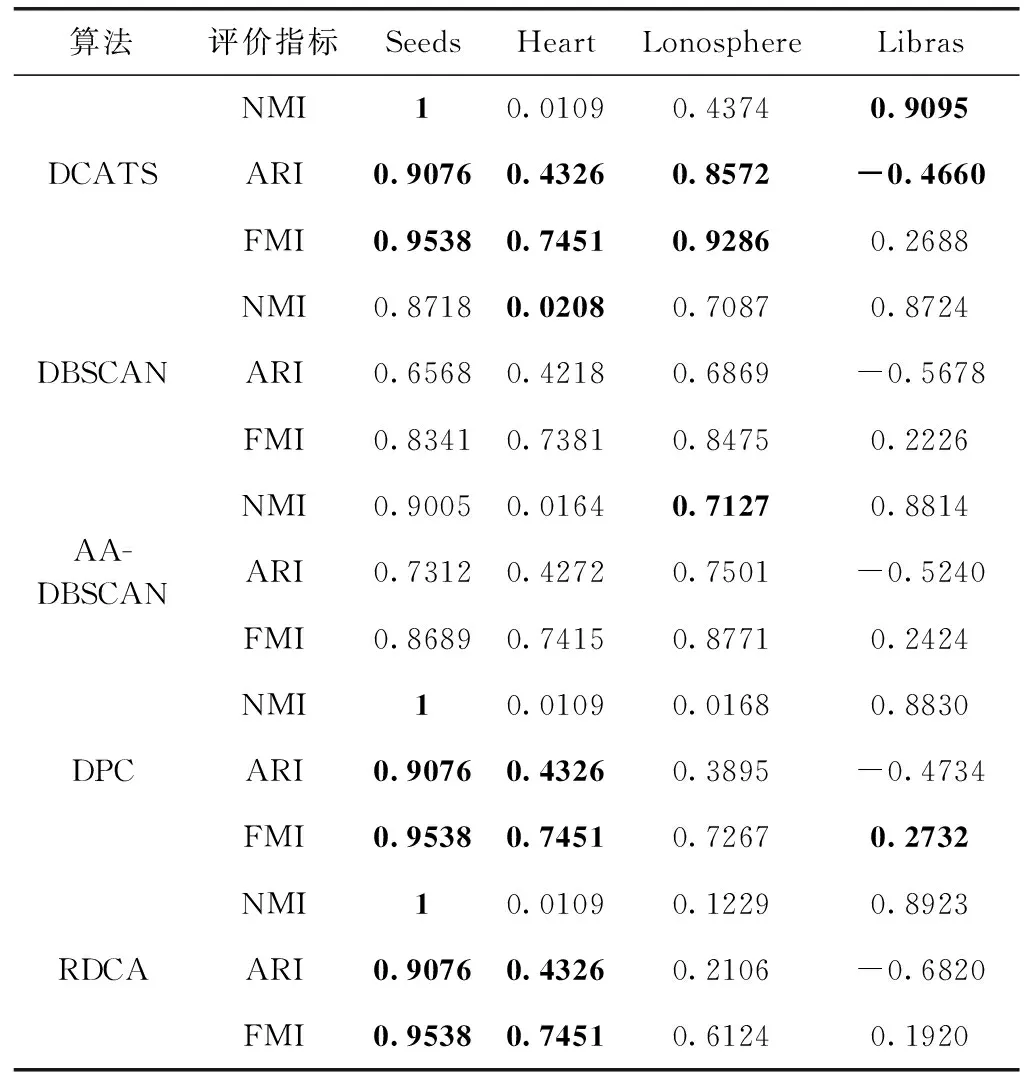
O(logn1+logn2+…+lognc) (5) 对于SNNC算法,最坏情况下,假设剩余的数据点有n个,因d是有序的,故只需n次搜索即可完成聚类,时间复杂度为O(n)。 由上述分析可知,距离计算是DCATS算法执行最耗时的过程,与DBSCAN和DPC算法一样,DCATS时间复杂度为O(n2)。 为验证DCATS聚类算法性能,选择4个人工数据集和4个UCI真实数据集进行测试[14]。数据集描述见表2。 表2 数据集描述 将DCATS与DBSCAN、AA-DBSCAN[6]、DPC和RDCA[9]进行聚类效果对比。利用标准互信息(NMI)[15]、调整兰德系数(ARI)[16]和Fowlkes-Mallows指数(FMI)[17]评价各算法的聚类效果。采用Matlab作为实验平台,经多次实验选择最优参数作为各算法的聚类参数。 5个算法在4个人工数据集上的聚类结果评价指标见表3。粗体数值表示对应的指标最优。 表3 人工数据集聚类评价 由表3可知,对于Flame、Jain和Square这3个数据集,DCATS这3个指标保持最优。对于Aggregation数据集,DCATS的NMI指标最优,AA-DBSCAN的ARI、FMI指标略优于DCATS。总的来看,AA-DBSCAN和DBSCAN聚类效果优于DPC和RDCA,AA-DBSCAN优于DBSCAN,RDCA优于DPC,DCATS算法聚类效果优于比较的4个算法。各算法在4个人工数据集上的聚类结果如图3~图7所示。 图3 DCATS聚类结果 图4 DBSCAN聚类结果 图5 AA-DBSCAN聚类结果 图6 DPC聚类结果 图7 RDCA聚类结果 图3(a)~图7(a)是Flame数据集的聚类结果。5个算法均聚为2簇,DBSCAN和AA-DBSCAN存在少数噪声点,且AA-DBSCAN噪声点少于DBSCAN。DPC和RDCA出现明显的连带错误,聚类结果较差。只有DCATS聚类结果最理想。 图3(b)~图7(b)是Jain数据集的聚类结果。DCATS、DBSCAN和AA-DBSCAN聚为3簇,DBSCAN和AA-DBSCAN出现少量噪声点。DPC和RDCA虽聚为2簇,但存在较多的错误聚类。总的来看,DCATS在Jain数据集上的聚类结果最好。 图3(c)~图7(c)是Aggregation数据集的聚类结果。5个算法均聚为7簇。AA-DBSCAN噪声点少于DBSCAN。DPC和RDCA均有3簇出现错误聚类。总的来看,对于Aggregation数据集,前3个算法聚类结果相近,DCATS算法聚类结果更优。 图3(d)~图7(d)是Square数据集的聚类结果。DBSCAN和AA-DBSCAN出现较多的噪声点,DPC和RDCA均存在簇间错误聚类。相对而言,DCATS在Square数据集上的聚类结果明显优于另外4个算法。 真实数据集均为多维度数据。5个算法在4个真实数据集上的聚类结果评价指标见表4。粗体数值表示对应的指标最优。 由表4可知,对于Seeds数据集,DCATS、DPC和RDCA这3个指标相同,均为最优。对于Heart数据集,DCATS、DPC和RDCA的ARI和FMI指标相同,均为最优,DBSCAN的NMI指标最优。对于Lonosphere数据集,DCATS的ARI和FMI指标最优,AA-DBSCAN的NMI指标最优。对于Libras数据集,DCATS的NMI和ARI指标最优,DPC的FMI指标略优于DCATS。综合来看,DCATS算法的聚类精度优于比较的密度聚类算法,表明其聚类策略是有效的。 表4 真实数据集聚类评价 DCATS对所有数据按密度进行排序,第一阶段的邻域递归搜索算法代替DBSCANs基于核心对象的邻域搜索机制,避免DBSCANs核心对象的选择顺序造成数据点随机聚类问题,实现数据的稳定聚类。同时,邻域递归搜索算法自动确定类簇,避免DPCs聚类算法人工确定聚类中心带来的主观聚类问题。DCATS的簇最近邻搜索算法实现低密度离群数据点的正确聚类,消除DBSCANs聚类产生的噪声数据点。同时,簇最近邻搜索算法解决了DPCs的最近邻划分策略产生的聚类连带错误问题,提高了聚类精度。如何合理确定DCATS的邻域参数值得进一步探讨。3 算法性能分析
3.1 数据集选择
3.2 人工数据集测试




3.3 真实数据集测试
4 结束语

