面向NOMA视频多播的缓存和频谱分配
唐 昊,吉晓祥,沈 航,田一博,白光伟
(南京工业大学 计算机科学与技术学院,江苏 南京 211816)
0 引 言
随着视频需求的爆炸式增长,用户的视频质量难以得到保障。需要一系列的方法来解决这个问题:非正交多址接入(non-orthogonal multiple access,NOMA)被用来提高视频资源利用率(NOMA定义和优势请参见文献[1-5])。多播(mobile broadcast system,MBS),被用来向大规模的用户群传递多媒体流量。但是,信道条件最差的终端(如小区边终端)会成为资源分配的瓶颈,因为需要保证多播组内每个终端接收到的视频内容被正确解码[6]。利用可伸缩视频编(scalable video coding,SVC)和可扩展高效视频编码将视频流编码为一个基视频层和多个增强视频层,从而根据实际需求动态调节视频质量。这些视频层被自适应地调制以适应不同信道条件。在视频多播方案中引入SVC,以缓解由于信道条件较差的终端[7-13]带来的瓶颈影响。
为了解决多组资源分配和组内可伸缩组播调度问题,文献[14]提出了一种用于蜂窝网络下基于NOMA的SVC视频多播方案。该方案将SVC的连续视频层编码与NOMA的SIC译码相结合,使不同的视频层在功率域上分离,在相同的无线电资源上传输。为了提高基站缓存空间的利用率,文献[15]提出了一种缓存分区算法以获得最优的缓存空间分配策略,在此基础上提出了一种联合内容放置和用户关联算法,以实现所有内容请求用户的最小服务延迟。无线网络下,频谱资源和分层视频缓存的分配都会影响多播组的整体视频质量。因此,如何优化无线网络下面向NOMA无线视频多播的内容缓存和频谱分配策略,提升多播组用户的服务质量值得进一步探讨。
本文提出面向NOMA无线视频多播的内容缓存和频谱分配策略,综合考虑频谱资源、功率和分层视频缓存的分配。在本文中,考虑可扩展视频编码流在缓存支持的无线网络上的联合视频放置问题。将频谱、功率和分层视频缓存资源分配问题转化为一个混合整数线性规划问题。将该优化问题解耦为组内频谱约束与缓存约束的资源分配问题。在满足用户服务质量的前提下,以分层视频缓存策略为重点,提出基于动态规划的求解方法。设计面向多播组的峰值信噪比(peak signal-to-noise ratio,PSNR)优先算法和多播组内分层内容缓存算法来求出最优解。仿真结果表明,与现有方案相比,该方案可以显著提高用户接收视频的质量,提高资源利用率。
1 系统模型
如图1所示,考虑了一个基站服务K个多播组的无线蜂窝网络场景。基站缓存资源数量和频谱资源分别表示为C和f,基站发射功率被表示为P。在该场景中对各多播组内用户进行无线视频分层缓存的多播。将第k(1≤k≤K) 个多播组的集合表示为gk,则K个多播组集合可以表示为G={g1,g2,…,gK}。 将第k个多播组所占的缓存集合可表示ck,则K个多播组集合可以表示为C={c1,c2,…,cK}。
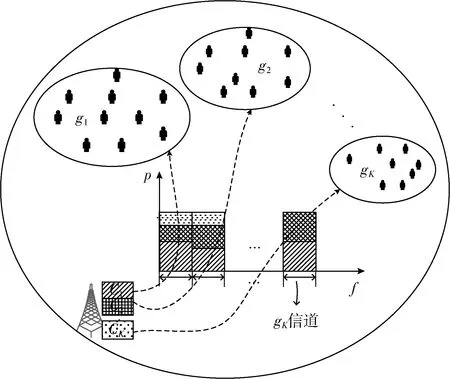
图1 面向NOMA无线视频多播的内容缓存和频谱分配
1.1 SVC视频流
每个多播组向基站请求分层缓存视频流。解码过程中,接收端可以利用基础视频层加上增强视频层重构视频。SVC视频解码必须在完成基础视频层解码的基础上,才能依次对增强视频层进行解码。lk用来表示第k个视频的层数,第k个视频第l个视频层的发送速率表示为λl,k。 接收端对视频解码必须逐层向上解码,否则较高的视频层无法被解码。在第k个多播组中的用户设备(UEi)接收到的有效视屏层数记为li,k。 终端接收到有效视频层的聚合速率可表示为
(1)
1.2 NOMA层
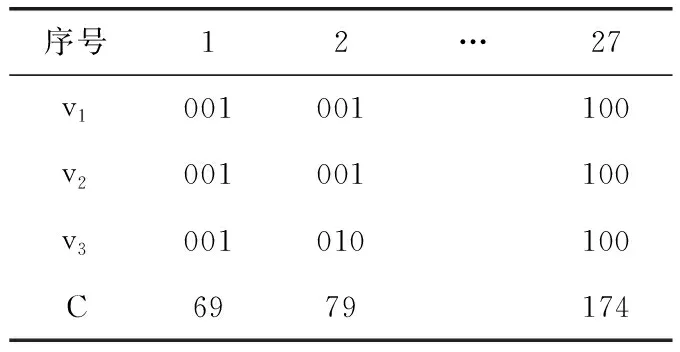
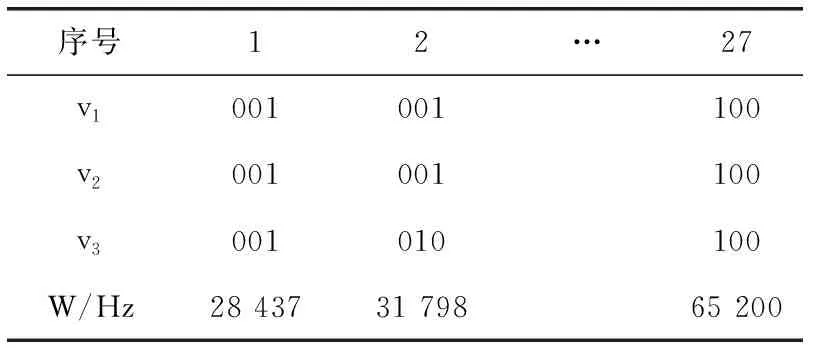
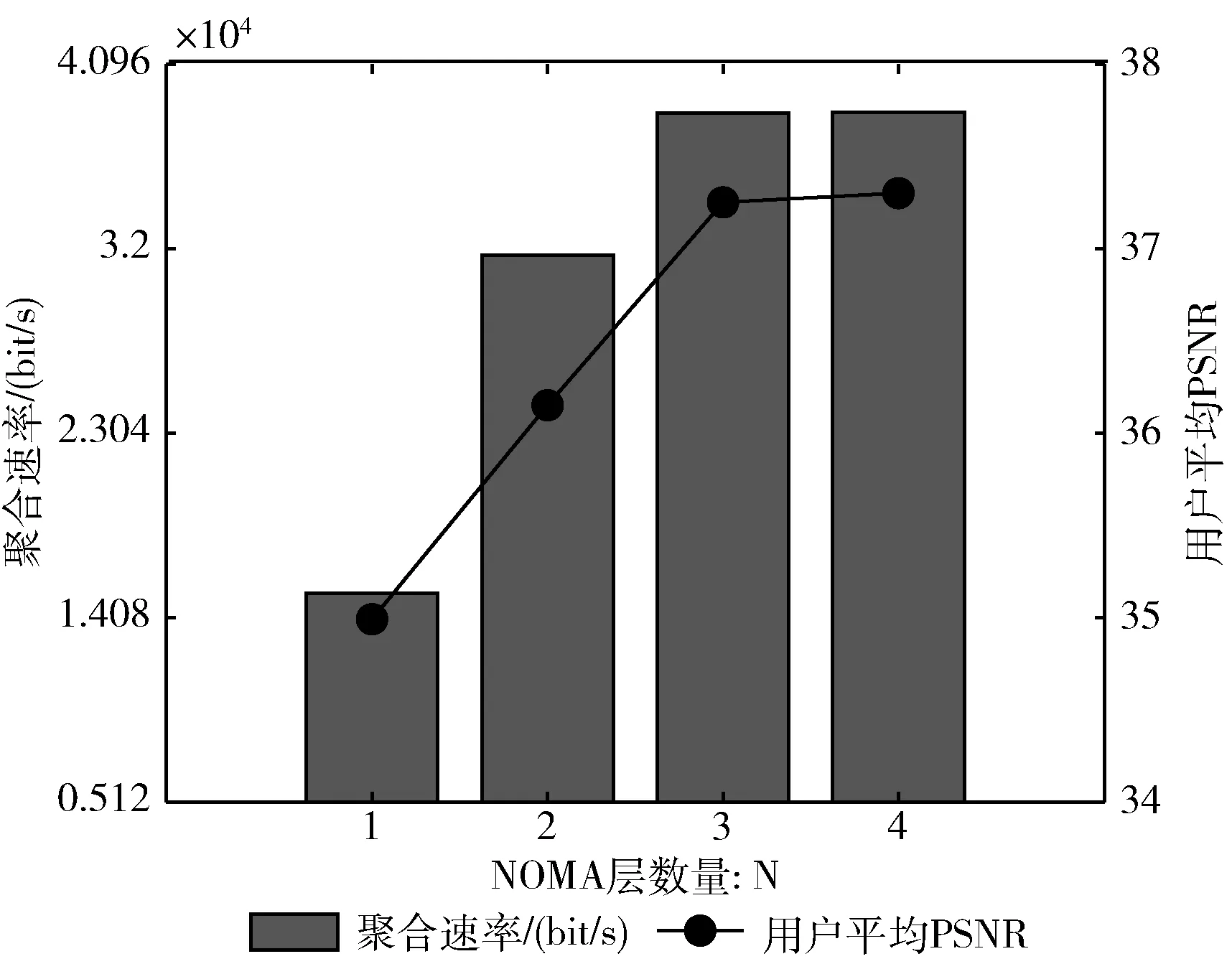
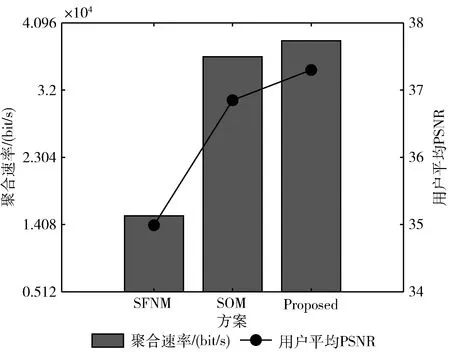
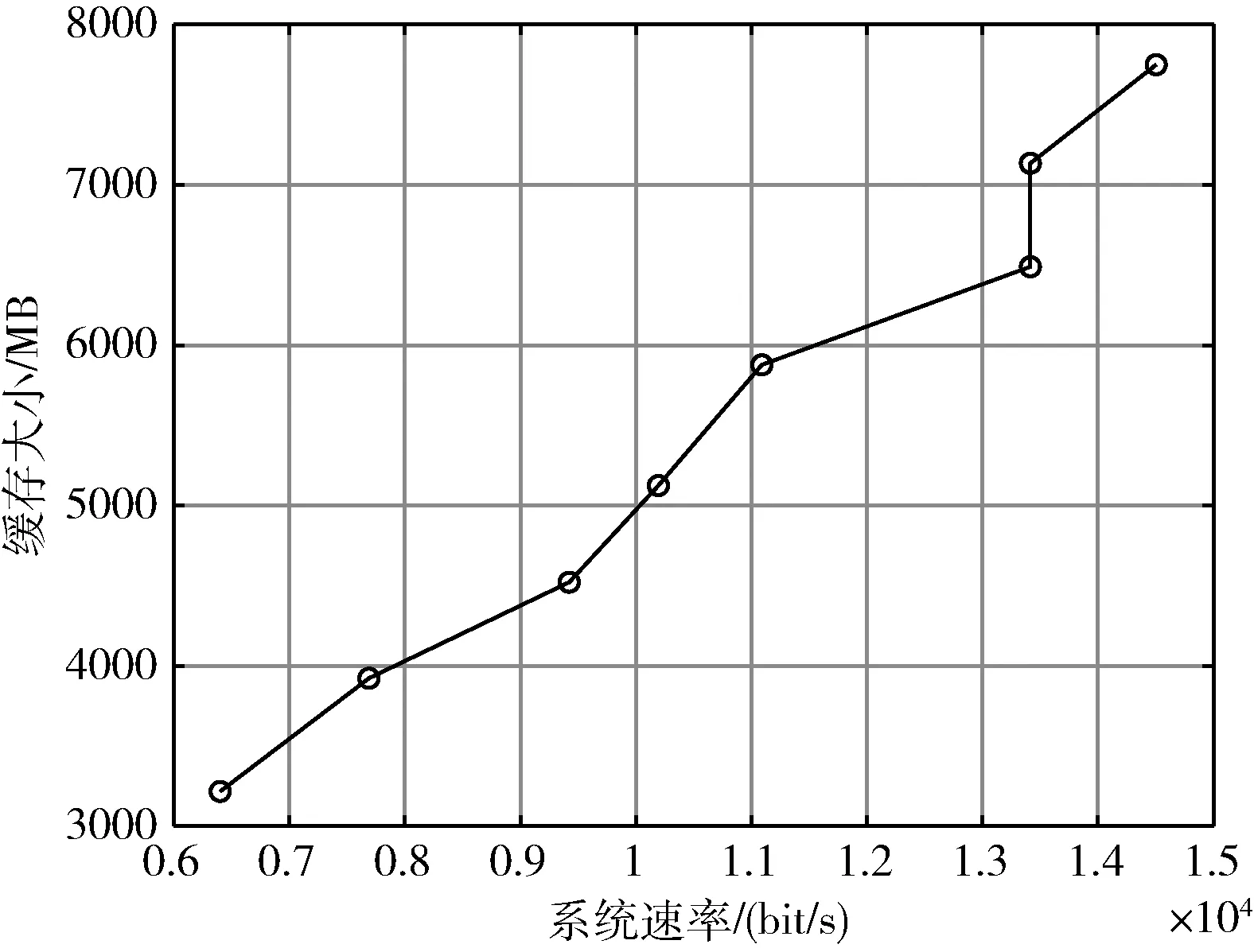
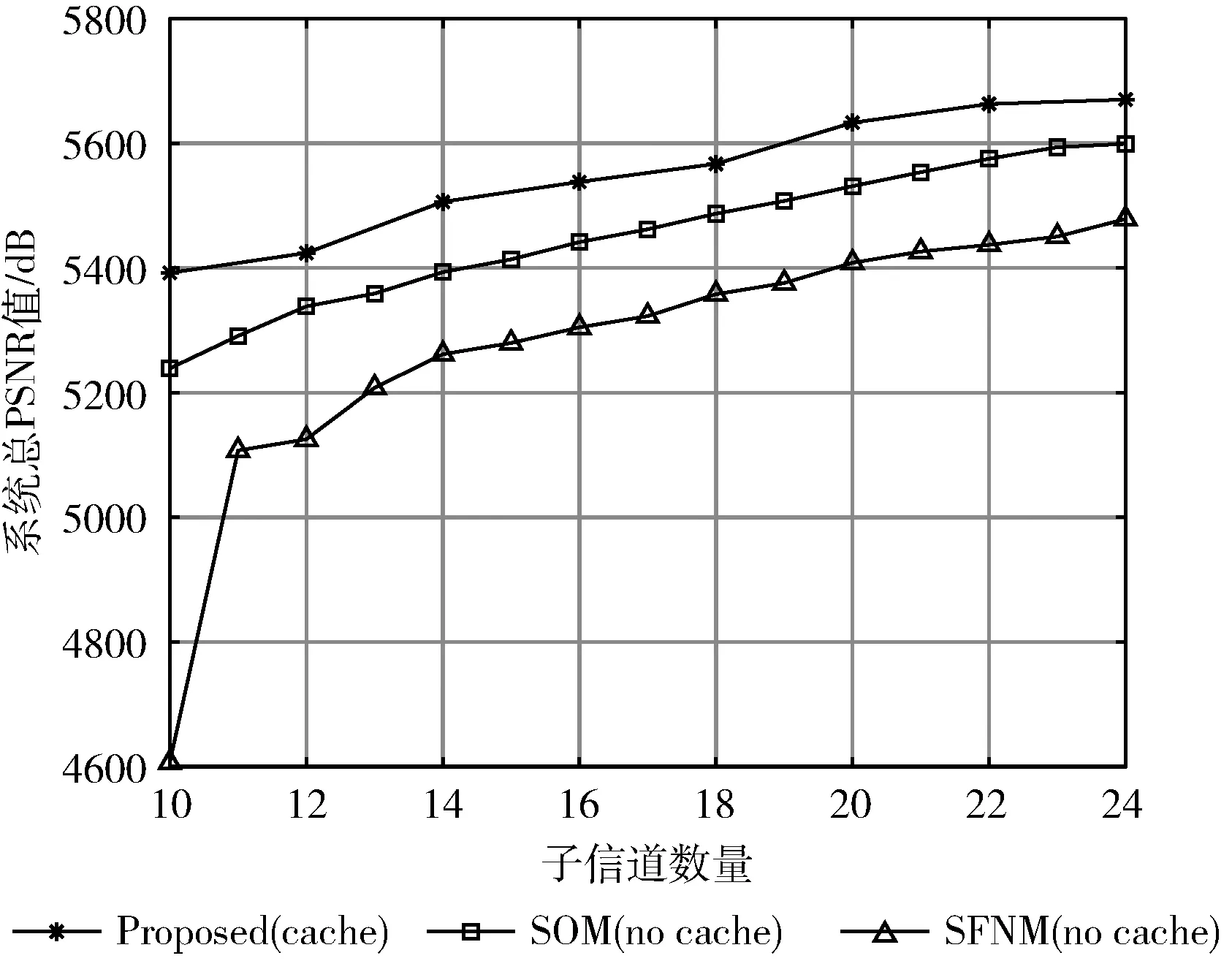
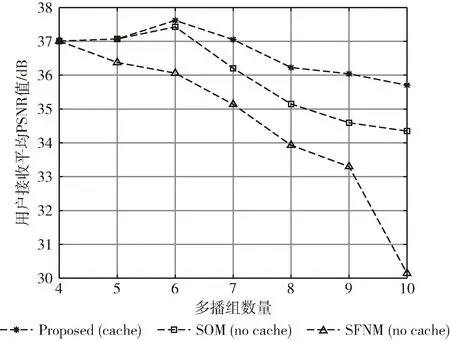
K个多播组有B个正交子信道,每个子信道的带宽为W,分配给第k组的子信道数为bk(∀1≤k≤K)。 在每一组中,NOMA在发射端采用叠加编码,在接收端采用SIC解码的功率域中实现不同终端的多路访问。假设NOMA层为NOMA叠加编码方案中的层,每组NOMA层数最大为N。对于第k组,第n(∀1≤n≤N) 个NOMA层的视频信号记为xn,k, 则用户设备的信道增益不低于hn,k的可解码。由于hn,k随着NOMA层数的增加而变大。所以这里NOMA层按所涉及终端信道增益的升序排列,即h1,k 根据NOMA原理,基站解码信号αm,k可以达到的最大传输速率为 (2) 其中 每个子信道的发射功率为P,噪声功率密度为N0。第n个NOMA层可实现的数据传输速率可以表示为 (3) 用户i接收时长为t的li,k视频所占缓存空间大小可表示为 (4) 如表1所示,假设基站向用户发送3个视频(v1、v2、v3),每个视频最高可以发送3个视频层。这里采用3×3的01矩阵进行遍历(001表示视频只发送基础层,以此类推),解出所有缓存方式所需要的空间,则视频放置的所有情况见表1。 表1 分层视频缓存和缓存空间/MB 如表1所示,这里给出一个关于频谱资源足够但缓存资源稀缺的案例,用于理解缓存资源对分层视频传输的影响。在缓存资源足够多的情况下,终端接收到的视频层数主要由频谱资源数量和分配策略决定。若基站缓存只有100 MB,有表1可以看出不是所有的分层视频缓存方案都能满足缓存需求,即每个多播组的缓存大小的总和不应超过总缓存大小,基站在分层视频缓存时应满足 (5) 这里给出一个关于缓存资源足够但频谱资源稀缺的案例,用于理解频谱资源对分层视频传输的影响,见表2。若只分配一个子信道给该多播组(bk的大小为40 kHz),由表2可以看出,不是所有分层视频传输方案都能满足带宽的约束,即每个多播组的带宽大小的总和不应超过总带宽大小,基站在分层视频发送时应满足 表2 视频放置方案和带宽资源/Hz (6) 基于面向NOMA无线视频多播的内容缓存和频谱分配策略,为每个NOMA层分配一定的功率用于信息的传输。当分配给NOMA层 (n,k) 的功率比例为αn,k时,可以达到的传输速率通过式(3)计算为rn,k。 为保证每个多播组分配NOMA层时产生的传输功率总和不超过基站的最大发射功率,即功率分配约束可表示为 (7) 在满足功率约束的情况下,还需满足信息传输约束。当δl,n,k=1时,表示第l个视频层可以在NOMA的 (n,k) 层传输。否则,δl,n,k=0。 则信息传输约束可以表示为 (8) 和 (9) 其中,式(8)限定任何视频层都不能在所有NOMA层中传输两次或两次以上。式(9)意味着在每个NOMA层中传输的信息比特率不能大于每个NOMA层中用户可以达到的最大传输速率,以保证实时视频内容可以被及时接收并流畅播放。 接收端通过SIC对接收到的信号进行解码。第k个多播组的UEi可以解码不高于 (ni,k) 的NOMA层。第k个多播组的UEi可以接收到的有效视频层数为 (10) 在NOMA无线视频多播内容的分层缓存和频谱分配的场景下,提出联合资源管理问题。在满足所有用户服务质量需求的基础上最大化系统的总PSNR,则联合资源管理问题可以表示为 其中,θi,k表示第k个多播组中第i个用户的PSNR值。 P0问题需要使用多维背包求解。为了便于处理,在考虑存储约束的情况下,将优化问题P0解耦为两个子问题P1和P2,并用背包算法进行求解。 若预先给定多播组的带宽资源bk,就可以求得该多播组的最优功率分配,从而得到该多播组的最大系统和PSNR。在此基础上进一步设计算法,并求解出问题最优解。将P0分为两个子问题 和 其中,P0等价于P2,其中θk被定义为P1对于任意ck的最优解。这是因为将正交资源分配给不同的组,当给定ck和c′k时,一组中变量的选择不影响另一组的选择。换句话说,不同组的子问题是相互独立的。 本文将P2分为两步求解:①给定每个视频所需带宽和PSNR,可以基站内PSNR最大时对应的分层视频发送方案;②将①输出的结果带入,求基站在满足缓存的约束下最大化系统PSNR。 首先,假设前k个多播组一共有b个子信道可用,使用函数f(k,b) 表示前k个多播组的最大系统PSNR。根据动态规划思想可得优化目标函数f(k,b), 即 f(k,b)=maxf(k-1,b-1)+θk (11) θk可以通过式P1得到,f(k,b) 通过多项选择背包算法求解。把K个多播组当作K类物品,装入一个容量为B的背包中。每类有B个项目,第k类的第bk个项目有利润θk和重量bk。那么f(k,b) 的实质是从每个类别中选择一部分,不超出背包总容量,使利润总和最大。 算法设计使用动态规划方法,当所有项的权值为非负整数时,求出背包问题的最优解,即f(k,b) 的最优解。首先,初始化f(k,b)=0,k=0表示没有多播组存在。然后,循环计算所有θk的值。接下来,从k=1开始递归地计算f(k,b), 在递归的每次迭代中,使用递归式(11)计算f(k,b), 其中f(k-1,b-b′) 在前一次递归迭代中已经计算过,θk在递归过程之前已经计算过。在KB次的迭代之后,可以获得了所有f(k,b) 的值。最后,返回f(K,B) 作为最优的系统PSNR,最后,返回f(K,B) 作为最优的系统PSNR,并使用矩阵X[J][l] 记下最优方案的选择方式,J表示满足约束的视频个数,l表示视频层数。流程如算法1所示。 算法1: 面向多播组的PSNR优先算法 Input:l,k,b,G={g1,g2,…gK} 输入: 可以发送的最高视频层数l, 多播组数量K, 带宽B, 多播组G 输出: 带宽约束下的最优值并将该方案写入数组X[J][l] 中 Output:X[J][l],f(K,B) (1)functionf(K,B) (2)Initializef(0,b)=0,k=0 (3)fork=1→Kdo (4)forb=1→Bdo (6)fork=1→Kdo (7)forb=1→Bdo (8)f(k,b)←f(k-1,b); (9)bk←0; (10)forb′=1→bdo (11) 代入动态规划模型的优化目标函数 (12)θmax←f(k-1,b-b′)+θk; (13) 将选择的最优方案写入数组X[J][l] 中 (14)ifθmax>f(k,b)then (15)f(k,b)←θmax; (16)X[J][l]=1; (17)else (18)X[J][l]=0; (19)returnX[J][l],f(K,B) (20)endfunction 算法1求出在带宽约束下的最优放置方案,将算法1输出的J个分层视频放置方案X[J][l] 带入到算法2中,使用函数f′(j,c) 表示前j个分层视频缓存方案的最大和PSNR。根据动态规划思想可得优化目标函数f′(j,c), 即 f′(j,c)=maxf(j-1,c-1)+θ′k (12) θ′k可以通过式P1得到,f′(j,c) 通过多项选择背包算法求解。把J个分层视频缓存方案当作J类物品,装入一个容量为C的背包中。每类有C个项目,第j类的第ck个项目有利润θ′k和重量ck。 那么f′(j,c) 的实质是从每个类别中选择一部分,不超出背包总容量,使利润总和最大。 算法设计使用动态规划方法,当所有项的权值为非负整数时,求出背包问题的最优解,即f′(j,c) 的最优解。首先,初始化f′(j,c)=0,j=0表示没有视频存在。然后,循环计算所有θ′k的值。接下来,从j=1开始递归地计算f′(j,c), 在递归的每次迭代中,使用递归式(12)计算f′(j,c), 其f′(j-1,c-c′) 在前一次递归迭代中已经计算过,θ′k在递归过程之前已经计算过。在JC次的迭代之后,可以获得了所有f′(j,c) 的值。最后,返回f′(J,C) 作为最优的系统PSNR。流程如算法2所示。 算法2: 多播组内分层内容缓存算法 输入:视频缓存方案J, 缓存C, 多播组G 输出:缓存约束下的最优值f′(J,C) Input:J,C,G={g1,g2,…gK} Output:f′(J,C) (1)functionf′(J,C) (2) Initializef′(0,c)=0,j=0 (3)forj=1→Jdo (4)forc=1→Cdo (6)forj=1→Jdo (7)forc=1→Cdo (8)f′(j,c)←f′(j-1,c); (9)ck←0; (10)forc′=1→Cdo (11) 代入动态规划模型的优化目标函数 (12)θ′max←f′(j-1,c-c′)+θ′k; (13)ifθ′max>f′(j,c)then (14)f′(j,c)←θ′max; (15)returnf′(J,C) (16)endfunction 利用大量的数据模拟来评估所提方案的性能。考虑一个半径为800 m的圆形覆盖区域的单元,各组用户在多播组内随机分布且分布均匀,基站的下行发射功率为40 dBm。对于信道传输模型,使用Lm(z)=-30-35log10(z) 来描述基站的下行信道增益[17],其中z为基站与用户设备之间的距离。缺省的参数见表3。 表3 仿真参数 使用文献[11]中挑选的SVC视频流的标准视频测试序列,并使用数据速率和PSNR值作为评价指标。表4给出了不同视频文件的每一层的数据速率和PSNR信息。 表4 评估中使用的可伸缩视频的数据速率(KBPS)和PSNR值/dB 评估本文所提出的面向NOMA无线视频多播的分层视频缓存和频谱分配方案。在该方案中有10个多播组请求不同的SVC视频流,每个多播组的用户设备均为15个。图2给出了NOMA层数对所提出的方案性能的影响。 图2 NOMA层数的影响 图2展示了在不同NOMA层数下的聚合速率和平均PSNR。可以看到,随着N的增加聚合速率以及用户平均PSNR也随之增加。但从N等于3开始,增加速率趋于不变。这是因为随着N的不断增加,带宽和缓存的资源消耗也随之不断增加,但功率资源有限,这就导致了当NOMA层数增加时,总累加率不会增加太多。另一方面,随着N的不断增加,缓存空间需求量必然增加,而基站的总缓存也是固定的,所以随着N的增加并不能显著提高性能甚至会出现“放不下”的情况。在仿真中,NOMA层数均设置为3,频率资源分配方法均采用基于动态规划的背包算法。 为了客观地评估性能,在考虑缓存约束的情况下实现了与两种基准方案的对比,包括: 可伸缩FPA-NOMA视频多播(SFNM)[14]:NOMA层的固定功率分配是一般基准,其中每个NOMA层的功率比例都是预先确定的。在这里,将SFNM扩展到能够多播SVC视频流的可扩展SFNM多播算法。首先,将该组均匀地划分为K个子组,并将这些子组顺序匹配到N个NOMA层。然后,从基础层到最高增强层的升序分配视频层。 可伸缩OMA视频多播(SOM)[16]:在SOM中,不同的视频层以不同的传输速率传输,不同的传输速率对于不同的信道增益是可以接受的。在该方案中,这些视频层通过正交的信道资源传输。 比较Proposed与两种方案的聚合速率和用户平均PSNR大小,如图3所示。可以看出,Proposed的聚合速率和用户平均PSNR最大,其次是SOM和SFNM。 图3 Proposed结果与两个基准方案的比较 在SFNM中,由于固定的子分组策略和固定的功率分配对终端的信道增益影响不明显,使其性能最差。SOM和Proposed,它们以最大化PSNR的方式进行调度。因为可扩展性是启用的,使用SOM和Proposed可以实现更好的性能。与SOM相比,Proposed以一种更有效的非正交方式利用资源。因此,它实现了最大的用户平均PSNR。 图4给出了10个视频在10~24个缓存区下,最优放置方案的分层视频缓存大小和最大传输速率的关系。如图4所示,分层视频缓存大小随着传输速率的增加不断递增。图中在不同分层视频缓存方案的情况下出现了传输速率相同的情况,这说明在不同缓存区中最大传输速率可能相同。这是因为每个视频的传输速率存在差异,见表4。 图4 聚合速率和缓存大小的关系 给定多播组的数量为10,每个多播组内的用户设备数为15个,系统缓存区数量为10~24(本文方案),子信道数量10~24。图5给出了3种方案随着子信道数量增加的变化趋势。3种方案分别为考虑缓存约束的Proposed方案和不考虑缓存约束的SOM方案和SFNM方案。 图5 缓存的影响 如图5所示,随着子信道数量的增加,所有方案的系统总PSNR值都有所提高,所提出的方案拥有最大系统总PSNR,其次是SOM和SFNM。原因是所提出方案基于动态规划方法可以更有效地在多组间分配资源,对资源进行充分的利用。当子信道数量足够大时,系统总PSNR增量减缓并逐渐趋于不变。这是因为随着子信道数量的增加,可以传输更多的分层缓存视频信息。 给定多播组数量为10,每个多播组内的用户设备数为15个,多播组的数量为4~10个。图6给出用户平均PSNR随着多播组数增加的变化趋势。 图6 多播组数的影响 在图6中,当用户组个数从4增加到6时,得益于基站间的频谱重用,所提出方案和SOM方案中分配给每一组的子信道不会减少,因此用户平均PSNR呈现增长的趋势。当多播组数量继续增加时,分配给每一组的子信道和缓存逐渐减少,因此每个用户设备的平均PSNR也在减少。当多播组数量在4~6个时,所提出方案的性能与SOM相差不大。随着多播组数量的增加,所提出方案在系统PSNR和用户平均PSNR 方面表现最好,其次是SOM和SFNM。 本文提出面向NOMA无线网络的分层视频内容缓存。在无线网络中,将NOMA与SVC视频多播相结合,研究了在带宽、功率、缓存的约束下多播资源的分配问题,以最大限度地提高多播组的整体视频质量。仿真结果表明,所提出的面向NOMA无线网络的视频内容缓存在系统PSNR和用户设备平均PSNR优于两种其它方案。下一步将采用缓存资源的预测,根据组内用户的偏好与习惯预先放置缓存视频资源,可以更进一步降低传输时延提升用户的视频体验。1.3 数据缓存
2 问题建模
2.1 无线频谱分配
2.2 功率分配
2.3 联合优化问题

3 问题近似与算法设计
3.1 问题分解


3.2 频谱管理算法
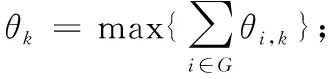
3.3 内容缓存算法
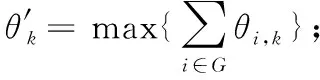
4 实验设计与结果分析
4.1 方案性能评估
4.2 缓存资源数量对性能的影响
4.3 多播组数量对性能的影响
5 结束语

